三维重建基础
目录
- 图像的高频信息和低频信息
- 旋转矩阵和平移向量
-
- 平移向量
- 旋转矩阵
- 相机成像中的四个坐标系
图像的高频信息和低频信息
低频信息指的是颜色缓慢变化,代表着连续渐变的一块区域,这部分为低频信息。对于一副图像来说,除去高频就是低频,也就是边缘以内的内容为低频,而边缘内的内容就是图像的大部分信息,即图像的大致概貌和轮廓,是图像的近似信息。
反之,图像边缘的灰度值变化快,就对应着高频。图像的细节处也就是属于灰度值急剧变化的区域,正是因为灰度值的急剧变化,才会出现细节。另外对于噪声,在一个像素所在的位置,之所以是噪点,是因为它与正常的点颜色不一样了,也就是说该像素点灰度值明显不一样,所以是高频部分。
通常,图像的低频是图像中对象的大致概况内容,高频对应噪声和细节。
ICML2018"On the spectral bias of neural networks"的研究指出,神经网络更倾向于拟合高频信息,而人类主要关注低频信息,然而对低频分量的学习,更有助于网络提高在对抗干扰过程中的鲁棒性。
旋转矩阵和平移向量
旋转矩阵和平移向量描述了一个刚体在三维空间中的运动状态。
平移向量
首先了解平移向量:
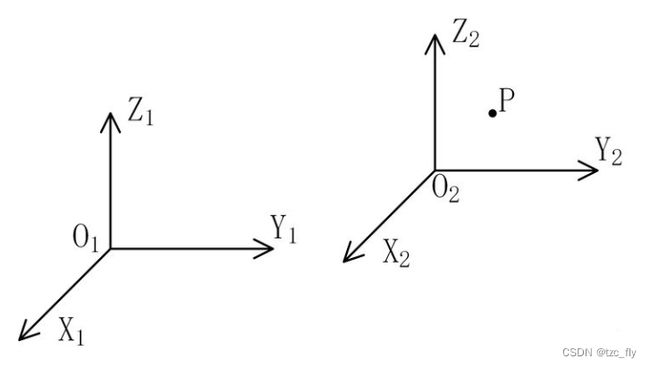
坐标系1和坐标系2平行但不重合,所以空间点从坐标系2到坐标系1的变换只有平移向量,用 t t t表示。假设,坐标系2的原点 O 2 O_{2} O2在坐标系1中为 ( X O 2 , Y O 2 , Z O 2 ) (X_{O_{2}},Y_{O_{2}},Z_{O_{2}}) (XO2,YO2,ZO2),空间点 P P P在坐标系2中的坐标为 ( X 2 , Y 2 , Z 2 ) (X_{2},Y_{2},Z_{2}) (X2,Y2,Z2),则点 P P P在坐标系1中的坐标 ( X 1 , Y 1 , Z 1 ) (X_{1},Y_{1},Z_{1}) (X1,Y1,Z1)为: X 1 = X 2 + X O 2 X_{1}=X_{2}+X_{O_{2}} X1=X2+XO2 Y 1 = Y 2 + Y O 2 Y_{1}=Y_{2}+Y_{O_{2}} Y1=Y2+YO2 Z 1 = Z 2 + Z O 2 Z_{1}=Z_{2}+Z_{O_{2}} Z1=Z2+ZO2即空间点从坐标系2到坐标系1的变换可以表示为: P 1 = P 2 + t P_{1}=P_{2}+t P1=P2+t;
其中, P 1 P_1 P1、 P 2 P_2 P2分别为空间点 P P P在坐标系1和坐标系2中的坐标, t t t为空间点从坐标系2变换到坐标系1的平移向量。
旋转矩阵
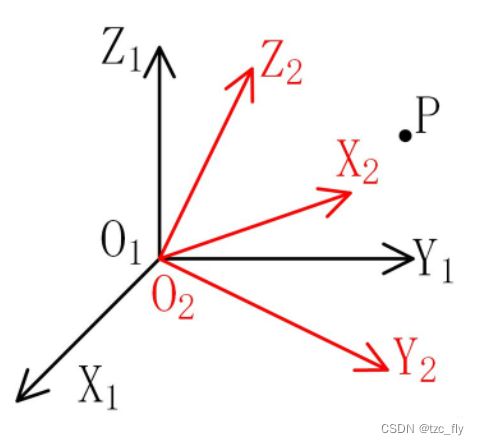
如图,坐标系1和坐标系2原点重合但是不平行,所以空间点从坐标系2到坐标系1的变换只有旋转矩阵,用 R R R表示。空间点 P P P在坐标系1和坐标系2中的坐标分别为 P 1 P_1 P1、 P 2 P_2 P2,则: P 1 = R P 2 P_{1}=RP_{2} P1=RP2其中,旋转矩阵为:

令:
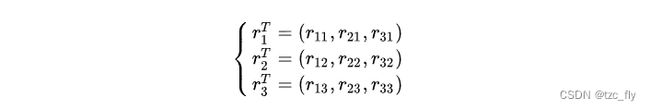
则: R = ( r 1 , r 2 , r 3 ) R=(r_1,r_2,r_3) R=(r1,r2,r3),在坐标系2中取三个点 A ( 1 , 0 , 0 ) , B ( 0 , 1 , 0 ) , C ( 0 , 0 , 1 ) A(1,0,0),B(0,1,0),C(0,0,1) A(1,0,0),B(0,1,0),C(0,0,1),分别将其转换到坐标系1中,则:
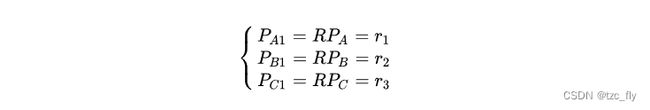
即,空间点从坐标系2到坐标系1的旋转矩阵 R R R的分量 r 1 , r 2 , r 3 r_1,r_2,r_3 r1,r2,r3分别为坐标系2的基底向量在坐标系1中的表示。
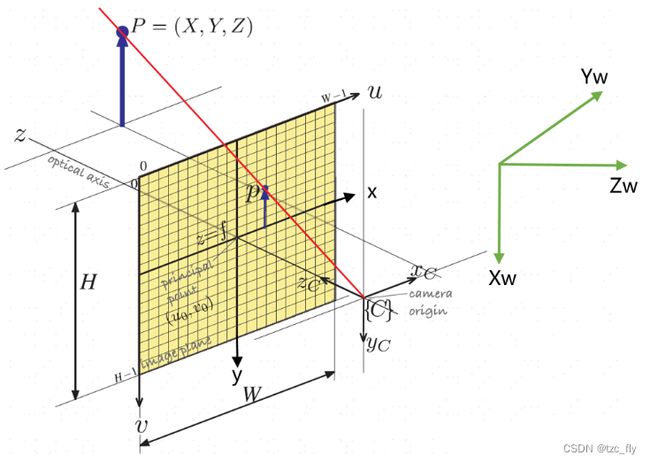
相机成像中的四个坐标系
- 图像像素坐标系:表示三维空间物体在图像平面(上图黄色的image plane)上的投影,像素是离散化的,其坐标原点在图像平面的左上角。 u u u轴平行于图像平面水平向右, v v v轴垂直于 u u u轴向下,坐标用 ( u , v ) (u,v) (u,v)表示,图像宽 W W W,高 H H H。
- 图像物理坐标系:坐标原点在图像平面中心, x , y x,y x,y轴分别平行于图像像素坐标系的 u , v u,v u,v轴,坐标用 ( x , y ) (x,y) (x,y)表示。
- 相机坐标系:以相机的光心(camera origin)为坐标系原点, x C , y C x_{C},y_{C} xC,yC
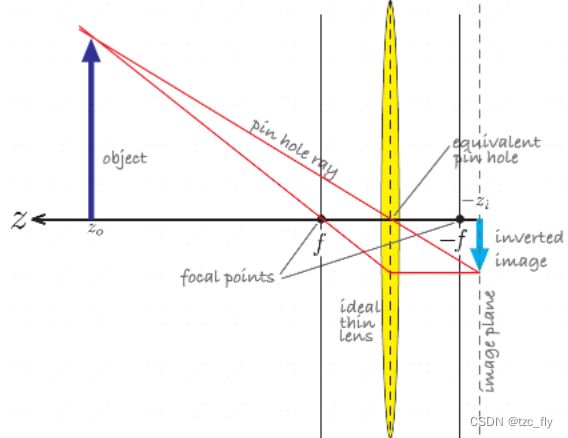
轴平行于图像物理坐标系的 x , y x,y x,y轴,相机的光轴为 z C z_{C} zC轴,坐标系满足右手法则。相机的光心可以理解为相机透镜的几何中心,如下图所示,物理成像平面和光心的距离为 f f f(即为焦距)。
- 世界坐标系:用于表示空间物体的绝对坐标,使用 ( X w , Y w , Z w ) (X_{w},Y_{w},Z_{w}) (Xw,Yw,Zw)表示,世界坐标系可通过旋转和平移对应到相机坐标系。
基于四个坐标系,我们记 P u v = ( u , v , 1 ) T P_{uv}=(u,v,1)^{T} Puv=(u,v,1)T为图像像素坐标系下的某个像素的坐标, P = ( x C , y C , z C ) P=(x_{C},y_{C},z_{C}) P=(xC,yC,zC)为其对应的相机坐标系下的坐标,两者具有以下关系: P u v = 1 z C K P → z C P u v = K P P_{uv}=\frac{1}{z_{C}}KP\rightarrow z_{C}P_{uv}=KP Puv=zC1KP→zCPuv=KP其中, z C P u , v ∈ R 3 × 1 z_{C}P_{u,v}\in R^{3\times 1} zCPu,v∈R3×1, K K K为:

即相机内参,相机内参一般都是相机出厂就定下来的,也可以通过相机标定的方式人为计算出来。
令 P w ∈ R 3 × 1 P_{w}\in R^{3\times 1} Pw∈R3×1为该像素对应的世界坐标系下的坐标,我们有: P = R P w + t P=RP_{w}+t P=RPw+t z C P u , v = K ( R P w + t ) z_{C}P_{u,v}=K(RP_{w}+t) zCPu,v=K(RPw+t)其中, R R R和 t t t是相机外参,决定了相机的位姿。
注意到, P P P对应前面所说的旋转矩阵和平移向量的坐标系1, P w P_{w} Pw对应坐标系2。
相机内参:从相机坐标系转换到像素坐标系;
相机外参:从世界坐标系转换到相机坐标系;