数字图像处理——第九章 形态学处理
文章目录
- 引言
- 9.1 一些基本的形态学集合
- 9.2 腐蚀和膨胀
- 9.3 开操作与闭操作
- 9.4 击中与击不中
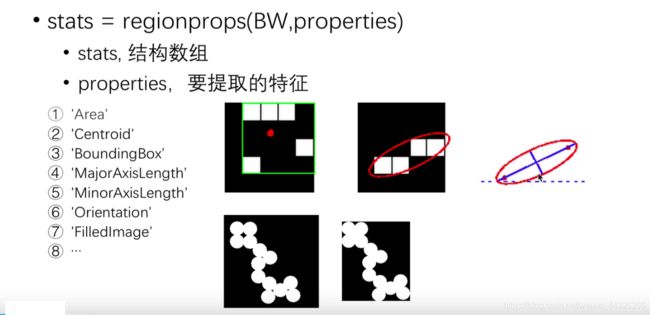
- 9.5 形态学处理函数
- 实验部分
- 总结
引言
本章主要将数学形态学作为工具从图像中提取表达和描绘区域形状的有用图像分量,如边界、骨架和突壳等。我们对预处理或后处理的形态学技术也感兴趣,比如形态学过滤、细化和修剪等。
我们主要处理步骤如下:首先对图像进行二值化处理,接着做连接成分的变形,包括图像的测量和结构的分析。
9.1 一些基本的形态学集合
在二值图像中,所有白色像素或黑色像素的集合是二维整数空间 Z 2 Z^2 Z2的成员,在该空间中,集合的每个元素都是一个多元组(二维向量),也就是像素的坐标(x,y),而灰度图像可以表示为在空间 Z 3 Z^3 Z3中的集合,第三个分量对应于其离散灰度值。
集合1:
B = [ w ∣ w = d , d ∈ D ] B=[w|w=d,d\in D] B=[w∣w=d,d∈D]所表达的意思是集合B是元素w的集合,而w是通过1与集合D中所有的元素相乘得到的,即令集合的元素为图像中表示区域(物体)的像素的坐标。
集合2:(集合1的反射)
B ^ = [ w ∣ w = − d , d ∈ D ] \hat{B}=[w|w=-d,d\in D] B^=[w∣w=−d,d∈D] B ^ \hat{B} B^是B中(x,y)坐标被(-x,-y)替代的点的集合。
集合3:(集合1的平移)
( B ) z = [ c ∣ c = b + z , d ∈ B ] (B)_z=[c|c=b+z,d\in B] (B)z=[c∣c=b+z,d∈B]集合B按照点z( z 1 z_1 z1, z 2 z_2 z2)的平移,表示为 ( B ) z (B)_z (B)z 。
形态学中的集合的反射和平移广泛用来表达基于结构元(struct element)的操作:研究一幅图像中感兴趣特性所用的小集合或子图像,用涂阴影的方块表示SE的一个成员,且我们必须指定SE的原点。
对图像操作时,要求SE是矩形阵列。且计算机实现要求用添加背景的方法把背景也转换为一个矩形阵列,背景边界要大到足以容纳整个结构元,类似于空间相关的和卷积的填充操作。
假定定义一个结构元在集合A上的操作如下:B的原点访问A的每个元素,若在B的每个原点位置,完全被A包含,则将该位置标记为新集合的一个成员,反之不成立。
9.2 腐蚀和膨胀
腐蚀:
作用:消除边界点,使边界向内部收缩,用来消除小且无意义的物体。
定义1: A ㊀ B = [ z ∣ ( B ) z ∈ A ] A㊀B=[z|(B)_z \in A] A㊀B=[z∣(B)z∈A]表明A一定要完全包含B的移动区域
定义2: A ㊀ B = [ z ∣ ( B ) z ∩ A c = ∅ ] A㊀B=[z|(B)_z \cap A^{c}=\varnothing] A㊀B=[z∣(B)z∩Ac=∅]表达B的移动区域与A的补集是空集。
当B以原点为参考对象,遍历至A的背景时,若未完全包含B,则不能成为新的集合,即被“腐蚀”。
当背景图内部有空洞(hollow)时,这个洞的区域将会变大。
如图所示:

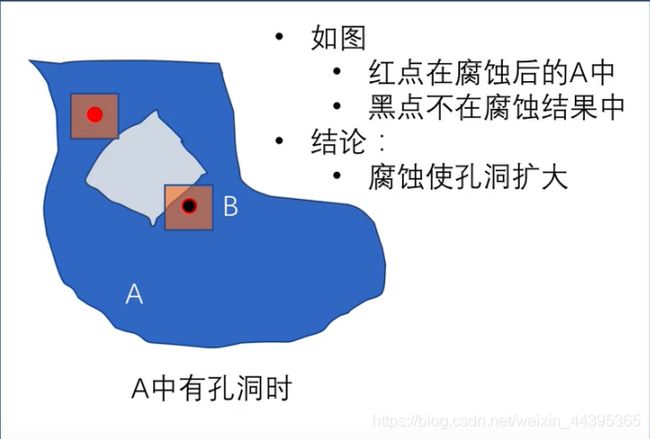
来看一个应用,用不同直径的圆(元素为1,即为白色),来腐蚀焊接的白色区域:

随着半径越来越大,白色部分包含不了全部的SE,则白色的部分被腐蚀,中心最大的矩形也小了一圈。
腐蚀函数:erode(img,SE)
膨胀:
作用:加长或变粗二值图像中的对象
定义1:
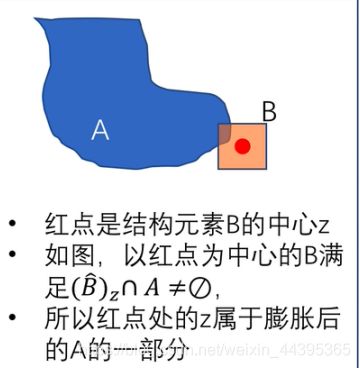
A ⨁ B = [ z ∣ ( B ^ ) z ∩ A ≠ ∅ ] A\bigoplus B=[z|(\hat{B})_z \cap A \neq \varnothing] A⨁B=[z∣(B^)z∩A=∅]
即B的反射经过平移与A的交集不是空集,有交集即可算作新的集合。
定义2:
A ⨁ B = [ z ∣ ( B ^ z ∩ A ∈ A ) ] A\bigoplus B=[z|(\hat{B}_{z} \cap A \in A)] A⨁B=[z∣(B^z∩A∈A)]
即B的反射率经过平移与A的交集是A的子集。
两张图片说明膨胀的功能:

简单的膨胀应用是连接裂缝,函数是imdiate(img,SE)。
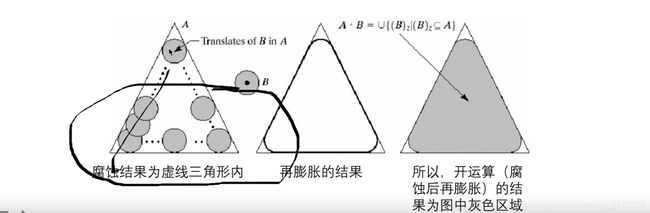
9.3 开操作与闭操作
开操作和闭操作是腐蚀和膨胀的运算结果。
开运算定义(先腐蚀再膨胀):
A 。 = ( A ㊀ B ) ⨁ B A^{。}=(A㊀B)\bigoplus B A。=(A㊀B)⨁B
开运算作用:
- 删除不能包含结构元素的对象
- 平滑轮廓
- 断开狭窄的连接
- 消除细的突出物
几何解释:首先先经过腐蚀使尖锐的部分变得平滑,并使图像缩小,接着膨胀,图形保持形状而扩大区域。
函数:imopen(img,SE)
闭运算定义(先膨胀再腐蚀):
A ⋅ B = ( A ⨁ B ) ㊀ B A\cdot B=(A\bigoplus B)㊀B A⋅B=(A⨁B)㊀B
作用
- 平滑对象轮廓
- 将狭窄的缺口连接起来
- 填充比结构元素小的洞
- 填补轮廓线的断裂
函数:imclose(img,SE)
以图为例,作对照:


当然,我们也可对开闭运算进行计算。
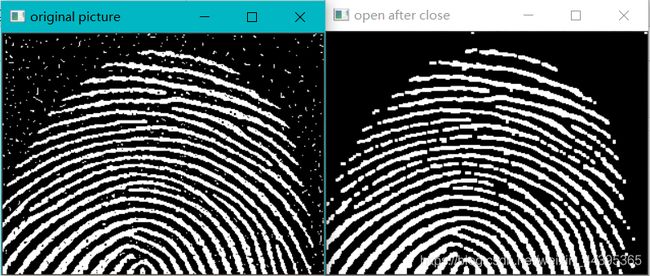
比如,在指纹这张图中,可以观察到存在着噪声,可以当作细小的部分,经过开运算时候,去除了噪声(腐蚀阶段),但指纹的间隙变大了,我们再经过闭运算,可将部分指纹的间隙给连接。

与腐蚀和膨胀的‘单’运算结果肯定不一样,因为膨胀的结果是加粗,并不会使断线连接。
9.4 击中与击不中
运算定义: A ⨂ B = ( A ㊀ B 1 ) ∩ ( A C ㊀ B 2 ) A \bigotimes B= (A㊀B_{1}) \cap(A^{C}㊀B_{2}) A⨂B=(A㊀B1)∩(AC㊀B2)
B 1 B_{1} B1用于探测图像内部,作为击中部分; B 2 B_{2} B2 用于检测图像外部,作为击中部分,二者之间没有交集。
要点:
- 可利用腐蚀来确定目标的位置
- 检测要同时捕获内外标记
- B={ B 1 , B 2 B_1, B_2 B1,B2},即检测元素有两个
用张图简要表示一下作用:

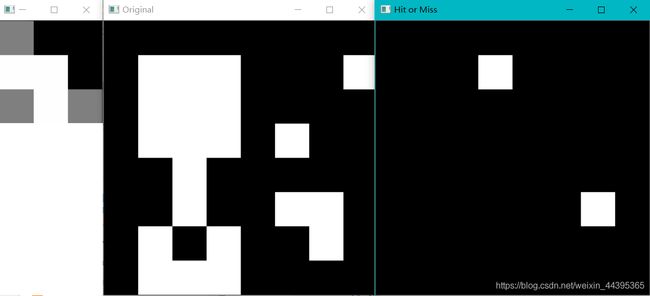
击中的意义是存在这样的结构元素的原点,这个点在背景中,即在背景中存在结构元素的形状,上图的计算结果的黑点即是结构元素的原点,也就是击中了。
再来看一个例子:击中击不中的示意图

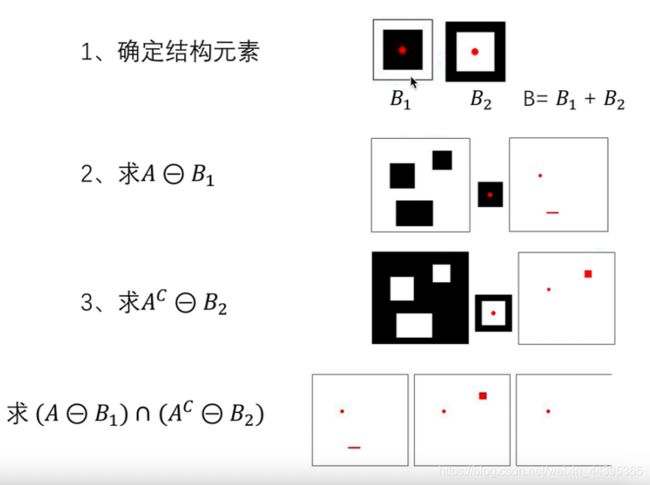
函数:bwhitmis(BW1,SE1,SE2),SE2=1-SE1
公式:imerode(BW1,SE1)&imerode(-BW1,SE2)
9.5 形态学处理函数
实验部分
定义结构元素
# 定义SE
SE=np.ones((11,11),np.uint8)
# 定义十字型的SE
SE=np.zeros((11,11))
SE[5,0:11]=SE[0:11,5]=1
print(SE)
SE=np.zeros((11,11))
row,col=SE.shape
for i in range(row):
for j in range(col):
SE[5,j]=SE[i,5]=1
print(SE)
#使用cv.getStructringElement函数
SE = cv.getStructuringElement(cv.MORPH_CROSS,(11,11),(5,5))
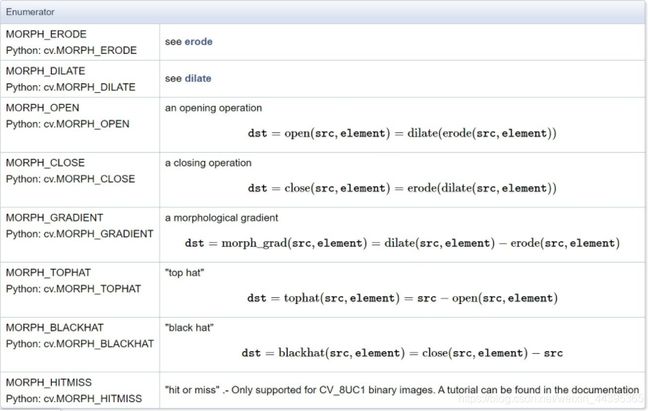
# Morph命令
dst =cv.morphologyEx(src, op, kernel[, dst[, anchor[, iterations[, borderType[, borderValue]]]]] )
腐蚀:
SE1 = cv.getStructuringElement(cv.MORPH_RECT,(11,11))
SE2 = cv.getStructuringElement(cv.MORPH_RECT,(15,15))
SE3 = cv.getStructuringElement(cv.MORPH_RECT,(45,45))
img=cv.imread('pic/hanjiepan.tif')
img_erode1=cv.erode(img,SE1)
img_erode2=cv.erode(img,SE2)
img_erode3=cv.erode(img,SE3)
cv.imshow('erode effect1',img_erode1)
cv.imshow('erode effect2',img_erode2)
cv.imshow('erode effect3',img_erode3)
cv.waitKey(0)
cv.destroyAllWindows
结果如图所示,随着结构元素的区域越来越大,焊接盘上的白色区域逐渐被腐蚀,最后一个中心的白色区域也被部分腐蚀。
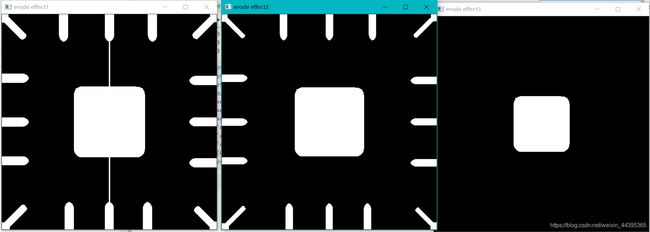
膨胀:
img02=cv.imread('pic/wenzi.tif')
SE = cv.getStructuringElement(cv.MORPH_CROSS,(3,3))
img_dilate=cv.dilate(img02,SE)
cv.imshow('erode effect1',img_dilate)
cv.imshow('original picture',img02)
cv.waitKey(0)
cv.destroyAllWindows
结果如图所示,文字轮廓变粗,断线也被部分修补填充。

先开后闭:
img = cv.imread('pic/zhiwen.tif')
SE = cv.getStructuringElement(cv.MORPH_RECT,(3,3 ))
img_opened = cv.morphologyEx(img, cv.MORPH_OPEN, SE)
img_closed_opened = cv.morphologyEx(img_opened, cv.MORPH_CLOSE, SE)
cv.imshow('original picture',img)
cv.imshow('close after open', img_closed_opened)
cv.waitKey(0)
cv.destroyAllWindows()
结果如图所示:
经过开运算时候,去除了噪声(腐蚀阶段),但指纹的间隙变大了,我们再经过闭运算,可将部分指纹的间隙给连接。
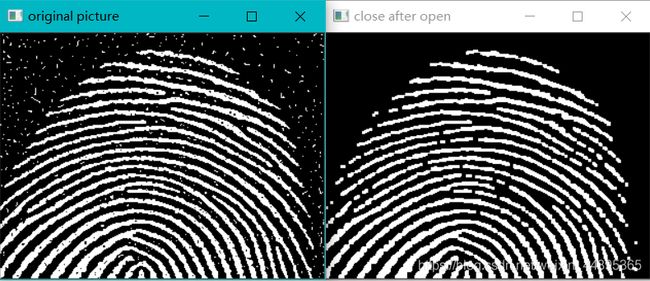
先闭后开:结果图与第一张对比,可以观察到,最上面有个噪声没有被去除,第一行,第二行的断线没有第一张填补得充分。
hit or miss:
import cv2 as cv
import numpy as np
input_image = np.array((
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 255, 255, 255, 0, 0, 0, 255],
[0, 255, 255, 255, 0, 0, 0, 0],
[0, 255, 255, 255, 0, 255, 0, 0],
[0, 0, 255, 0, 0, 0, 0, 0],
[0, 0, 255, 0, 0, 255, 255, 0],
[0,255, 0, 255, 0, 0, 255, 0],
[0, 255, 255, 255, 0, 0, 0, 0]), dtype="uint8")
kernel = np.array((
[0, -1, -1],
[1, 1, -1],
[0, 1, 0]), dtype="int")
output_image = cv.morphologyEx(input_image, cv.MORPH_HITMISS, kernel)
rate = 50
kernel = (kernel + 1) * 127
kernel = np.uint8(kernel)
kernel = cv.resize(kernel, None, fx = rate, fy = rate, interpolation = cv.INTER_NEAREST)
cv.imshow("kernel", kernel)
# x、y反向扩大50倍
input_image = cv.resize(input_image, None, fx = rate, fy = rate, interpolation = cv.INTER_NEAREST)
cv.imshow("Original", input_image)
output_image = cv.resize(output_image, None , fx = rate, fy = rate, interpolation = cv.INTER_NEAREST)
cv.imshow("Hit or Miss", output_image)
cv.waitKey(0)
cv.destroyAllWindows()
第三张图白色区域即为击中区域。
形态学梯度:
定义: g = ( f ⨁ B ) − ( f ㊀ B ) g=(f\bigoplus B)-(f㊀B) g=(f⨁B)−(f㊀B)
img03=cv.imread('pic/skull.tif')
SE=cv.getStructuringElement(cv.MORPH_RECT,(3,3))
img_grad=cv.morphologyEx(img_opened, cv.MORPH_GRADIENT, SE)
cv.imshow('skull',img03)
cv.imshow('tidu',img_grad)
cv.waitKey(0)
cv.detroyAllWindows()
结果表明:梯度处理后达到微分的效果,提取了边界信息。

形态学重构:
#主要代码
gray_A = cv2.cvtColor(img_A, cv2.COLOR_BGR2GRAY) #转换成灰度图
ret, thresh_A = cv2.threshold(gray_A, 50, 255, cv2.THRESH_BINARY_INV) #灰度图转换成二值图像
thresh_A_copy = thresh_A.copy() #复制thresh_A到thresh_A_copy
thresh_B = np.zeros(gray_A.shape, np.uint8) #thresh_B大小与A相同,像素值为0
kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (3,3))#3×3结构元
count = [ ] #为了记录连通分量中的像素个数
#循环,直到thresh_A_copy中的像素值全部为0
while thresh_A_copy.any():
Xa_copy, Ya_copy = np.where(thresh_A_copy > 0) #thresh_A_copy中值为255的像素的坐标
thresh_B[Xa_copy[0]][Ya_copy[0]] = 255 #选取第一个点,并将thresh_B中对应像素值改为255
#连通分量算法,先对thresh_B进行膨胀,再和thresh_A执行and操作(取交集)
for i in range(200):
dilation_B = cv2.dilate(thresh_B, kernel, iterations=1)
thresh_B = cv2.bitwise_and(thresh_A, dilation_B)
#取thresh_B值为255的像素坐标,并将thresh_A_copy中对应坐标像素值变为0
Xb, Yb = np.where(thresh_B > 0)
thresh_A_copy[Xb, Yb] = 0
#显示连通分量及其包含像素数量
count.append(len(Xb))
if len(count) == 0:
print("无连通分量")
if len(count) == 1:
print("第1个连通分量为{}".format(count[0]))
if len(count) >= 2:
print("第{}个连通分量为{}".format(len(count), count[-1] - count[-2]))
总结
本章基于集合论基础,以形态学概念和技术作为从图像中提取感兴趣特征的有力工具,形态学可作为广泛应用分割程序的基础,在图像描述中也起着重要的作用。