【数据结构】二叉树 —— 浅_刷 - OJ练习题

前言

• 二叉树初期学习中最重要的是二叉树的遍历过程 —— 递归
• 递归这中最重要的思想便是分治的思想

前情回顾：
二叉树的遍历以及递归的分治思想： 传送门

本篇博客将接着上文继续带来一种遍历二叉树的方法 —— 层序遍历，并一起领略一下二叉树的OJ题，话不多说，准备启航！

---

1. 层序遍历

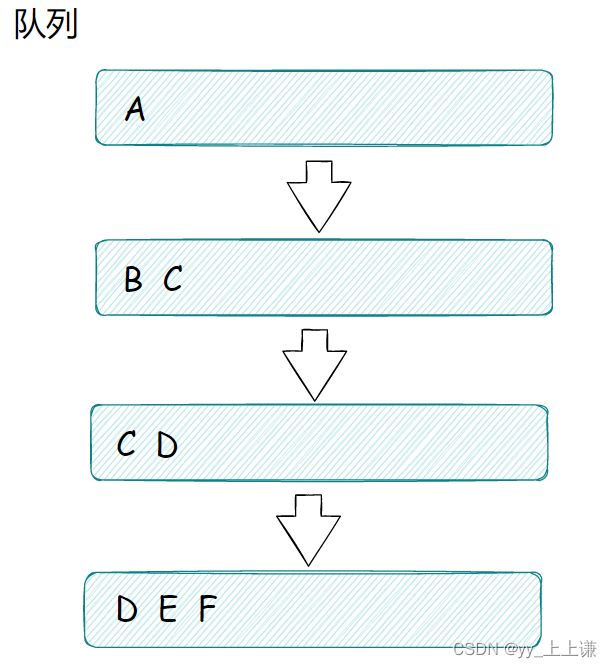
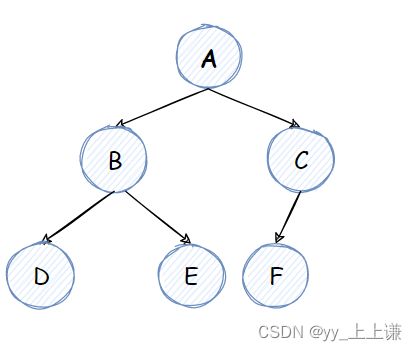
所谓层序遍历就是按照层数，将二叉树一层一层的遍历。

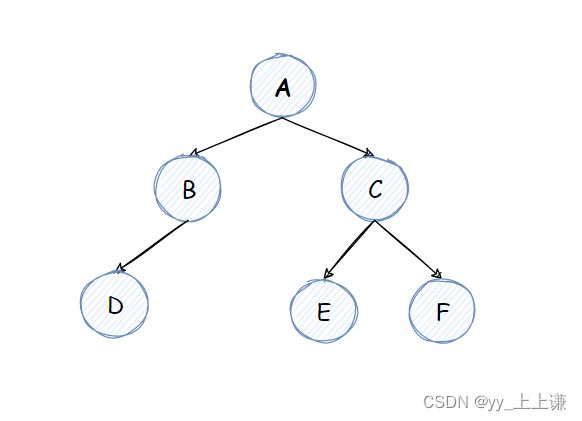
层序遍历的结果为：A B C D E F
那么我们该如何实现层序遍历呢：

• 这里我们没有用到递归的思想，因为是一层一层顺序遍历，所以我们首先想到的就是之前学到的一个数据结构 —— 队列。

队列不熟悉的小伙伴点这里： 传送门

思想：

• 利用队列先进先出的性质，我们先将根节点入队
• 只要有一个结点出队(该结点的指针不为空)，就该结点的两个孩子入队
• 打印出队结点的值
• 这样就将二叉树一层一层的遍历完了

注意：
我们这里入队的不是结点的值，因为我们还要将结点的孩子带到队列中去，所以我们这里入队的是结点 或 结点的指针，很显然入结点的指针更好，因为它占用的空间很小。
这时候我们当时实现队列的时候对数据类型重命名的优势就显现出来了：

• 我们只需要修改：“typedef struct BinaryTreeNode* QDataType;”这一句代码
• 后面用到的类型就全部变成结点指针类型的了
  

//二叉树的层序遍历
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);

	//根先进队列printf()
	if (root)
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		printf("%d ", front->data);

		if (front->left)
		{
			QueuePush(&q, front->left);
		}

		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}

	printf("\n");
	QueueDestroy(&q);
}

---

2. 判断二叉树是否是完全二叉树

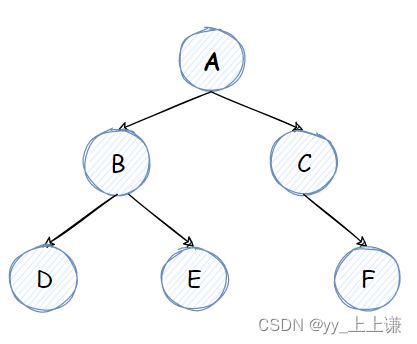
完全二叉树有个特性，它的前 k - 1 层是满二叉树，最后一层是连续的。

如图便是一个完全二叉树：

非完全二叉树：

这里我们还是用到了刚刚层序遍历的思想，还是用到了队列这个结构。

思想：

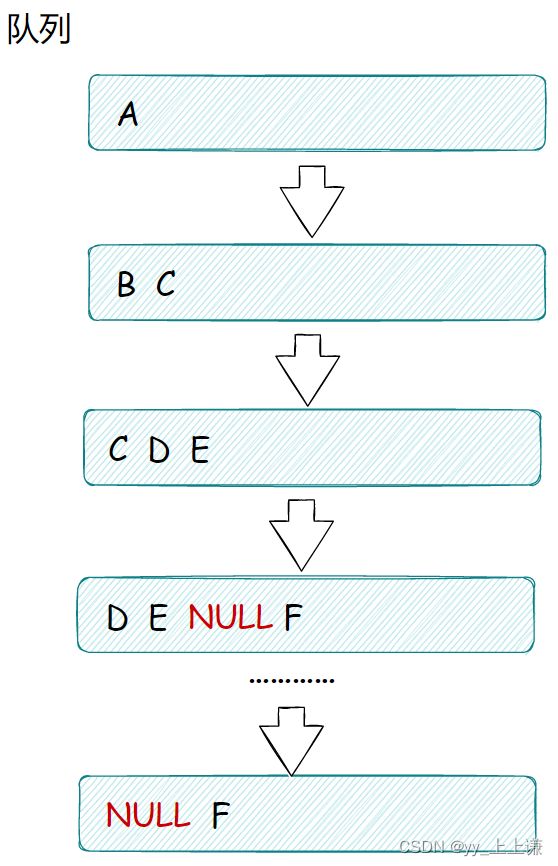
• 我们用刚刚层序遍历的思想，一层一层将结点入队，这个时候我们空结点也入队
• 在层序遍历的过程中，如果出队时出到了空，就停下来不再继续入队
• 我们对队列中剩下的元素进行挨个出队
• 如果全是空，说明是完全二叉树
• 如果此时出队的结点中有非空，说明不是完全二叉树

以非完全二叉树为例：

//判断二叉树是否是完全二叉树
bool BTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);

	//根先进队列printf()
	if (root)
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			break;
		}

		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//如果空后面出到非空，那么说明不是完全二叉树
		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	
	//循环结束，说明全是空并且出完了
	//此时就是完全二叉树
	
	QueueDestroy(&q);
	return true;
}

3. 还原二叉树

3.1 例题1：

二叉树的题目中还有一类比较重要的题目，那就是二叉树的还原。
题目会给出二叉树的前序遍历和中序遍历，或者后序遍历和中序遍历，根据条件将二叉树还原出来。

看例题：

已知某二叉树的前序遍历序列为ABDEC，中序遍历序列为BDEAC，则该二叉树（ ）

A.是满二叉树
B.是完全二叉树，不是满二叉树
C.不是完全二叉树
D.是所有的结点都没有右子树的二叉树

根据二叉树各个遍历的特性:

• 前序遍历 : - (先根遍历):根节点，左子树，右子树

• 中序遍历 : 左子树， 根节点， 右子树

• 后序遍历 : - (后跟遍历): 左子树，右子树，根节点

• 层序遍历 : 一层一层遍历

下面来说一下这题的思路:

• 根据前序遍历的性质(根左右)，那么根一定是在前面
• 找到根之后在中序遍历结果中可以将树分成左子树和右子树
• 再重复前两步，将左右子树划分成根左子树和右子树
• 直到不能再分割出子树
  
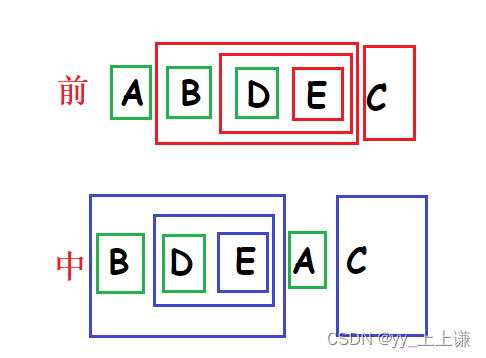
  还原后的树：
  
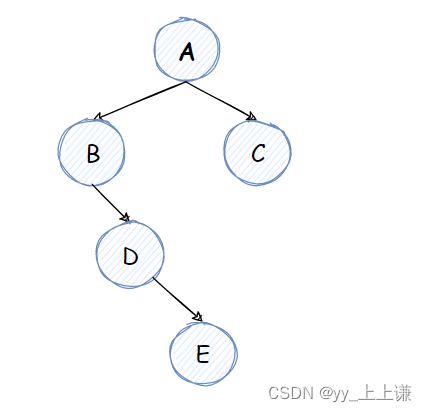
  所以本题选C：

3.2 例题2：

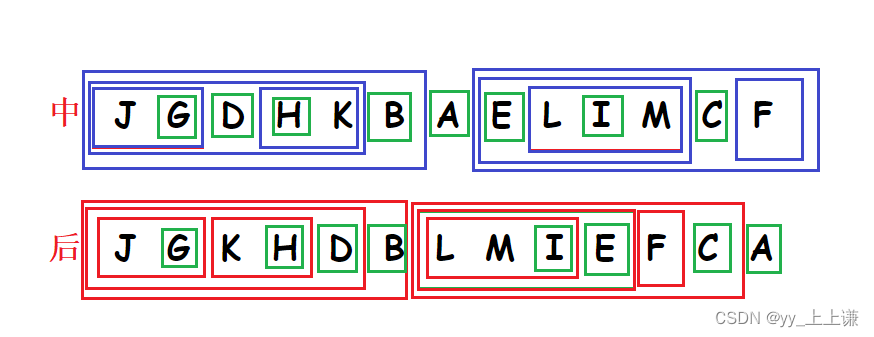
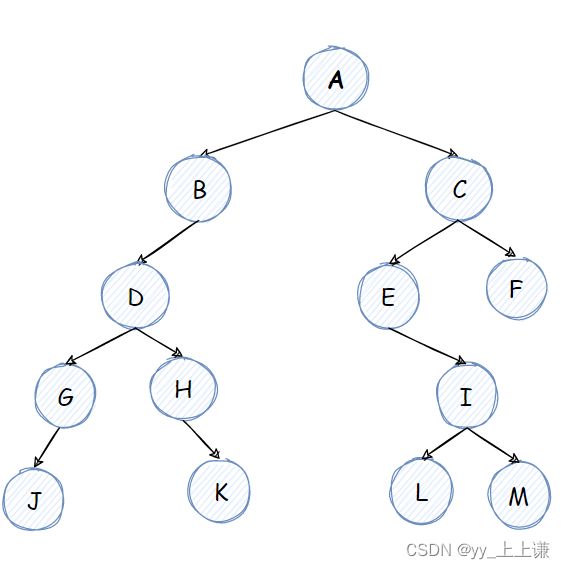
12.已知某二叉树的中序遍历序列为JGDHKBAELIMCF，后序遍历序列为JGKHDBLMIEFCA，则其前序遍历序列为（）

A.ABDGHJKCEFILM
B.ABDGJHKCEILMF
C.ABDHKGJCEILMF
D.ABDGJHKCEIMLF

还原后的树：

所以前序遍历为：A B D G J H K C E I L M F
故选 B

---

4. 二叉树OJ题

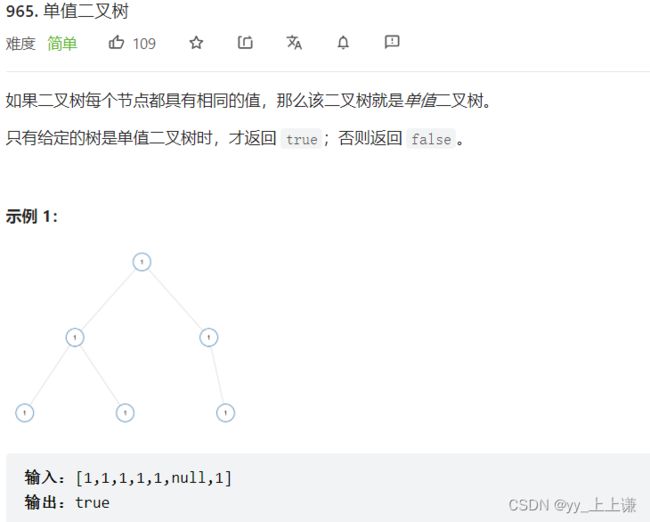
4.1 单指二叉树：

OJ链接

思想：

• 本质是一个前序遍历
• 空数也符合题意
• 先判断根是否 == val，再去判断左子树
• 只要不相等就返回假
• 遍历到最后叶子结点的时候返回真
• 左树遍历完之后再去遍历右树
• 只要左右两棵子树都为真才返回真

bool isUnivalTree(struct TreeNode* root)
{
    if(root == NULL)
    {
        return true;
    }
    
    if(root->left && root->left->val != root->val)
    {
        return false;
    }   
    if(root->right && root->right->val != root->val)
    {
        return false;
    }
    
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

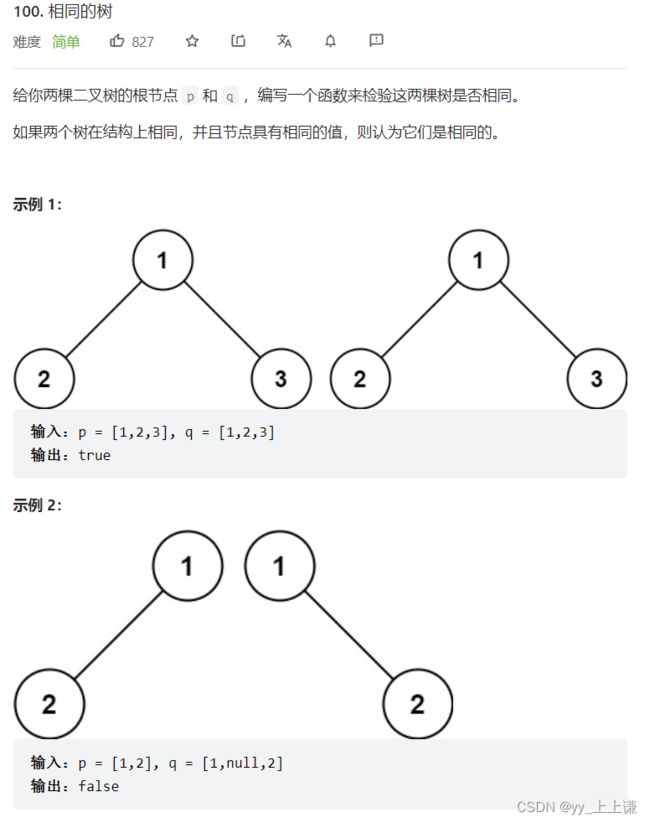
4.2 相同的树

OJ链接

思想：

• 两棵树分别开始遍历
• 都为空树为真
• 对应的一个为空，一个结点不为空返回假
• 若两个结点对应的值相同，继续向下遍历
• 同样是类似于一个前序遍历
• 根比较完了之后，再去比较左右子树

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if(p == NULL && q == NULL)
    {
        return true;
    }
    if(p == NULL || q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }

    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

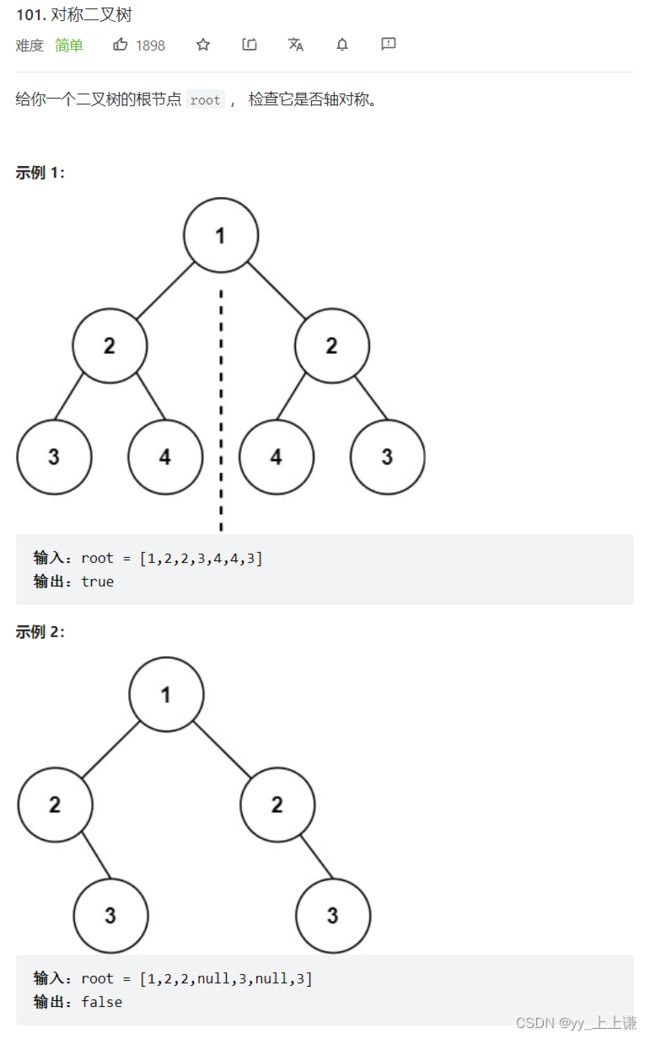
4.3 对称二叉树

OJ链接

思想：

• 对称二叉树又叫镜像二叉树
• 既然它们是左右对称的
• 那么左右子树一定是相同的，只是对应的值是相反的
• 我们可以巧妙改一下刚刚写的判断相同二叉树
• 去除根之后，比较两个子树是否相同
• 只需要改动“isSameTree(p->left, q->left) && isSameTree(p->right, q->right)“即可。

bool _isSymmetric(struct TreeNode* p, struct TreeNode* q)
{
    if(q == NULL && p == NULL)
    {
        return true;
    }
    if(q == NULL || p == NULL)
    {
        return false;
    }
    if(q->val != p->val)
    {
        return false;
    }

    return _isSymmetric(p->left, q->right) && _isSymmetric(p->right, q->left);
}

bool isSymmetric(struct TreeNode* root)
{
    if(root == NULL)
    {
        return true;
    }

    return _isSymmetric(root->left, root->right);
}

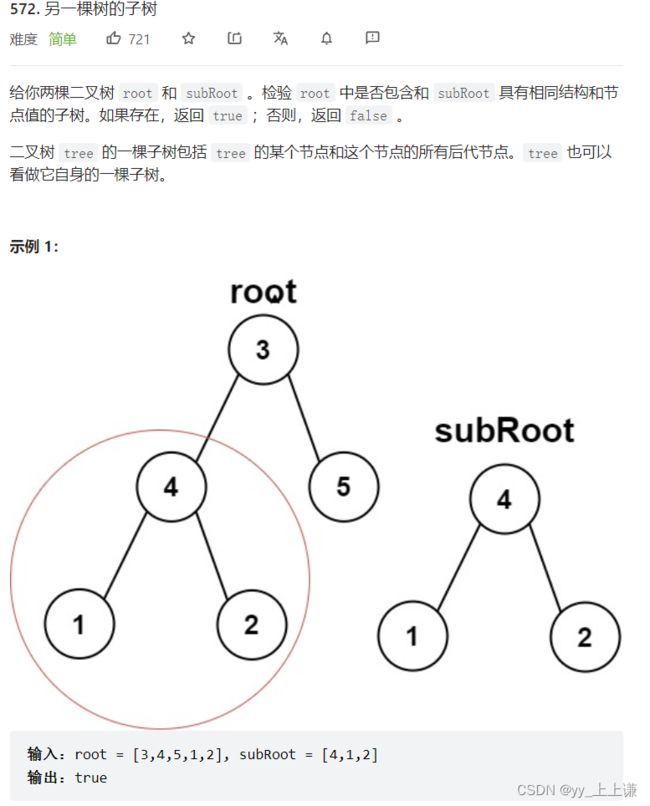
4.4 另一棵树的子树

OJ链接

思想：

• 遍历root树
• 每个结点都和subRoot树比一下，看是否相同
• 相同就返回真，不同就一直往下遍历
• 直到将root树遍历结束

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if(p == NULL && q == NULL)
    {
        return true;
    }

    if(p == NULL || q == NULL)
    {
        return false;
    }

    if(p->val != q->val)
    {
        return false;
    }

    return isSameTree(p->left,q->left) && isSameTree(p->right, q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if(root == NULL && subRoot == NULL)
   {
       return true;
   }
   if(root == NULL && subRoot != NULL)
   {
       return false;
   }

    return isSameTree(root,subRoot)
    || isSubtree(root->left,subRoot)
    || isSubtree(root->right,subRoot);
}

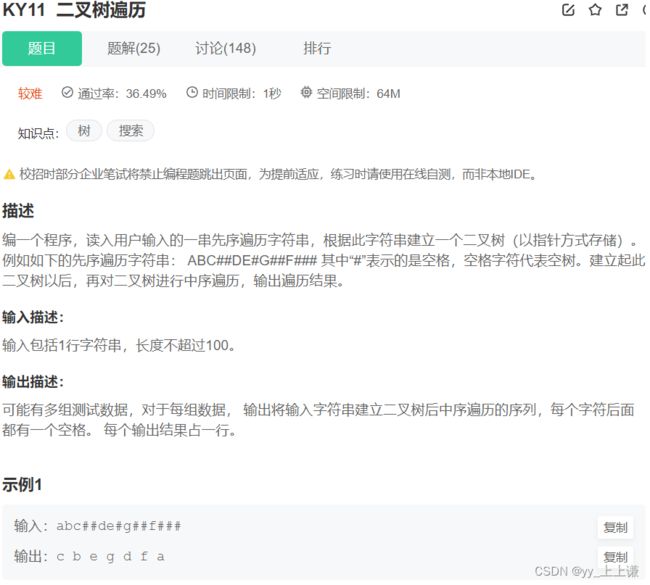
4.5 二叉树的构建及遍历

OJ链接

思想：

• 这题最主要的是创建二叉树
• 根据数组的内容而 前序遍历 的结果
• 那么创建二叉树的时候也需要以前序的顺序创建结点
• 具体看代码实现
• 前面的递归题搞懂之后，这里的建树会很好理解

#include
#include

typedef struct TreeNode
{
    struct TreeNode* left;
    struct TreeNode* right;
    char data;
}BTNode;

BTNode* CreatTree(char* arr, int* pi)
{
    if(arr[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    root->data = arr[(*pi)++];
    
    root->left = CreatTree(arr, pi);
    root->right = CreatTree(arr, pi);
    
    return root;
}

void InOrder(BTNode* root)
{
    if(root == NULL)
    {
        return;
    }
    
    InOrder(root->left);
    printf("%c ",root->data);
    InOrder(root->right);
}

int main()
{
    char arr[100];
    memset(arr, 0, sizeof(char) * 100);
    scanf("%s", arr);
    int i = 0;
    
    BTNode* root = CreatTree(arr, &i);
    InOrder(root);
    
    return 0;
}