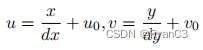深入浅出了解相机标定
文章目录
- 前言
- 相机标定
-
- 坐标系
-
- 坐标系转换
- 畸变与畸变校正
- 张氏标定法
- 参考
前言
最近的工作需要跟摄像头相机打交道,于是通过这篇博客记录相机标定相关的知识。首先什么是相机标定?通过相机拍摄到的图像是二维的,而实际上世界的场景是三维的。一个场景通过相机,摄像头转变成二维图像,在这个过程中,把相机看成一个函数,输入是一个三维场景,输出是二维图像。

相机标定是找到一个合适的数学模型,求出这个模型的参数,这样使得这个模型能够近似(逼近)这个三维到二维的过程,从而找到该模型的反函数。

这个近似(逼近)的过程就是相机标定,通过简单的数学模型来表达复杂的成像过程,并且求出成像的反过程。标定之后的相机,可以进行三维场景的重建,即深度的感知,这是计算机视觉的一大分支。同样也可以从另一方面理解,通过三维到二维的过程求得相机的内参、外参以及畸变函数得到数学模型。有了这个数学模型可以对着相机拍摄的图像进行畸变校正,也可以用多个相机拍摄的图像进行三维重建。
相机标定
坐标系
相机的标定涉及到坐标系的转换,那么在标定的过程中涉及那些坐标系呢?或者说坐标系的转换会有哪些坐标系呢。坐标系以此有物体坐标系,世界坐标系,相机坐标系,图像坐标系以及像素坐标系。
- 世界坐标系:点在真实世界中的位置,描述相机位置,单位是m
- 相机坐标系:以相机sensor中心为原点,建立相机坐标系,单位为m
- 图像坐标系:经过小孔成像后得到的二维坐标系,单位为mm
- 像素坐标系:成像点在相机光心(sensor中心点)上像素的行数和列数,原点为图像左上角,不带物理单位
坐标系转换
坐标系的转换大致过程如下:(当然从二维到三维的过程就是其逆过程)
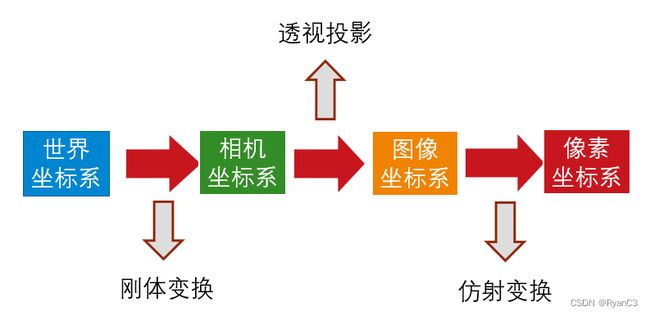
四个坐标系的转化关系如下:
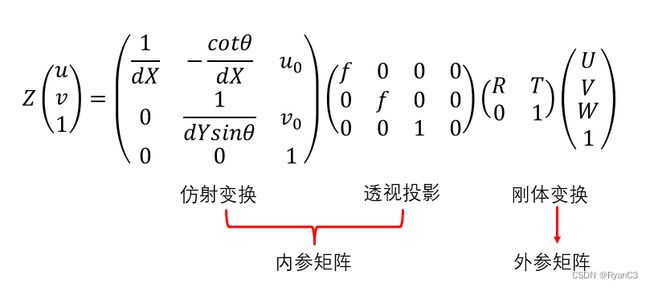
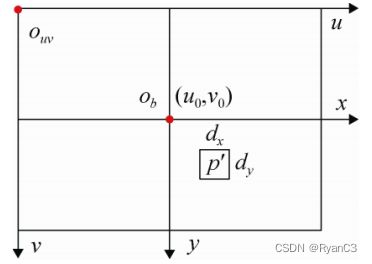
其中, ( U , V , W ) (U, V,W) (U,V,W)为在世界坐标系下一点的物理坐标, ( u , v ) (u, v) (u,v)为该点对应的在像素坐标系下的像素坐标, Z Z Z为尺度因子, f f f为像距, d X dX dX, d Y dY dY分别表示 X X X, Y Y Y方向上的一个像素在相机感光板上的物理长度(即一个像素在感光板上是多少毫米), u 0 u_0 u0, v 0 v_0 v0分别表示相机感光板中心在像素坐标系下的坐标, θ \theta θ表示感光板的横边和纵边之间的角度。
-
世界坐标系–>相机坐标系
在三维世界中有一个点 P w ( X w , Y w , Z w ) P_w(X_w,Y_w, Z_w) Pw(Xw,Yw,Zw)这个点在世界坐标系中。而相机坐标系是以相机位坐标原点,那么相机坐标系不一定等于世界坐标系,除非相机位于世界坐标系的原点上,因此在这个过程需要进行转换。假设相机坐标原点相对于世界坐标原点存在平移向量,记为 t \mathnormal{t} t,相机的旋转角度为 R \mathnormal{R} R,那么可以通过一定的 t \mathnormal{t} t, t \mathnormal{t} t来将世界坐标系转换成相机坐标系。那么我们定义 t \mathnormal{t} t为相机坐标相对于世界坐标系的平移矩阵, R \mathnormal{R} R是相机相对于世界坐标系的旋转矩阵,那么它们的转换关系如下,详情可以参考参考5:
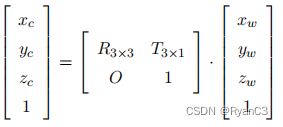
-
相机坐标系->图像坐标系
刚才,在世界坐标系->相机坐标系的转化过程中,通过相机外部的旋转和平移变化,可以和世界坐标系建立一种关联,使两者可以互相转化。那么在相机坐标系->图像坐标系这个转换过程,跟哪些因素有关呢?试想一下,两个不同的相机,即使在所处的位置一样的情况下,拍摄的两张照片,很大概率是不一样的。那么在此次转化过程中,一定离不开相机自身的一些相关的参数。但是跟相机相关的参数有很多,哪些参数能够为这次转化提供帮助呢,需要先了解相机成像的原理。
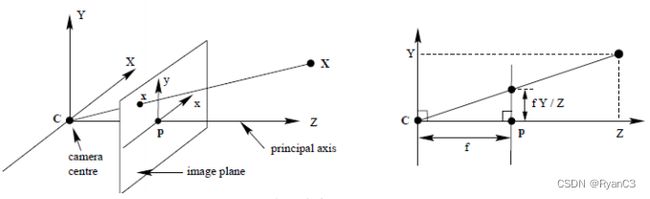
假设相机坐标系上的点为 p ( x c , y c , z c ) p(x_c, y_c, z_c) p(xc,yc,zc),图像坐标系的成像点为 p ′ ( x , y ) p'(x, y) p′(x,y),基于小孔成像原理,假设相机焦距为$ f$ ,成像面是与 XOY 平面平行且距离原点 f 的平面。图1.2的右图为 ZcY 截面。利用相似三角形可以求出:
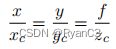
最终结果:

畸变与畸变校正
实际使用中,得到的图像并不是完全按照小孔成像原理进行透视投影,通过透镜后物点在实际的成像平面上的像与理想成像之间存在一点畸变误差。误差主要存在径向畸变和切向畸变两种。径向畸变是由于相机的透镜形状造成的,切向畸变则是整个相机的组装过程中造成的。
沿着透镜的半径方向分布的畸变称为径向畸变。光线在远离透镜中心的地方比靠近中心的地方更加弯曲。径向畸变可以分为,桶形畸变和枕形畸变。如图1.5所示,从左到右分别是,正常无畸变、桶形畸变、枕形畸变。径向畸变是因为,远离透镜中心的光线比靠近透镜中心的光线更加弯曲。廉价的透镜更加严重,高端相机中并不是那么明显。光心的处的畸变为 0,距离越远畸变越大。
一般情况下,图像的径向畸变往往被描述为一个低阶多项式模型。(x, y) 是没有畸变的像素点的位置,(xdistorted, ydistorted) 是径向畸变作用后的点的位置,则二者之间存在以下变换关系:
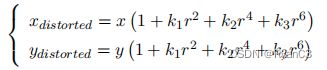
(x, y) 是归一化的图像坐标,即坐标原点已经移动到主点,并且像素坐标除以焦距,r2 = x2 +y2。k1, k2, k3 是径向畸变系数,也属于摄像头的内参。一般使用多项式的前两项,畸变很大的相机比如鱼眼相机会使用第三项。
张氏标定法
张氏标定法利用棋盘格标定板,利用相应的图像检测算法得到每一个角点的像素坐标 ( u , v ) (u, v) (u,v)。 该方法将世界坐标固定于棋盘格上,则棋盘格上任一点的物理坐标 W = 0 W=0 W=0,由于标定板的世界坐标系是人为定义好的,标定板上每一个格子的大小是已知的,可以计算得到每一个角点在世界坐标系下的物理坐标 ( U , V , W = 0 ) (U, V, W=0) (U,V,W=0)。
每一个角点的像素坐标为 ( u , v ) (u, v) (u,v),每一个角点在世界坐标系下的物理坐标为 ( U , V , W = 0 ) (U, V, W=0) (U,V,W=0),来进行相机的标定,获得相机的内外参矩阵、畸变参数。

相机标定的步骤:
- 准备一张棋盘格,棋盘格大小一致,用相机对其进行不同角度的拍摄,得到一组图像
- 对图像中的特征点如标定板角点进行检测,得到标定板角点的像素坐标值,根据已知的棋盘格大小和世界坐标系原点,计算得到标定板角点的物理坐标值
- 求解内参矩阵与外参矩阵
根据物理坐标值和像素坐标值的关系,求出 H H H矩阵,进而构造 v v v矩阵,求解 B B B矩阵,利用 B B B矩阵求解相机内参矩阵 A A A,最后求解每张图片对应的相机外参矩阵 ( R T 0 1 ) \begin{pmatrix} R & T \\ 0 & 1 \end{pmatrix} (R0T1) - 求解畸变参数
利用 u ^ \hat{u} u^, u u u, v ^ \hat{v} v^, v v v构造 D D D矩阵,急死安径向畸变参数 - 利用L-M(Levenberg-Marquardt)算法对上述参数进行优化
具体的推导过程可以参考参考四
参考
- 《相机标定》深入理解原理与实战(一)
- 相机标定(Camera calibration)原理、步骤
- 相机标定究竟在标定什么?
- 相机标定之张正友标定法数学原理详解
- 世界坐标系,相机坐标系,图像坐标系,像素坐标系的转换