自然语言处理系列（一）——RNN基础

注： 本文是总结性文章，叙述较为简洁，不适合初学者

一、为什么要有RNN？

普通的MLP无法处理序列信息（如文本、语音等），这是因为序列是不定长的，而MLP的输入层神经元个数是固定的。

二、RNN的结构

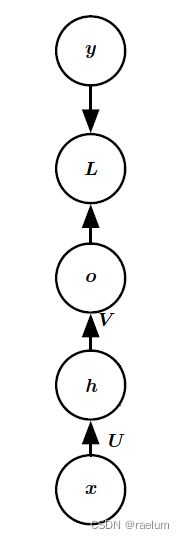
普通MLP的结构（以单隐层为例）：

普通RNN（又称Vanilla RNN，接下来都将使用这一说法）的结构（在单隐层MLP的基础上进行改造）：

即 $t$ 时刻隐藏层接收的输入来自于 $t-1$ 时刻隐藏层的输出和 $t$ 时刻的样例输入。用数学公式表示，就是

$$h^{(t)}=\tanh (W{h}^{(t-1)}+U{x}^{(t)}+b),o^{(t)}=V{h}^{(t)}+c,{\hat{y}}^{(t)}=\text{softmax}(o^{(t)})$$

训练RNN的过程中，实际上就是在学习 $U,V,W,b,c$ 这些参数。

正向传播后，我们需要计算损失，设时间步 $t$ 处求得的损失为 $L^{(t)}=L^{(t)}({\hat{y}}^{(t)},y^{(t)})$，则总的损失为 $L={\sum }_{t=1}^T{L}^{(t)}$。

2.1 BPTT

BPTT（BackPropagation Through Time），通过时间反向传播是RNN训练过程中的一个术语。因为正向传播时是沿着时间流逝的方向进行的，而反向传播则是逆着时间进行的。

为方便后续推导，我们先改进一下符号表述：

$$h^{(t)}=\tanh (W_{hh}{h}^{(t-1)}+W_{xh}{x}^{(t)}+b),o^{(t)}=W_{ho}{h}^{(t)}+c,{\hat{y}}^{(t)}=\text{softmax}(o^{(t)})$$

做一个水平方向的 concatenation：$W=(W_{hh},W_{xh})$，为简便起见，省略偏置 $b$，则有

$$h^{(t)}=\tanh \left(W\left(\begin{array}{c}{h}^{(t-1)}\\ x^{(t)}\end{array}\right)\right)$$

，接下来我们将关注参数 $W$ 的学习。

注意到

$$\frac{\partial h^{(t)}}{\partial h^{(t-1)}}={\tanh }^{\prime }(W_{hh}{h}^{(t-1)}+W_{xh}{x}^{(t)})W_{hh},\frac{\partial L}{\partial W}=\sum _{t=1}^T\frac{\partial L^{(t)}}{\partial W}$$

从而

$$\begin{array}{rl}\frac{\partial L^{(T)}}{\partial W}& =\frac{\partial L^{(T)}}{\partial h^{(T)}}\cdot \frac{\partial h^{(T)}}{\partial h^{(T-1)}}\cdots \frac{\partial h^{(2)}}{\partial h^{(1)}}\cdot \frac{\partial h^{(1)}}{\partial W}\\ & =\frac{\partial L^{(T)}}{\partial h^{(T)}}\cdot \prod _{t=2}^T\frac{\partial h^{(t)}}{\partial h^{(t-1)}}\cdot \frac{\partial h^{(1)}}{\partial W}\\ & =\frac{\partial L^{(T)}}{\partial h^{(T)}}\cdot \left(\prod _{t=2}^T{\tanh }^{\prime }(W_{hh}{h}^{(t-1)}+W_{xh}{x}^{(t)})\right)\cdot W_{hh}^{T-1}\cdot \frac{\partial h^{(1)}}{\partial W}\end{array}$$

因为 ${\tanh }^{\prime }(\cdot )$ 几乎总是小于 $1$ 的，当 $T$ 足够大时将会出现梯度消失现象。

---

假如不采用非线性的激活函数，为简便起见，不妨设激活函数为恒等映射 $f(x)=x$，于是有

$$\frac{\partial L^{(T)}}{\partial W}=\frac{\partial L^{(T)}}{\partial h^{(T)}}\cdot W_{hh}^{T-1}\cdot \frac{\partial h^{(1)}}{\partial W}$$

• 当 $W_{hh}$ 的最大奇异值大于 $1$ 时，会出现梯度爆炸。
• 当 $W_{hh}$ 的最大奇异值小于 $1$ 时，会出现梯度消失。

三、RNN的分类

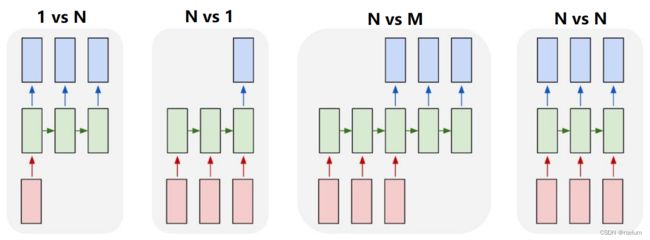
按照输入和输出的结构可以对RNN进行如下分类：

• 1 vs N（vec2seq）：Image Captioning；
• N vs 1（seq2vec）：Sentiment Analysis；
• N vs M（seq2seq）：Machine Translation；
• N vs N（seq2seq）：Video Classification on frame level.

注意 1 vs 1 是传统的MLP。

若按照内部构造进行分类则会得到：

• RNN、Bi-RNN、…
• LSTM、Bi-LSTM、…
• GRU、Bi-GRU、…

四、Vanilla RNN的优缺点

优点：

• 可以处理不定长的序列；
• 计算时会考虑历史信息；
• 权重沿时间方向上是共享的；
• 模型大小不会随着输入大小增加而改变。

缺点：

• 计算效率低；
• 梯度会消失/爆炸（后续将知道，避免梯度爆炸可采用梯度裁剪，避免梯度消失可换用其他的RNN结构，如LSTM）；
• 无法处理长序列（即不具备长记忆性）；
• 无法利用未来的输入（Bi-RNN可解决）。

五、Bidirectional RNN

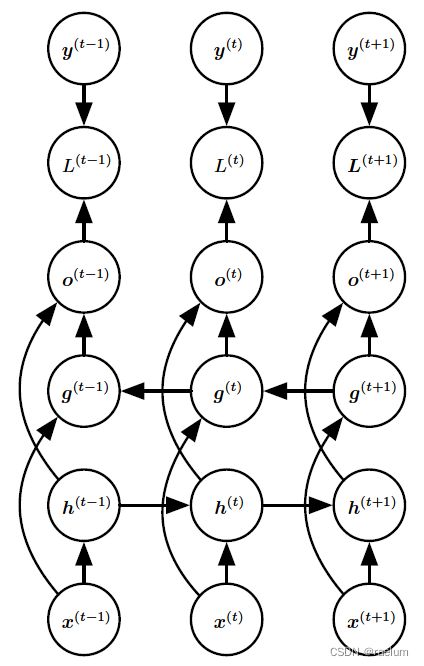
许多时候，我们要输出的 $y^{(t)}$ 可能依赖于整个序列，因此需要使用双向RNN（BRNN）。BRNN结合了时间上从序列起点开始移动的RNN和从序列末尾开始移动的RNN。两个RNN互相独立不共享权重：

相应的计算方式变为：

$$\begin{array}{rl}& h^{(t)}=\tanh (W_1{h}^{(t-1)}+U_1{x}^{(t)}+b_1)\\ & g^{(t)}=\tanh (W_2{h}^{(t-1)}+U_2{x}^{(t)}+b_2)\\ & o^{(t)}=V(h^{(t)};g^{(t)})+c\\ & {\hat{y}}^{(t)}=\text{softmax}(o^{(t)})\end{array}$$

其中 $(h^{(t)};g^{(t)})$ 代表将两个列向量 $h^{(t)}$ 和 $g^{(t)}$ 进行纵向连接。

事实上，若将 $V$ 按列分块，则上述的第三个等式还可写成：

$$o^{(t)}=V(h^{(t)};g^{(t)})+c=(V_1,V_2)\left(\begin{array}{c}{h}^{(t)}\\ g^{(t)}\end{array}\right)+c=V_1{h}^{(t)}+V_2{g}^{(t)}+c$$

训练 BRNN 的过程实际就是在学习 $U_1,U_2,V,W_1,W_2,b_1,b_2,c$ 这些参数。

六、Stacked RNN

堆叠RNN又称多层RNN或深度RNN，即由多个隐藏层组成。以双隐层单向RNN为例，其结构如下：

相应的计算过程如下：

$$\begin{array}{rl}& h^{(t)}=\tanh (W_{hh}{h}^{(t-1)}+W_{xh}{x}^{(t)}+b_h)\\ & z^{(t)}=\tanh (W_{zz}{z}^{(t-1)}+W_{hz}{h}^{(t)}+b_z)\\ & o^{(t)}=W_{zo}{z}^{(t)}+b_o\\ & {\hat{y}}^{(t)}=\text{softmax}(o^{(t)})\end{array}$$