《自然语言处理》教学上机实验报告

《自然语言处理》教学上机实验报告

实验一

基于规则的分词算法

实验目的和要求：
掌握完全切分，正向最长匹配，逆向最长匹配，双向最长匹配，比较三种匹配效率。

实验过程：
1.基于字典、词库匹配的分词方法(基于规则)。这种方法是将待分的句子与一个充分大的词典中的词语进行匹配。常用的有：正向最大匹配，逆向最大匹配，最少切分法。实际应用中，将机械分词作为初分手段，利用语言信息提高切分准确率。优先识别具有明显特征的词，以这些词为断点，将原字符串分为较小字符串再机械匹配，以减少匹配错误率，或将分词与词类标注结合。

2.完全算法指的是，找出一段文本中的所有单词。这并不是标准意义上的分词，有些人将这个过程误称为分词，其实并不准确。
伪代码：

def fully_segment(text, dic):
    word_list = []
    for i in range(len(text)):                  # i从0遍历到text的最后一个字的下标
        for j in range(i + 1, len(text) + 1):   # j遍历[i + 1, len(text)]区间
            word = text[i:j]                    # 取出连续区间[i, j)对应的字符串
            if word in dic:                     # 如果在词典中，则认为是一个词
                word_list.append(word)
    return word_list

在正向最长匹配算法中，算法有可能分出不太令人满意的结果，此时，我们可以尝试逆向最长匹配算法。

3.逆向最长匹配算法和正向匹配方法类似，都是找出一段文本中的所有单词，有所不同的是，逆向最长匹配算法是从逆向来寻找词的。
伪代码：

def backward_segment(text, dic):
    word_list = []
    i = len(text) - 1
    while i >= 0:                              # 扫描位置作为终点
        longest_word = text[i]                  # 扫描位置的单字
        for j in range(0, i):                     # 遍历[0, i]区间作为待查询词语的起点
            word = text[j: i + 1]                 # 取出[j, i]区间作为待查询单词
            if word in dic:
                if len(word) > len(longest_word):   # 越长优先级越高
                    longest_word = word
        word_list.insert(0, longest_word)           # 逆向扫描，因此越先查出的单词在位置上越靠后
        i -= len(longest_word)
    return word_list

4.人们经过尝试上述两种算法，发现有时正向匹配正确，有时逆向匹配正确，但似乎逆向匹配成功的次数更多。为此，人们继续提出新的规则，比如所谓的双向最长匹配。
流程如下：
（1）同时执行正向和逆向最长匹配，若两者的词数不同，则返回词数更少的那一个。
（2）否则，返回两者中单词更少的那一个。当词数也相同时，优先返回逆向最长匹配的结果。
伪代码：

def count_single_char(word_list: list):  # 统计单字成词的个数
    return sum(1 for word in word_list if len(word) == 1)
def bidirectional_segment(text, dic):
    f = forward_segment(text, dic)
    b = backward_segment(text, dic)
    if len(f) < len(b):                                  # 词数更少优先级更高
        return f
    elif len(f) > len(b):
        return b
    else:
        if count_single_char(f) < count_single_char(b):  # 单字更少优先级更高
            return f
        else:
            return b               

实验结果：
原文 正向最长匹配 逆向最长匹配 双向最长匹配
项目的研究 [项目, 的, 研究] [项, 目的, 研究] [项, 目的, 研究]

商品和服务 [商品, 和服, 务] [商品, 和, 服务] [商品, 和, 服务]

研究生命起源 [研究生, 命, 起源] [研究, 生命, 起源] [研究, 生命, 起源]

实验分析：
1.通过本次实验，我掌握了正向最长匹配算法，逆向最长匹配算法，双向最长匹配算法。
2.对于最大长度的选择要谨慎，太长的话影响运行效率，太短可能导致某些词语无法识别。
3.经过实验，发现大部分情况下，逆向最大匹配算法要优于正向最大匹配算法。

实验二

隐马尔可夫模型在分词中的应用（1）

实验目的和要求：
中文分词序列标注的BMES，序列标准初始状态概率向量，状态转移概率矩阵，发射概率矩阵如何求出。

实验过程：
1.了解隐马尔可夫模型
隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别，是在被建模的系统被认为是一个马尔可夫过程与未观测到的（隐藏的）的状态的统计马尔可夫模型。

隐马尔可夫模型是描述两个时序序列联合分布p(x,y)的概率模型
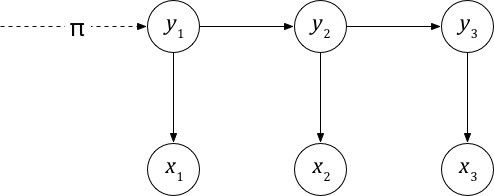
x序列外界可见（外界指的是观测者），称为观测序列（observation sequence），观测x为单词；
y序列外界不可见，称为状态序列（state sequence），状态y为词性，，人们也称状态为隐状态（hidden state），而称观测为显状态（visible state）。

隐马尔可夫模型之所以称为“马尔可夫模型”，是因为它满足马尔可夫假设。

2.初始状态概率向量
系统启动时进入的第一个状态y_1称为初始状态
假设y有N种可能的取值，即y∈{s_1,⋯,s_N}，那么y_1就是一个独立的离散型随机变量，由p(y_1∣π)描述
其中π=(π_1,⋯,π_N )^{T,0≤π_i≤1,∑_(i=1)}N▒π_i =1 是概率分布的参数向量，称为初始状态概率向量。

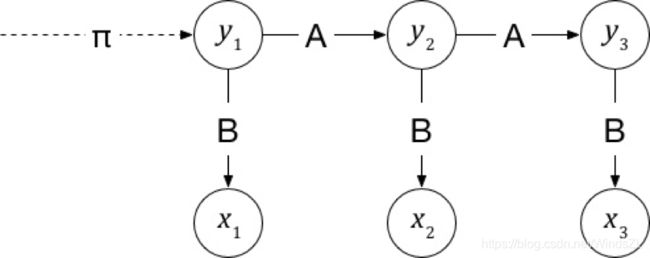
3.状态转移概率矩阵
从状态s_i到状态s_j的概率就构成了一个N×N的方阵，称为状态转移概率矩阵A：
A=[p(y_(t+1)=s_j∣y_t=s_i)]_(N×N)
其中下标i、j分别表示状态的第i、j种取值，比如我们约定1表示标注集中的B，依序类推。

4.发射概率矩阵
给定每种y，x都是一个独立的离散型随机变量，其参数对应一个向量
这些参数向量构成了N×M的矩阵，称为发射概率矩阵B。
B=[p(x_t=o_i∣y_t=s_j)]_(N×M)

5.中文分词序列标注的BMES与隐马尔可夫模型
（1）序列标注与中文分词
{B，M，E，S}法——B（Begin）、E（End）分别表示词语首尾；M（Middle）表示词中；S（Single）表示单字成词。BMES标注完后，分词器将最近两个BE标签对应区间内的所有字符合并为一个词语，S标签对应字符作为单字词语，按顺序输出即完成分词。

（2）序列标注与词性标注**
词性标注任务是一个天然的序列标注问题且不是唯一的，**人们根据需要制定不同的标注集。**如：（）内为标注
参观（动词） 了（助词） 北京（地名） 天安门（地名）

（3）序列标注与命名实体识别
命名实体指的是现实存在的实体，比如人名、地名、机构名。通常简短的人名较好标注，地名、机构名较难识别，这时常常需要在分词和词性标注的中间结果上进行召回。
命名实体识别可以复用BMES标注，沿用中文分词逻辑，只不过标注的对象由字符变为单词。且命名实体识别还需要确定实体所属的类别。如构成地名的单词标注为“B/M/E/S-地名”，对于不构成命名实体的单词，统一标注为O（Outside）。

样例如下：
参观 了 北京 天安门
（O） （O）（B—地名）（E—地名）
首先对中文分词进行标注，根据语料计算三个概率矩阵
当获得了分好词的语料之后，三个概率可以通过如下方式获得：

(1)初始状态概率P(y1)
统计每个句子开头，序列标记分别为B，S的个数，最后除以总句子的个数，即得到了初始概率矩阵。

(2) 状态转移概率P(yi|yi-1)
根据语料，统计不同序列状态之间转化的个数，例如count(yi=”E”|yi-1=”M”)为语料中i-1时刻标为“M”时，i时刻标记为“E”出现的次数。得到一个4*4的矩阵，再将矩阵的每个元素除以语料中该标记字的个数，得到状态转移概率矩阵。

(3) 输出观测概率P(xi|yi)
根据语料，统计由某个隐藏状态输出为某个观测状态的个数，例如count(xi=”深”|yi=”B”)为i时刻标记为“B”时，i时刻观测到字为“深”的次数。得到一个4*N的矩阵，再将矩阵的每个元素除以语料中该标记的个数，得到输出观测概率矩阵。
接下来，便可以使用维比特算法，获得一个句子的最大概率分词标记序列。具体过程不再赘述。

python代码展示如下：

# -*- coding:utf-8 -*-
import numpy as np
from pyhanlp import *
from jpype import JArray, JFloat, JInt

to_str = JClass('java.util.Arrays').toString

states = ('Healthy', 'Fever')
start_probability = {'Healthy': 0.6, 'Fever': 0.4}
transition_probability = {
    'Healthy': {'Healthy': 0.7, 'Fever': 0.3},
    'Fever': {'Healthy': 0.4, 'Fever': 0.6},
}
emission_probability = {
    'Healthy': {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
    'Fever': {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6},
}
observations = ('normal', 'cold', 'dizzy')

def generate_index_map(lables):
    index_label = {}
    label_index = {}
    i = 0
    for l in lables:
        index_label[i] = l
        label_index[l] = i
        i += 1
    return label_index, index_label

states_label_index, states_index_label = generate_index_map(states)
observations_label_index, observations_index_label = generate_index_map(observations)

def convert_observations_to_index(observations, label_index):
    list = []
    for o in observations:
        list.append(label_index[o])
    return list

def convert_map_to_vector(map, label_index):
    v = np.empty(len(map), dtype=float)
    for e in map:
        v[label_index[e]] = map[e]
    return JArray(JFloat, v.ndim)(v.tolist())  # 将numpy数组转为Java数组

def convert_map_to_matrix(map, label_index1, label_index2):
    m = np.empty((len(label_index1), len(label_index2)), dtype=float)
    for line in map:
        for col in map[line]:
            m[label_index1[line]][label_index2[col]] = map[line][col]
    return JArray(JFloat, m.ndim)(m.tolist())

A = convert_map_to_matrix(transition_probability, states_label_index, states_label_index)
B = convert_map_to_matrix(emission_probability, states_label_index, observations_label_index)
observations_index = convert_observations_to_index(observations, observations_label_index)
pi = convert_map_to_vector(start_probability, states_label_index)

FirstOrderHiddenMarkovModel = JClass('com.hankcs.hanlp.model.hmm.FirstOrderHiddenMarkovModel')
given_model = FirstOrderHiddenMarkovModel(pi, A, B)

for O, S in given_model.generate(3, 5, 2):
    print(" ".join((observations_index_label[o] + '/' + states_index_label[s]) for o, s in zip(O, S)))

trained_model = FirstOrderHiddenMarkovModel()
trained_model.train(given_model.generate(3, 10, 100000))
assert trained_model.similar(given_model)
trained_model.unLog()  # 将对数形式的概率还原回来

实验结果：

实验分析：
1.序列标注问题包括自然语言处理中的分词，词性标注，命名实体识别，关键词抽取，词义角色标注等等。我们只要在做序列标注时给定特定的标签集合，就可以进行序列标注。
2.序列标注问题是NLP中最常见的问题，因为绝大多数NLP问题都可以转化为序列标注问题，虽然很多NLP任务看上去大不相同，但是如果转化为序列标注问题后其实面临的都是同一个问题。

实验三：

隐马尔可夫模型在分词中的应用（2）

实验目的和要求：
内容：已知语料库中有且仅有如下3个句子：
商品 和 服务
商品 和服 物美价廉
服务 和 货币
应用隐马尔可夫模型和维特比算法给出‘商品和货币’这句话的分词结果。

实验过程：
1.维比特算法
维特比算法是一种动态规划方法。动态规划的基础是贝尔曼最优性原理（Bellman’s Principle of Optimality）：多级决策过程的最优策略（最优序列）有这样的性质：不论初始状态和初始决策如何，其余的决策对于初始决策所形成的状态来说，必定也是一个最优策略。维特比算法利用以下的方法求解最优序列：从起始时刻t=1开始，递推地找出在时刻t的状态为Si的各个可能的状态序列中的最大概率，一直求解到时刻t=T的状态为Si的最大概率，并得到时刻T的状态Sj；然后向前回溯求得其他时刻的状态。

2.根据语料库，因为样本空间大小为3，所以仅有的3个句子平分了所有的概率，即它们的概率都是1/3，其他所有句子的概率均为0。所以语言模型p(w)如下所示：
p(商品 和 服务) = 1/3

p(商品 和服 物美价廉) = 1/3

p(服务 和 货币) = 1/3

这个语言模型只能用来判断已有的这3个句子，而其他的句子因为概率都是0而无法判断。
一个方式就是增大样本数量，但是句子总数无穷无尽，无法枚举，即使是大型语料库，也只能“枚举”几百万个句子。因此，无论我们使用多达的语料库，绝大部分的句子还是在语料库之外，即它们的概率仍然为0，这个现象被称为数据稀疏。

由此，我们考虑到句子数虽然是无限的，但是句子中包含的词却是有限的。于是我们尝试从构成句子的角度去建模句子，即通过已经说出口的所有的词语，来预测下一个词语。

在预测的过程中，我们将句子的开头和结尾当做两个特殊的单词，分别记作BOS(Begin of Sentence)和EOS(End of Sentence)。

在当前算法下，句子“商品 和 服务“的概率的计算结果如下：
p(商品|BOS) = 2/3

p(和|BOS 商品) = 1/2

p(服务|BOS 商品 和) = 1/1

p(EOS|BOS 商品 和 服务) = 1/1

p(商品 和 服务) = p(商品|BOS) + p(和|BOS 商品) + p(服务|BOS 商品 和) + p(EOS|BOS 商品 和 服务) = 2/3 * 1/2 * 1/1 * 1/1 = 1/3

此时语言模型p(w)如下所示：

p(商品 和 服务) = 1/3

p(商品 和服 物美价廉) = 1/3

p(服务 和 货币) = 1/3

这样仍然只能识别语料库中的文本，语料库外的文本的概率仍然为0，存在数据稀疏的问题。

马尔可夫链
为了解决这个问题，我么引入马尔科夫假设：给定时间线上有一串事件顺序发生，假设每个事件的发生概率只取决于前一个事件，那么这串事件构成的因果链就被称为马尔可夫链。

基于此假设，每次计算只涉及两个单词的二元接续，此时的语言模型称为二元语法模型。

在当前算法下，句子“商品 和 服务“的概率的计算结果如下：
p(商品|BOS) = 2/3

p(和|商品) = 1/2

p(服务|和) = 1/2

p(EOS|服务) = 1/2

p(商品 和 服务) = p(商品|BOS) + p(和|BOS 商品) + p(服务|BOS 商品 和) + p(EOS|BOS 商品 和 服务) = 2/3 * 1/2 * 1/2 * 1/2 = 1/12

此时语言模型p(w)如下所示：

p(商品 和 服务) = 1/12 = 2/24

p(商品 和服 物美价廉) = 1/3 = 8/24

p(服务 和 货币) = 1/8 = 3/24

p(商品 和 货币) = 1/6 = 4/24

p(服务) = 1/6 = 4/24

p(服务 和 服务) = 1/24

p(商品 和 服务 和 …) = 1/24

p(服务 和 服务 和 …) = 1/24

可见，当前的语言模型不但可以识别语料库中的文本，也可以识别一部分的语料库外的文本了，缓解了一部分数据稀疏的问题。

n元语法
利用类似的思路，我们得到n元语法的定义：每个单词的概率仅取决于该单词之前的n-1个单词。通常而言，实际工程中不会使用n≥4的算法。

另外，深度学习也剔除了一种递归神经网络语言模型(RNN Language Model)，理论上可以记忆无限个单词，可以看作“无穷元语法”。

实验结果：

商品和货币的概率为16/117649

实验分析：
1.训练指的是统计二元语法频次以及一元语法频次，有了频次，通过极大似然估计以及平滑策略，我们就可以估计任意句子的概率分布，即得到了语言模型。
2.HMM不只用于中文分词，如果把 S 换成句子，O 换成语音信号，就变成了语音识别问题，如果把 S 换成中文，O 换成英文，就变成了翻译问题，如果把 S 换成文字，O 换成图像，就变成了文字识别问题，此外还有词性标注等等问题。
对于上述每种问题，只要知道了五元组中的三个参数矩阵，就可以应用 Viterbi 算法得到结果。

实验四

基于K-means的文本聚类方法

实验目的和要求：
记录有某音乐网站6位用户点播的歌曲流派，给定用户名称和九种音乐类型的播放数量，通过K-means将6位用户分成3簇（把播放数量当成数组或者向量进行簇质心的迭代运算）。

实验过程：
一、了解聚类：
1.聚类的过程
（1）特征选择：就像其他分类任务一样，特征往往是一切活动的基础，如何选取特征来尽可能的表达需要分类的信息是一个重要问题。表达性强的特征将很影响聚类效果。这点在以后的实验中我会展示。
（2）近邻测度：当选定了实例向量的特征表达后，如何判断两个实例向量相似呢？这个问题是非常关键的一个问题，在聚类过程中也有着决定性的意义，因为聚类本质在区分相似与不相似，而近邻测度就是对这种相似性的一种定义。
（3）聚类准则：定义了相似性还不够，结合近邻测度，如何判断相似才是关键。直观理解聚类准则这个概念就是何时聚类，何时不聚类的聚类条件。当我们使用聚类算法进行计算时，如何聚类是算法关心的，而聚与否需要一个标准，聚类准则就是这个标准。
（4）聚类算法：这个东西不用细说了吧，整个学习的重中之重，核心的东西这里不讲，以后会细说，简单开个头——利用近邻测度和聚类准则开始聚类的过程。
（5）结果验证(validation of the results)：其实对于PR的作者提出这个过程也放到聚类任务流程中，我觉得有点冗余，因为对于验证算法的正确性这事应该放到算法层面吧，可以把4）和5）结合至一层。因为算法正确和有穷的验证本身就是算法的特性。

2.聚类的准则
聚类准则就是一个分类标准，对于示例中这样一个数据集合，如何聚类呢。当然聚类的可能情况有很多。比如，如果我们按照年级是否为大于1来分类，那么数据集X分为两类：{张三}，{李四，张飞，赵云}；如果按照班级不同来分，分为两类：{张三，李四}，{张飞，赵云}；如果按照成绩是否及格来分（假设及格为60分），分两类：{张三，李四，赵云}，{张飞}。当然聚类准则的设计往往是复杂的，就看你想怎么划分了。按照对分类思想的几何理解，数据集相当于样本空间，数据实例的特征数（本例共有4个特征[姓名，年级，班级，数学成绩]）相当于空间维度，而实例向量对应到空间中的一个点。那么聚类准则就应该是那些神奇的超平面（对应有数学函数表达式，我个人认为这些函数就等同于聚类准则），这些超平面将数据“完美的”分离开了。

3.聚类特征类型
聚类时用到的特征如何区分呢，有什么类型要求？聚类的特征按照域划分，可以分为连续的特征和离散特征。其中连续特征对应的定义域是数据空间R的连续子空间，而离散特征对应的是离散子集，另外如果离散特征只包含两个特征值，那么这个离散特征又叫二值特征。 根据特征取值的相对意义又可以将特征分为以下四种：标量的(Nominal)，顺序的(Ordinal)，区间尺度的(Interval-scaled)以及比率尺度的(Ratio-scaled)。其中，标量特征用于编码一类特征的可能状态，比如人的性别，编码为男和女；天气状况编码为阴、晴和雨等。顺序特征同标量特征类似，同样是一系列状态的编码，只是对这些编码稍加约束，即编码顺序是有意义的，比如对一道菜，它的特征有{很难吃，难吃，一般，好吃，美味}几个值来定义状态，但是这些状态是有顺序意义的。这类特征我认为就是标量特征的一个特定子集，或者是一个加约束的标量特征。区间尺度特征表示该特征数值之间的区间有意义而数值的比率无意义，经典例子就是温度，A地的温度（20℃）比B地（15℃）高5度，这里的区间差值是有意义的，但你不能说A地比B地热1/3，这是无意义的。比率特征与此相反，其比率是有意义的，经典例子是重量，C重100g，D重50g，那么C比D重2倍，这是有意义的。（当然说C比D重50g也是可以的，因此可以认为区间尺度是比率尺度的一个真子集）。

4.聚类算法的分类
（1）划分方法
划分方法就是根据用户输入值k把给定对象分成k组（满足2个条件：1. 每个组至少包含一个对象。2. 每个对象必须且只属于一个组），每组都是一个聚类，然后利用循环再定位技术变换聚类里面的对象，直到客观划分标准（常成为相似函数，如距离）最优为止。典型代表：k-means, k-medoids 层次的方法。

层次的方法对给定的对象集合进行层次分解。分为2类：凝聚的和分裂的。凝聚的方法也叫自底向上的方法，即一开始将每个对象作为一个单独的簇，然后根据一定标准进行合并，直到所有对象合并为一个簇或达到终止条件为止。分裂的方法也叫自顶向下的方法，即一开始将所有对象放到一个簇中，然后进行分裂，直到所有对象都成为单独的一个簇或达到终止条件为止。典型代表：CURE,BIRCH
（2）基于密度的方法
基于密度的方法即不断增长所获得的聚类直到邻近（对象）密度超过一定的阀值（如一个聚类中的对象数或一个给定半径内必须包含至少的对象数）为止。典型代表：DBSCAN，OPTICS。
（3）基于网格的方法
基于网格的方法即将对象空间划分为有限数目的单元以形成网格结构。所有聚类操作都在这一网格结构上进行。典型代表：STING。
（4）基于模型的方法
基于模型的方法即为每个聚类假设一个模型，然后按照模型去发现符合的对像。这样的方法经常基于这样的假设：数据是根据潜在的概率分布生成的。主要有2类：统计学方法和神经网络方法。典型代表：COBWEB，SOMs

5.什么是k-means
K-means算法是很典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

k个初始类聚类中心点的选取对聚类结果具有较大的影响，因为在该算法第一步中是随机的选取任意k个对象作为初始聚类的中心，初始地代表一个簇。该算法在每次迭代中对数据集中剩余的每个对象，根据其与各个簇中心的距离将每个对象重新赋给最近的簇。当考察完所有数据对象后，一次迭代运算完成，新的聚类中心被计算出来。如果在一次迭代前后，J的值没有发生变化，说明算法已经收敛。

算法过程
1）从N个文档随机选取K个文档作为质心
　2）对剩余的每个文档测量其到每个质心的距离，并把它归到最近的质心的类
　3）重新计算已经得到的各个类的质心
　4）迭代2～3步直至新的质心与原质心相等或小于指定阀值，算法结束
说明如下：首先从n个数据对象任意选择 k 个对象作为初始聚类中心；而对于所剩下其它对象，则根据它们与这些聚类中心的相似度（距离），分别将它们分配给与其最相似的（聚类中心所代表的）聚类；然 后再计算每个所获新聚类的聚类中心（该聚类中所有对象的均值）；不断重复这一过程直到标准测度函数开始收敛为止。一般都采用均方差作为标准测度函数. k个聚类具有以下特点：各聚类本身尽可能的紧凑，而各聚类之间尽可能的分开。
　　具体如下：
　　 输入：k, data[n];
　　（1） 选择k个初始中心点，例如c[0]=data[0],…c[k-1]=data[k-1]；
　　（2） 对于data[0]….data[n]，分别与c[0]…c[k-1]比较，假定与c[i]差值最少，就标记为i；
　　（3） 对于所有标记为i点，重新计算c[i]={ 所有标记为i的data[j]之和}/标记为i的个数；
　　（4） 重复(2)(3)，直到所有c[i]值的变化小于给定阈值。

6.什么是TD－IDF
TF-IDF（term frequency–inverse document frequency）是一种用于资讯检索与资讯探勘的常用加权技术。TF-IDF是一种统计方法，用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。

TF-IDF算法是建立在这样一个假设之上的：对区别文档最有意义的词语应该是那些在文档中出现频率高，而在整个文档集合的其他文档中出现频率少的词语，所以如果特征空间坐标系取TF词频作为测度，就可以体现同类文本的特点。另外考虑到单词区别不同类别的能力，TFIDF法认为一个单词出现的文本频数越小，它区别不同类别文本的能力就越大。因此引入了逆文本频度IDF的概念，以TF和IDF的乘积作为特征空间坐标系的取值测度，并用它完成对权值TF的调整，调整权值的目的在于突出重要单词，抑制次要单词。

7.k-means 的文本聚类
前面介绍了TD－IDF我们可以通过用TD－IDF衡量每个单词在文件中的重要程度。如果多个文件，它们的文件中的各个单词的重要程度相似，我就可以说这些文件是相似的。如何评价这些文件的相似度呢？一种很自然的想法是用两者的欧几里得距离来作为相异度，欧几里得距离的定义如下：

其意义就是两个元素在欧氏空间中的集合距离，因为其直观易懂且可解释性强，被广泛用于标识两个标量元素的相异度。我们可以将X，Y分别理解为两篇文本文件，xi,y是每个文件单词的TD－IDF值。这样就可以算出两文件的相似度了。这样我们可以将文件聚类的问题转化为一般性的聚类过程，样本空间中的两点的距离可以欧式距离描述。除欧氏距离外，常用作度量标量相异度的还有曼哈顿距离和闵可夫斯基距离。

整个文本聚类过程可以先后分为两步：
1、计算文本集合各个文档中TD－IDF值，2，根据计算的结果，对文件集合用k-means聚类方法进行迭代聚类。
TD-IDF的计算
（1）假设文档集合T ＝｛n|tn, n>1｝。
（2）对文档进行分词或Tokennize处理，去掉停用词。
（3）计算各个词出现的次数freq(wi),则TF(i) = freq(wi)/sum( freq(w1…n)) ,有时候sum( freq(w1…n))可以用max( freq(w1…n))，做归一处理。
（4）统计文件集合中有词wj出现的文件个数doc_freq(wj).则IDF＝ 1/log(doc_freq(wj);
（5）根据上面的计算我们可以算出文件i，单词wj的TD－IDF权值W[i][j]= TD(j)*IDF(j)。其中i为文件集合T中的一个文件，而j是文件集合T中的一个单词。
通过对文件集合T的计算我们可以得到一个二维数组(矩阵)W[i][j].

K-means聚类的迭代过程
（1）随机选取k个文件生成k个聚类cluster,k个文件分别对应这k个聚类的聚类中心Mean(cluster) = k ;对应的操作为从W[i][j]中0～i的范围内选k行（每一行代表一个样本），分别生成k个聚类，并使得聚类的中心mean为该行。
（2）对W[i][j]的每一行，分别计算它们与k个聚类中心的距离（通过欧氏距离）distance(i,k)。
（3）对W[i][j]的每一行，分别计算它们最近的一个聚类中心的n(i) = ki。
（4）判断W[i][j]的每一行所代表的样本是否属于聚类，若所有样本最近的n(i)聚类就是它们的目前所属的聚类则结束迭代，否则进行下一步。
（5）根据n(i) ，将样本i加入到聚类k中，重新计算计算每个聚类中心（去聚类中各个样本的平均值），调到第2步。

# k-均值支持函数
def loadDataSet(fileName):
    # 用于读取文本数据
	dataMat = []
	fr = open(fileName)
	for line in fr.readlines():
		curLine = line.strip().split('\t')   # 清除文本格式 转换成数组
		fltLine = map(float, curLine)   # map知识
        # map(function, data) 将函数function作用于数据data (类似用法：reduce) 
		dataMat.append(fltLine)     # 收集数据
	return dataMat
 
def  distEclud(vecA, vecB):
    # 用于计算两个向量之间的欧氏距离 
	return sqrt(sum(power(vecA - vecB, 2 )))
 
def randCent(dataSet, k):
    # 构建类（簇）质心 
    # n 获取dataSet的列数 也可以写作 dataSet.shape[1]
	n = shape(dataSet)[1]
    # 然后构建一个（k,n）初始0矩阵 用于后续保存质心
	centroids = mat(zeros((k, n)))
    # 开始初始类质心 需要注意的是 要保证初始质心是在所允许的范围内 
	for j in range(n):
		minJ = min(dataSet[:,j])   # 找到数据集所有列的最小值
		rangeJ = float(max(dataSet[:,j]) - minJ)  # 列最大值-列最小值 得出取值范围
        # 需要注意的是 这是从第一列开始 对每列进行确定取值范围 然后进行在该取值范围内随机取值
		centroids[:, j] = minJ + rangeJ * random.rand(k, 1)  
        # 以最小值为下限 随机在（0,1）内进行取值 通过取值范围rangeJ和最小值minJ进行
        # 随机点都落在 数据边界之内
	return centroids

实验结果：

李四和钱二同属一个簇，这两人都喜欢爵士和舞曲，王五和赵一都喜欢流行和摇滚音乐，张三和马六都喜欢古典音乐

实验分析：
k均值聚类算法（k-means clustering algorithm）是一种迭代求解的聚类分析算法，其步骤是，预将数据分为K组，则随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。