SIFT图像匹配原理及python实现(源码实现及基于opencv实现)
写在前面
黄宁然,看过你看过的算法,数学不好是硬伤。
问题来源:
An***** xue100: https://bbs.csdn.net/topics/*********?spm=1001.2014.3001.**77
(1)相机置于地面,离天花板的高度始终不变。在某位置拍一张图,然后相机移动一定距离、旋转一定角度后再拍一张图。这2张图上的特征点,在梯度值和梯度方向上是否一致呢?
(2)opencv不提供单独点的特征,除非自己动手实现。
1.参考文献镇楼
[0]David G.Lowe,distinctive image features from scale invariant keypoints.pdf
[1]郑昊,基于改进SIFT算法的图像匹配算法研究
[2]许昕健,SIFT图像匹配算法的FPGA加速实现
[3] Derle3er,python实现SIFT算法,附详细公式推导和代码
(https://blog.csdn.net/sakurakawa/article/details/120833167?spm=1001.2014.3001.5502)
[4] Brook_icv,SIFT特征详解(https://www.cnblogs.com/wangguchangqing/p/4853263.html)
[5]zddhub,SIFT算法详解(https://blog.csdn.net/zddblog/article/details/7521424)
[6] rmislam,SIFT源码,(https://github.com/rmislam/PythonSIFT)
[7]梁爽,基于SIFT算子的影像匹配方法研究
[8]邱晓冬,基于FPGA的SIFT图像匹配系统实现与优化
[9]冯邵封,opencv中match与KnnMatch返回值解释(https://blog.csdn.net/weixin_44072651/article/details/89262277 )
2. SIFT算法概述
SIFT全称为Scale Invariant Feature Transform,译为尺度不变特征变换。主要是用来求取图像的特征。其具有尺度不变性、旋转不变性、亮度不变性[1]。
一般,找图像的特征,即是找图像中的特征点,SIFT算法也是如此,其主要任务就是找到图像中的特征点。而特征点,一般就是找图像在某些方面的极值点,例如像素值上的极值点。找极值点,一般会比较差值,例如通过差值,找图像边缘。
好的特征点寻找算法,应该不随图像的尺度变化(例如图像放大、缩小)、旋转变化、亮度变化而变。例如,经算法处理,某图像位置,在图像1:1放大情况下,为极值点,在图像1:0.5放大情况下,也是极值点,那么该极值点即比较可信。
总体来说,SIFT算法,包括以下几个步骤:构造尺度空间、寻找极值点、计算极值点方向、生成极值点的描述[2]。
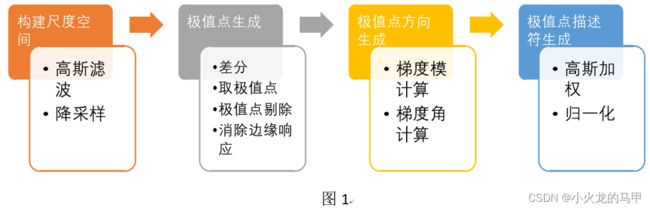
(1)构造尺度空间,即是求取图像在不同尺度下变换图像(例如1:1,1:0.5等),结合高斯滤波、降采样方式获得;
(2)寻找极值点,即是综合各尺度下的图像(差分图像),寻找极值位置,即不仅仅是在某张图像上找极值点,而是在多张不同尺度的图像上寻找极值点,目的是提取多个尺度下的共有特征。因为,在多个尺度中同时存在的特征,便具备了不同程度的尺度不变性,如果某特征横跨的尺度越多,那么其不变性就越好[2]。
(3)寻找极值点,仅仅是获取到了位置、尺度信息,为满足旋转不变性,还需涵盖极值点的方向信息,例如计算梯度方向,获取极值点方向;计算梯度模,作为极值点的幅值强度;
(4)生成极值点描述时,一方面,将极值点信息的幅度信息归一化,便可保证亮度不变性,类似的,再将极值点方向信息“归一化”(例如将图像旋转一定角度,将极值点方向归零),便可保证旋转不变性(个人理解)。
下面,从这几个方面开始具体分析。
3.构造尺度空间
3.1 简述
尺度空间构造,主要是对图像进行降采样、高斯滤波。直接上图[2].
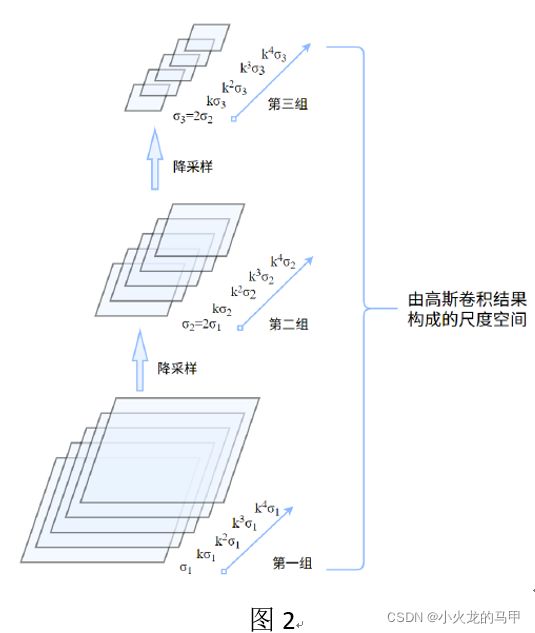
构建尺度空间,实际上在求取图像高斯金字塔。如图2,假设第一组为原始图像尺寸大小,第二组为第一组的1/2尺寸降采样,第3组继续1/2降采样。如果仅仅进行降采样操作,可能略显粗糙。这里,再引入高斯尺度空间,即对每一组输入图像,使用不同标准差σ对图像进行高斯滤波。高斯滤波的重要参数是标准差σ,代表尺度因子。σ越大,模糊越厉害,看的越全局概貌。
结合图2,首先看第一组,分别使用 σ 1 、 K σ 1 、 K 2 σ 1 … σ_1 、Kσ_1 、K^2 σ_1… σ1、Kσ1、K2σ1…一系列标准差对输入图像进行高斯滤波。这一系列标准差(尺度)便构成该组内的不同尺度s,称为层,而这一组又称为一个octave,每个组内的各尺度下的图像,尺寸相同。第二组图像,首先由第一组图像进行降采样,然后同样使用一系列标准差对图像进行高斯滤波处理,构成第二组图像的尺度空间。
为保证连续性,第二组的初始标准差为第一组初始标准差的2倍。
假设,每一组共进行S层尺度滤波,则取每组相邻层之间的尺度因子系数:
![]()
对于第一组,各s层的标准差为:
![]()
对于第o组,第s层,标准差为:
![]()
这里 σ 0 σ_0 σ0为初始标准差(初始尺度因子)。
对于第一组,当s=S+1时, σ s = σ 0 ∗ 2 σ_s=σ_0*2 σs=σ0∗2,正好为下一组的初始标准差。
所以,将s=S+1层的高斯滤波结果图像,进行1/2的降采样,作为第二组的输入图像。
注意:
(1)高斯滤波的性质,对图像依次进行 σ 1 、 σ 2 σ_1 、σ_2 σ1、σ2的两次高斯滤波,等同于对图像进行一次 σ 3 σ_3 σ3高斯滤波,并且有如下约束条件: σ 3 2 = σ 1 2 + σ 2 2 σ_3^2= σ_1^2+σ_2^2 σ32=σ12+σ22
所以,对于每一组,下一层的高斯滤波结果可在上一次的高斯滤波结果上进行,只要求出中间标准差 σ 2 σ_2 σ2即可。
(2)对于每一组,在求取该组图像的高斯滤波时,根据(式3),可知σ是与octave有关的。但在rmislam[6]的代码中,该组的σ的取值仅仅与层s有关。为什么?是否是因为:对于每一组,该组的输入图像已经在上组的基础上进行了1/2降采样,涵盖了 2 o 2^o 2o的信息,即(式3)指的是相对于原始输入图像的尺度因子,而不是相对于该组octave下的尺度因子。不知这样理解是否正确?
(3)对于输入图片,若为相机拍照所得,则相机一般已经进行了σ=0.5的模糊,这在后续计算中,需要考虑折算。
(4)关于构造尺度空间的参数选取。
据文献[7],D.G.Lowe建议σ=1.6,S=3。高斯金子塔组数o的确定:
![]()
M、N为图像的宽和高。
另外,后续求差分层的极值点,是同时比较该差分层与上层、下层的像素值,为得到S层个结果,需要S+2个差分层,需要S+2+1个高斯层。具体见下文描述。所以,组内的倒数第3层(s=S+1)的尺度正好为下一组的初始尺度。
3.2 python代码
#coding=utf8
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import math
import cv2
import os,sys
import scipy.ndimage
import time
import scipy
from numpy.linalg import det, lstsq, norm
from functools import cmp_to_key
(1)定义CSift类,用于参数传递
###################################################### 1. 定义SIFT类 ####################################################
class CSift:
def __init__(self,num_octave,num_scale,sigma):
self.sigma = sigma #初始尺度因子
self.num_scale = num_scale #层数
self.num_octave = 3 #组数,后续重新计算
self.contrast_t = 0.04#弱响应阈值
self.eigenvalue_r = 10#hessian矩阵特征值的比值阈值
self.scale_factor = 1.5#求取方位信息时的尺度系数
self.radius_factor = 3#3被采样率
self.num_bins = 36 #计算极值点方向时的方位个数
self.peak_ratio = 0.8 #求取方位信息时,辅方向的幅度系数
(2)预处理图片
###################################################### 2. 构建尺度空间 ####################################################
def pre_treat_img(img_src,sigma,sigma_camera=0.5):
sigma_mid = np.sqrt(sigma**2 - (2*sigma_camera)**2)#因为接下来会将图像尺寸放大2倍处理,所以sigma_camera值翻倍
img = img_src.copy()
img = cv2.resize(img,(img.shape[1]*2,img.shape[0]*2),interpolation=cv2.INTER_LINEAR)#注意dstSize的格式,行、列对应高、宽
img = cv2.GaussianBlur(img,(0,0),sigmaX=sigma_mid,sigmaY=sigma_mid)
return img
可见,此处返回的img为σ=sigma=1.6的高斯滤波结果
(3)计算高斯金字塔组数
def get_numOfOctave(img):
num = round (np.log(min(img.shape[0],img.shape[1]))/np.log(2) )-1
return num
(4)构建高斯金子塔
def construct_gaussian_pyramid(img_src,sift:CSift):
pyr=[]
img_base = img_src.copy()
for i in range(sift.num_octave):#共计构建octave组
octave = construct_octave(img_base,sift.num_scale,sift.sigma) #构建每一个octave组
pyr.append(octave)
img_base = octave[-3]#倒数第三层的尺度与下一组的初始尺度相同,对该层进行降采样,作为下一组的图像输入
img_base = cv2.resize(img_base,(int(img_base.shape[1]/2),int(img_base.shape[0]/2)),interpolation=cv2.INTER_NEAREST)
return pyr
构建每一个组
def construct_octave(img_src,s,sigma):
octave = []
octave.append(img_src) #输入的图像已经进行过GaussianBlur了
k = 2**(1/s)
for i in range(1,s+3):#为得到S层个极值结果,需要构建S+3个高斯层
img = octave[-1].copy()
cur_sigma = k**i*sigma
pre_sigma = k**(i-1)*sigma
mid_sigma = np.sqrt(cur_sigma**2 - pre_sigma**2)
cur_img = cv2.GaussianBlur(img,(0,0),sigmaX=mid_sigma,sigmaY=mid_sigma)
octave.append(cur_img)
return octave
4.找极值点(关键点)位置
4.1 高斯差分层DoG[2]
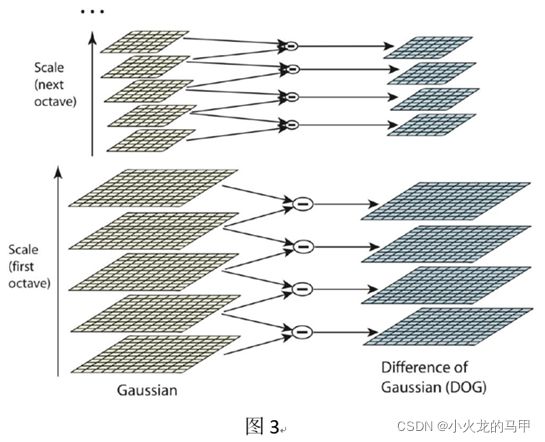
找极值点,一般在差分结果上寻找,关注图像局部的突变部分,如点、线、边缘等。SIFT算法从图像的高斯-拉普拉斯LoG结果中检测极值点位置,但为减少计算量,使用DoG代替,即对于图2中的每一组高斯层,做差分处理,得到DoG,如图3。
4.2 寻找初步极值点
对于图3中的每一组(octave)下的每一层(s)DOG,寻找极值点,如图4所示。对于图4中的x位置,除了比较本层的3*3邻域外,还比较上层、下层邻域,即共计比较26个像素点。所以,符合条件的极值点,其位置应该包括组信息octave、层信息scale、XY信息。
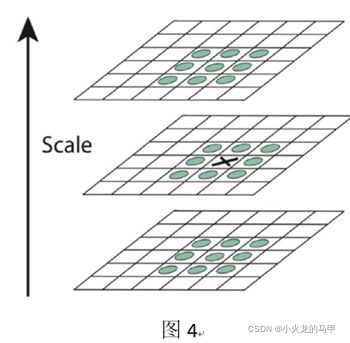
所以,为得到S层个极值点结果,需要构建S+2个DoG层,需要构建S+3个高斯层。
注意:
在DoG上找初步极值点时,极值点需要大于一定阈值(contrast threshold)才能认可。据文献[8]描述,“对于极值点的第一步筛选是剔除那些DoG图像过小的点,这些点由于响应过小,易受到噪声干扰而变得不稳定”,假设图像灰度值在[0,1]之间,文献[8]取阈值为0.03。而Derle3er [3]取阈值为0.04,并经过下面公式计算得到最终阈值(原始图像像素值范围为0~255):
threshold = floor(0.5 * contrast_threshold / num_intervals * 255)
其中,num_intervals为分解尺度S,这在文献[1]中式(2-11)有提及,为何乘以0.5,不明。
此外,在接下来的插值获取精确定位之后,还会再次进行弱灰度值的剔除。
4.3 插值获得精确极值点位置
初步极值点寻找到后,需插值得到精确位置。因是在组内寻找极值点,所以插值需要用到层σ、及x、y信息。将像素值看成是这3个变量的函数f(x,y, σ),使用泰勒展开,将f在(x0,y0, σ0)展开到2次,如下所示[3]。
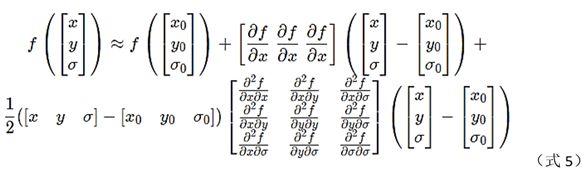
各阶偏导求取(h=1):

黄宁然,数学不好,真的是硬伤。多元泰勒展开,完全不会整,只会勉强整个一元的。详细看文献[3]。
将上述f的表达式写成矩阵[4],
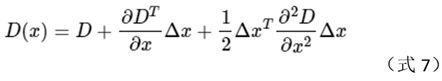
这里,个人觉得文献[4]使用∆x比其它文献里使用X更为合适。
对式(7)求导数,并令等式为0,得到的值就是极值点位置的偏移量,怎么推导,我不会。
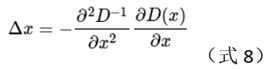
对应极值点处f的值为
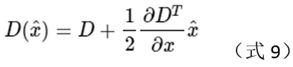
则精确的极值点位置为:
![]()
注意:
在插值极值点时,如果求出∆x的每个维度(即x,y, σ)都小于0.5,则认为插值成功;如果有维度超过0.5,则认为真正的极值点位置更靠近其它临近点,需要更新 X 0 X_0 X0的位置重新进行插值。尝试次数设置为5次,并且如果得出的位置已经超过图像边界,直接认为插值失败[2]。
4.4 边缘响应的剔除[1]
按上述获得的极值点,有一部分是图像的边缘,而SIFT算法更关注的是角状的特征点。所以需要将边缘特征点剔除。
借助Hessian矩阵来剔除边缘响应点。
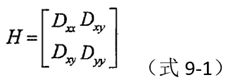
其中,Dxx、Dxy、Dyx、Dyy分别是DoG尺度空间图像在x、y轴方向上的偏导数。
剔除的思想依据:边缘处的H矩阵,其特征值呈一大一小的分布[2]。
令该矩阵的迹和行列式分别为Tr、Det。假设H的两个特征值分别为α、β,则有:
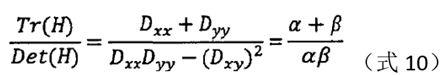
假设是α较大的特征值,β是较小的特征值,令α=r*β,
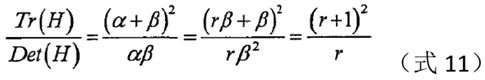
当等式右边越大,两个特征值的差距就越大,即在某个方向上的梯度值较大,而在另一个方向上的梯度值较小,这是边缘的特征,故可删除。对于满足下式(12)的极值点,予以保留,否则,予以剔除。
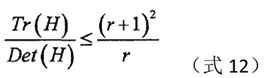
Lowe在论文中,取r为10。
注:该节中的公式如何推导,我不会,数学不好。
4.5 python代码
(1)构建高斯差分层
###################################################### 3. 寻找初始极值点 ##################################################
def construct_DOG(pyr):
dog_pyr=[]
for i in range(len(pyr)):#对于每一组高斯层
octave = pyr[i] #获取当前组
dog=[]
for j in range(len(octave)-1):#对于当前层
diff = octave[j+1]-octave[j]
dog.append(diff)
dog_pyr.append(dog)
return dog_pyr
(2)求取关键点
def get_keypoints(gau_pyr,dog_pyr,sift:CSift):
key_points = []
threshold = np.floor(0.5 * sift.contrast_t / sift.num_scale * 255) #原始图像灰度范围[0,255]
for octave_index in range(len(dog_pyr)):#遍历每一个DoG组
octave = dog_pyr[octave_index]#获取当前组下高斯差分层list
for s in range(1,len(octave)-1):#遍历每一层(第1层到倒数第2层)
bot_img,mid_img,top_img = octave[s-1],octave[s],octave[s+1] #获取3层图像数据
board_width = 5
x_st ,y_st= board_width,board_width
x_ed ,y_ed = bot_img.shape[0]-board_width,bot_img.shape[1]-board_width
for i in range(x_st,x_ed):#遍历中间层图像的所有x
for j in range(y_st,y_ed):#遍历中间层图像的所有y
flag = is_extreme(bot_img[i-1:i+2,j-1:j+2],mid_img[i-1:i+2,j-1:j+2],top_img[i-1:i+2,j-1:j+2],threshold)#初始判断是否为极值
if flag:#若初始判断为极值,则尝试拟合获取精确极值位置
reu = try_fit_extreme(octave,s,i,j,board_width,octave_index,sift)
if reu is not None:#若插值成功,则求取方向信息,
kp,stemp = reu
kp_orientation = compute_orientation(kp,octave_index,gau_pyr[octave_index][stemp],sift)
for k in kp_orientation:#将带方向信息的关键点保存
key_points.append(k)
return key_points
注意,这里获取关键点后,会计算关键点的方位,这在下节中介绍。
def is_extreme(bot,mid,top,thr):
c = mid[1][1]
temp = np.concatenate([bot,mid,top],axis=0)
if c>thr:
index1 = temp>c
flag1 = len(np.where(index1 == True)[0]) > 0
return not flag1
elif c<-thr:
index2 = temp<c
flag2 = len(np.where(index2 == True)[0]) > 0
return not flag2
return False
def try_fit_extreme(octave,s,i,j,board_width,octave_index,sift:CSift):
flag = False
# 1. 尝试拟合极值点位置
for n in range(5):# 共计尝试5次
bot_img, mid_img, top_img = octave[s - 1], octave[s], octave[s + 1]
g,h,offset = fit_extreme(bot_img[i - 1:i + 2, j - 1:j + 2], mid_img[i - 1:i + 2, j - 1:j + 2],top_img[i - 1:i + 2, j - 1:j + 2])
if(np.max(abs(offset))<0.5):#若offset的3个维度均小于0.5,则成功跳出
flag = True
break
s,i,j=round(s+offset[2]),round(i+offset[1]),round(j+offset[0])#否则,更新3个维度的值,重新尝试拟合
if i<board_width or i>bot_img.shape[0]-board_width or j<board_width or j>bot_img.shape[1]-board_width or s<1 or s>len(octave)-2:#若超出边界,直接退出
break
if not flag:
return None
# 2. 拟合成功,计算极值
ex_value = mid_img[i,j]/255+0.5*np.dot(g, offset)#求取经插值后的极值
if np.abs(ex_value)*sift.num_scale<sift.contrast_t: #再次进行弱响应剔除
return None
# 3. 消除边缘响应
hxy=h[0:2,0:2] #获取关于x、y的hessian矩阵
trace_h = np.trace(hxy) #求取矩阵的迹
det_h = det(hxy) #求取矩阵的行列式
# 若hessian矩阵的特征值满足条件(认为不是边缘)
if det_h>0 and (trace_h**2/det_h)<((sift.eigenvalue_r+1)**2/sift.eigenvalue_r):
kp = cv2.KeyPoint()
kp.response = abs(ex_value)#保存响应值
i,j = (i+offset[1]),(j+offset[0])#更新精确x、y位置
kp.pt = j/bot_img.shape[1],i/bot_img.shape[0] #这里保存坐标的百分比位置,免去后续在不同octave上的转换
kp.size = sift.sigma*(2**( (s+offset[2])/sift.num_scale) )* 2**(octave_index)# 保存sigma(o,s)
kp.octave = octave_index + s * (2 ** 8) + int(round((offset[2] + 0.5) * 255)) * (2 ** 16)# 低8位存放octave的index,中8位存放s整数部分,剩下的高位部分存放s的小数部分
return kp,s
return None
def fit_extreme(bot,mid,top):#插值求极值
arr = np.array([bot,mid,top])/255
g = get_gradient(arr)
h = get_hessian(arr)
rt = -lstsq(h, g, rcond=None)[0]#求解方程组
return g,h,rt
def get_gradient(arr): #获取一阶梯度
dx = (arr[1,1,2]-arr[1,1,0])/2
dy = (arr[1,2,1] - arr[1,0,1])/2
ds = (arr[2,1,1] - arr[0,1,1])/2
return np.array([dx, dy, ds])
def get_hessian(arr): #获取三维hessian矩阵
dxx = arr[1,1,2]-2*arr[1,1,1] + arr[1,1,0]
dyy = arr[1,2,1]-2*arr[1,1,1] + arr[1,0,1]
dss = arr[2,1,1]-2*arr[1,1,1] + arr[0,1,1]
dxy = 0.25*( arr[1,0,0]+arr[1,2,2]-arr[1,0,2] - arr[1,2,0] )
dxs = 0.25*( arr[0,1,0]+arr[2,1,2] -arr[0,1,2] - arr[2,1,0])
dys = 0.25*( arr[0,0,1]+arr[2,2,1]- arr[0,2,1] -arr[2,0,1])
return np.array([[dxx,dxy,dxs],[dxy,dyy,dys],[dxs,dys,dss]])
5.计算极值点(关键点)方向
上节中,通过对比不同尺度下的像素值,得到极值点,这些极值点已具备尺度不变性的稳定特征[2]。接下来求取方位信息。说到方位,自然想到梯度角。
中心思想:通过计算极值点周围邻域的梯度模和梯度角度,给每个极值点分配方向。为什么要计算邻域而不是直接极值点位置对应梯度?为了综合考虑,提高鲁棒性。为什么要梯度模信息?梯度模过小,认为弱响应,会被剔除。
5.1 计算步骤
梯度的求取是在与极值点对应的高斯层G(o,s)上进行的。具体步骤:
(1)找到与极值点位置(o,s)最接近的高斯层,以该层图像作为输入
(2)在该层图像中,选取极值点位置(x,y)的邻域。邻域半径按下式进行确定[8]
r = 3 ∗ 1.5 ∗ σ r=3*1.5*σ r=3∗1.5∗σ (式13)
式中,3表示按尺度采样的3倍原则[3],1.5为尺度系数,σ为极值点所在(o,s)下的尺度
(3)对邻域内的所有点,求取梯度模和梯度角。
梯度模和梯度角的计算公式:
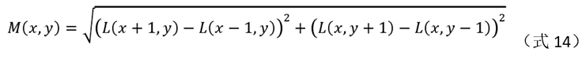

公式中L是高斯层图像。
(4)方位分配及模值累加
SIFT算法将360°方位平分为36个方向组,每个方向组跨越10°。将第3步求出的梯度模,依据梯度角分配到这36个方向组中,并将每个方向组中的梯度模进行累加求和。这里,梯度模进行累加求和时,需要进行高斯加权运算,简单说,邻域中,离极值点远的模值具有较小贡献,离极值点近的模值具有较大贡献。
高斯加权运算中,高斯函数的标准差为当前尺度的1.5倍。高斯加权系数:
![]()
经过这一步骤,36个方向组的数组histogram内便保存着相应的梯度模的累加和,形状像是直方图。
(5)平滑滤波
对第(4)步骤形成的histogram进行平滑滤波,滤波公式如下:
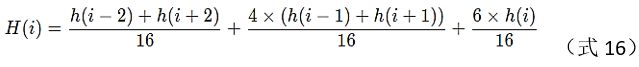
(6)生成主方向和辅方向
一般来说,对于第(5)步得到的histogram数组,找到其最大值所在位置,该位置对应的方向组,即可作为该极值点的方向。而在实际操作过程中,为了保证算法鲁棒性,算法除了保留最大值位置所在的方向(作为主方向),还保留了幅值大于最大值80%位置所在的方向,作为辅方向。具体操作:首先找到histogram数组的最大值max_v;然后,找出histogram数组所有的局部极大值点;对于每一个局部极大值peak_v,如果其大于80%*max_v,则结合其左、右两点left_v、right_v,共计3点,进行抛物线二次插值,得到精确的极大值的位置,该位置折算得到的方向,即作为该极值点的主/辅方向,即第4章节中,一个极值点,会对应多个方向信息,形成多个关键点。精确极大值位置的求取,可根据初中数学知识,文献[3]给出了详细说明。
设抛物线:
![]()
将每个极大值位置i归一到0处,则有
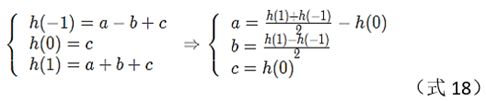
则精确的极大值位置为:
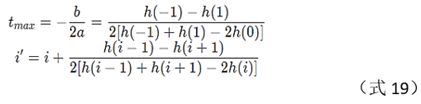
5.2 python代码
###################################################### 4. 计算方位信息 ##################################################
def compute_orientation(kp,octave_index,img,sift:CSift):
keypoints_with_orientations = []
cur_scale = kp.size / (2**(octave_index)) #除去组信息o,不知为何?莫非因为输入图像img已经是进行了降采样的图像,涵盖了o的信息?
radius = round(sift.radius_factor*sift.scale_factor*cur_scale)#求取邻域半径
weight_sigma = -0.5 / ((sift.scale_factor*cur_scale) ** 2)#高斯加权运算系数
raw_histogram = np.zeros(sift.num_bins)#初始化方位数组
cx = round( kp.pt[0]*img.shape[1] )#获取极值点位置x
cy = round( kp.pt[1]*img.shape[0] )#获取极值点位置y
# 1.计算邻域内所有点的梯度值、梯度角,并依据梯度角将梯度值分配到相应的方向组中
for y in range(cy-radius, cy+radius + 1): # 高,对应行
for x in range(cx-radius, cx+radius + 1):# 宽,对应列
if y > 0 and y < img.shape[0] - 1 and x > 0 and x < img.shape[1] - 1 :
dx = img[y, x + 1] - img[y, x - 1]
dy = img[y - 1, x] - img[y + 1, x]
mag = np.sqrt(dx ** 2 + dy ** 2)#计算梯度模
angle = np.rad2deg(np.arctan2(dy, dx))#计算梯度角
if angle < 0:
angle = angle + 360
angle_index = round(angle / (360 / sift.num_bins))
angle_index = angle_index % sift.num_bins
weight = np.exp(weight_sigma * ((y-cy)**2 +(x-cx)**2 ))#根据x、y离中心点的位置,计算权重
raw_histogram[angle_index] = raw_histogram[angle_index] + mag * weight#将模值分配到相应的方位组上
# 2. 对方向组直方图进行平滑滤波
h = raw_histogram
ha2 = np.append(h[2:],(h[0],h[1])) # np.roll will be better
hm2 = np.append((h[-2],h[-1]),h[:-2])
ha1 = np.append(h[1:], h[0])
hm1 = np.append(h[-1], h[:-1])
smooth_histogram = ( ha2+hm2 + 4*(ha1+hm1) + 6*h)/16
# 3. 计算极值点的主方向和辅方向
s = smooth_histogram
max_v = max(s)# 找最大值
s1 = np.roll(s,1)
s2 = np.roll(s,-1)
index1 = s>=s1
index2 = s>=s2
index = np.where( np.logical_and(index1,index2)==True )[0] #找到所有极值点位置
for i in index:
peak_v = s[i]
if peak_v >= sift.peak_ratio * max_v: #若大于阈值,则保留,作为主/辅方向
left_v = s[(i-1)%sift.num_bins]
right_v = s[(i+1)%sift.num_bins]
index_fit= ( i+0.5*(left_v-right_v)/(left_v+right_v-2*peak_v) )%sift.num_bins#插值得到精确极值位置
angle = 360-index_fit/sift.num_bins*360 #计算精确的方位角
new_kp =cv2.KeyPoint(*kp.pt, kp.size, angle, kp.response, kp.octave) #在关键点中,加入方向信息
keypoints_with_orientations.append(new_kp)
return keypoints_with_orientations
6.极值点(关键点)的特征描述
上节中,已经得到了关键点的位置信息、方位信息。已解决关键点的尺度不变性。但是,旋转不变性、亮度不变性尚未解决。接下来,会为上节的每一个关键点,生成相应的特征描述符,并保证旋转不变性、亮度不变性。
同样,为了保证鲁棒性,生成描述符时,不仅仅考虑关键点信息,还考虑关键点所在的邻域信息,这与在上节中求取极值点的方向时类似。据文献[1],特征描述符与关键点所在尺度有关,所有特征描述符的求取在高斯尺度图像上进行。
6.1邻域的选择
据文献[1],原作Lowe将关键点的邻域划分为4×4个子区域,而每个子区域具有8个方向信息(即将360度8等分),所以,每个关键点最终会得到4*4*8=128维的描述。
对于4×4的子区域,每个子区域是边长为3*σ的正方形,其中,σ是当前关键点所在的尺度。邻域的选择如图5所示。

在图5中左边部分,中心的黑点即是关键点位置,绿色部分的窗口,为d×d个子区域,这里d=4,每个绿色方框的边长为3*σ。邻域半径为 √ 2 × ( 0.5 × d × 3 × σ ) √2×(0.5×d×3×σ) √2×(0.5×d×3×σ),实际,按下式计算:

描述符的确定即是:计算关键点周围的4×4个子区域、在8方位组上的模值,即图5的右边部分。
6.2坐标轴旋转
每个关键点是有方向信息的,在确定邻域后,将整个坐标轴旋转,使得坐标轴与关键点的方向重合。旋转后的坐标计算公式如下:
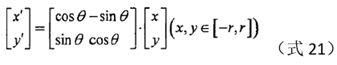
上式中的θ即是关键点方向角的负数。
为什么要旋转使得坐标轴方向与关键点方向重合?个人理解,类似于幅值的归一化,将每个关键点的方向信息归一到0度,这样保证旋转不变性。
6.3 计算邻域内各点的梯度
计算邻域内每个点的梯度,包括梯度值、梯度方向,然后:
(1)根据每个点的位置(x,y),计算所处4×4小窗口的下标(r,c);
(2)根据每个点的梯度方向,计算所处的方向组下标o(8个方向组中的一个)
(3)计算梯度值,并根据每个点的位置,将梯度值乘以加权系数,得到m。这里采用高斯加权运算中,文献[3]描述,Lowe建议高斯函数的标准差为0.5×d。
6.4 各点梯度值的分配
梯度值的分配,即是把上节求出的梯度值m,依据下标(r,c,o),分配到4×4×8中的某一个,因为上节中的(r,c,o)是带小数的,这里使用线性插值,来分配到4×4×8中。以r维度来举例说明,如图6。
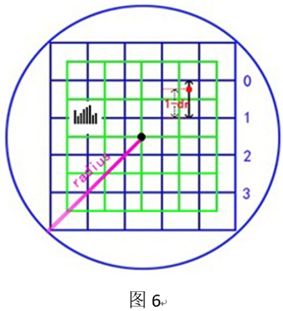
在图6中,假设邻域中某点的位置如图中的红色点,在r维度上,其处于第0行和第1行之间,所以其对[0,3]和[1,3]这2个小窗口都有贡献。仅考虑r维度,假设r的小数部分为dr,则dr越大,越偏离0行,对0行贡献越小,对1行贡献越大。所以根据距离,使用线性插值,红色点对0行的贡献C0=(1-dr)*m,对1行的贡献为C1=dr*m。
然后,再考虑c维度,红色点还处于第2列和第3列之间,所以使用同样方法,分别对C0和C1在列维度上的贡献进行插值,得到C00、C01和C10、C11(注意,这里下标0表示向下取整后的下标,1表示向上取整后的下标)。
然后,再考虑方向组o维度,依次得到C000、C001…C110、C111,共计3个维度8个分量。
经过上述,就将梯度幅度分配到4×4×8中了。
6.5 归一化
归一化的目的是保证算法的亮度不变性。归一化公式如下:
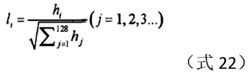
其中,h即是上节中求取的128维向量。Rmislam[6]在代码中,使用的是范数。同时,为了消除极大值的影响,据文献[2]描述,Lowe将归一化向量中阈值超过0.2的分量置为0.2。
6.6 python代码
#################################################### 5. 计算关键点的特征描述符 #############################################
def get_descriptor(kps,gau_pyr,win_N=4, num_bins=8, scale_multiplier=3, des_max_value=0.2):
descriptors = []
for kp in kps:
octave, layer =kp.octave & 255 , (kp.octave >> 8)&255
image = gau_pyr[octave][layer]
img_rows,img_cols = image.shape
bins_per_degree = num_bins / 360.
angle = 360. - kp.angle #旋转角度为关键点方向角的负数
cos_angle = np.cos(np.deg2rad(angle))
sin_angle = np.sin(np.deg2rad(angle))
weight_multiplier = -0.5 / ((0.5 * win_N) ** 2)#高斯加权运算,方差为0.5×d
row_bin_list = []#存放每个邻域点对应4×4个小窗口中的哪一个(行)
col_bin_list = []#存放每个邻域点对应4×4个小窗口中的哪一个(列)
magnitude_list = []#存放每个邻域点的梯度幅值
orientation_bin_list = []#存放每个邻域点的梯度方向角所处的方向组
histogram_tensor = np.zeros((win_N + 2, win_N + 2, num_bins))#存放4×4×8个描述符,但为防止计算时边界溢出,在行、列的首尾各扩展一次
hist_width = scale_multiplier * kp.size/(2**(octave)) # 3×sigma,每个小窗口的边长
radius = int(round(hist_width * np.sqrt(2) * (win_N + 1) * 0.5))
radius = int(min(radius, np.sqrt(img_rows ** 2 + img_cols ** 2)))
for row in range(-radius, radius + 1):
for col in range(-radius, radius + 1):
row_rot = col * sin_angle + row * cos_angle#计算旋转后的坐标
col_rot = col * cos_angle - row * sin_angle#计算旋转后的坐标
row_bin = (row_rot / hist_width) + 0.5 * win_N - 0.5 #对应4×4子区域的下标(行)
col_bin = (col_rot / hist_width) + 0.5 * win_N - 0.5#对应在4×4子区域的下标(列)
if row_bin > -1 and row_bin < win_N and col_bin > -1 and col_bin < win_N:#邻域的点在旋转后,仍然处于4×4的区域内,
window_row = int(round(kp.pt[1]*image.shape[0] + row))#计算对应原图的row
window_col = int(round(kp.pt[0]*image.shape[1] + col))#计算对应原图的col
if window_row > 0 and window_row < img_rows - 1 and window_col > 0 and window_col < img_cols - 1:
dx = image[window_row, window_col + 1] - image[window_row, window_col - 1]#直接在旋转前的图上计算梯度,因为旋转时,都旋转了,不影响大小
dy = image[window_row - 1, window_col] - image[window_row + 1, window_col]#直接在旋转前的图上计算梯度,因为旋转时,都旋转了,不影响大小
gradient_magnitude = np.sqrt(dx * dx + dy * dy)
gradient_orientation = np.rad2deg(np.arctan2(dy, dx)) % 360
weight = np.exp(weight_multiplier * ((row_rot / hist_width) ** 2 + (col_rot / hist_width) ** 2))#不明白为什么要处以小窗口的边长,是要以边长为单位?
row_bin_list.append(row_bin)
col_bin_list.append(col_bin)
magnitude_list.append(weight * gradient_magnitude)
orientation_bin_list.append((gradient_orientation - angle) * bins_per_degree)#因为梯度角是旋转前的,所以还要叠加上旋转的角度
#将magnitude分配到4*4*8(d*d*num_bins)的各区域中,即分配到histogram_tensor数组中
for r,c,o,m in zip(row_bin_list,col_bin_list,orientation_bin_list,magnitude_list):
ri,ci,oi = np.floor([r,c,o]).astype(int)
rf,cf,of = [r,c,o]-np.array([ri,ci,oi]) #rf越大,越偏离当前行,同理cf,of
#先按行分解
c0 = m*(1-rf)#当前行的分量
c1 = m*rf #下一行的分量
#对每一个行分量,按列分解
c00 = c0*(1-cf)#当前行、当前列
c01 = c0*cf##当前行、下一列
c10 = c1*(1-cf)#下一行、当前列
c11=c1*cf#下一行、下一列
#对每一个行+列分量,按方向角分解
c000, c001 = c00*(1-of),c00*of
c010, c011= c01*(1-of),c01*of
c100,c101 = c10*(1-of), c10*of
c110,c111 = c11*(1-of),c11*of
# 数值填入到数组中
histogram_tensor[ri+1,ci+1,oi] += c000
histogram_tensor[ri + 1, ci + 1, (oi+1)%num_bins] += c001
histogram_tensor[ri + 1, ci + 2, oi] += c010
histogram_tensor[ri + 1, ci + 2, (oi + 1) % num_bins] += c011
histogram_tensor[ri + 2, ci + 1, oi] += c100
histogram_tensor[ri + 2, ci + 1, (oi + 1) % num_bins] += c101
histogram_tensor[ri + 2, ci + 2, oi] += c110
histogram_tensor[ri + 2, ci + 2, (oi + 1) % num_bins] += c111
des_vec = histogram_tensor[1:-1,1:-1,:].flatten()#转成一维向量形式
#des_vec[des_vec > des_max_value*np.linalg.norm(des_vec)] = des_max_value*np.linalg.norm(des_vec)
#des_vec = des_vec / np.linalg.norm(des_vec)
des_vec = des_vec/np.linalg.norm(des_vec)
des_vec[des_vec>des_max_value] = des_max_value
des_vec = np.round(512*des_vec)
des_vec[des_vec<0]=0
des_vec[des_vec>255]=255
descriptors.append(des_vec)
return descriptors
def sort_method(kp1:cv2.KeyPoint,kp2:cv2.KeyPoint):
if kp1.pt[0] != kp2.pt[0]:
return kp1.pt[0] - kp2.pt[0]
if kp1.pt[1] != kp2.pt[1]:
return kp1.pt[1] - kp2.pt[1]
if kp1.size != kp2.size:
return kp1.size - kp2.size
if kp1.angle != kp2.angle:
return kp1.angle - kp2.angle
if kp1.response != kp2.response:
return kp1.response - kp2.response
if kp1.octave != kp2.octave:
return kp1.octave - kp2.octave
return kp1.class_id - kp2.class_id
def remove_duplicate_points(keypoints):
keypoints.sort(key=cmp_to_key(sort_method))
unique_keypoints = [keypoints[0]]
for next_keypoint in keypoints[1:]:
last_unique_keypoint = unique_keypoints[-1]
if last_unique_keypoint.pt[0] != next_keypoint.pt[0] or \
last_unique_keypoint.pt[1] != next_keypoint.pt[1] or \
last_unique_keypoint.size != next_keypoint.size or \
last_unique_keypoint.angle != next_keypoint.angle:
unique_keypoints.append(next_keypoint)
return unique_keypoints
7.特征描述符的匹配
经过上节处理,即得到图像的关键点的特征描述符。在得到2张图的关键点特征描述符后,即可进行描述符匹配。对于2个关键点描述符,通过判断其欧式距离的大小,来判断匹配的成功与否[2];对于2幅图的所有关键点描述符,使用穷举匹配或聚类匹配。
使用opencv的FlannBasedMatcher.knnMatch()函数对2幅图的特征描述符进行匹配。该函数的用法,参考文献[9]以及文献[9]的评论区(高手都在评论区)。
Python代码如下:
#################################################### 6. 匹配 ############################################################
def do_match(img_src1,kp1,des1,img_src2,kp2,des2,embed=1,pt_flag=0,MIN_MATCH_COUNT = 10):
## 1. 对关键点进行匹配 ##
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
search_params = dict(checks=50)
flann = cv2.FlannBasedMatcher(index_params, search_params)
des1, des2 = np.array(des1).astype(np.float32), np.array(des2).astype(np.float32)#需要转成array
matches = flann.knnMatch(des1, des2, k=2) # matches为list,每个list元素由2个DMatch类型变量组成,分别是最邻近和次邻近点
good_match = []
for m in matches:
if m[0].distance < 0.7 * m[1].distance: # 如果最邻近和次邻近的距离差距较大,则认可
good_match.append(m[0])
## 2. 将2张图画在同一张图上 ##
img1 = img_src1.copy()
img2 = img_src2.copy()
h1, w1 = img1.shape[0],img1.shape[1]
h2, w2 = img2.shape[0],img2.shape[1]
new_w = w1 + w2
new_h = np.max([h1, h2])
new_img = np.zeros((new_h, new_w,3), np.uint8) if len(img_src1.shape)==3 else np.zeros((new_h, new_w), np.uint8)
h_offset1 = int(0.5 * (new_h - h1))
h_offset2 = int(0.5 * (new_h - h2))
if len(img_src1.shape) == 3:
new_img[h_offset1:h_offset1 + h1, :w1,:] = img1 # 左边画img1
new_img[h_offset2:h_offset2 + h2, w1:w1 + w2,:] = img2 # 右边画img2
else:
new_img[h_offset1:h_offset1 + h1, :w1] = img1 # 左边画img1
new_img[h_offset2:h_offset2 + h2, w1:w1 + w2] = img2 # 右边画img2
##3. 两幅图存在足够的匹配点,两幅图匹配成功,将匹配成功的关键点进行连线 ##
if len(good_match) > MIN_MATCH_COUNT:
src_pts = []
dst_pts = []
mag_err_arr=[]
angle_err_arr=[]
for m in good_match:
if pt_flag==0:#point是百分比
src_pts.append([kp1[m.queryIdx].pt[0] * img1.shape[1], kp1[m.queryIdx].pt[1] * img1.shape[0]])#保存匹配成功的原图关键点位置
dst_pts.append([kp2[m.trainIdx].pt[0] * img2.shape[1], kp2[m.trainIdx].pt[1] * img2.shape[0]])#保存匹配成功的目标图关键点位置
else:
src_pts.append([kp1[m.queryIdx].pt[0], kp1[m.queryIdx].pt[1]]) # 保存匹配成功的原图关键点位置
dst_pts.append([kp2[m.trainIdx].pt[0], kp2[m.trainIdx].pt[1]]) # 保存匹配成功的目标图关键点位置
mag_err = np.abs(kp1[m.queryIdx].response - kp2[m.trainIdx].response) / np.abs(kp1[m.queryIdx].response )
angle_err = np.abs(kp1[m.queryIdx].angle - kp2[m.trainIdx].angle)
mag_err_arr.append(mag_err)
angle_err_arr.append(angle_err)
if embed!=0 :#若图像2是图像1内嵌入另一个大的背景中,则在图像2中,突出显示图像1的边界
M = cv2.findHomography(np.array(src_pts), np.array(dst_pts), cv2.RANSAC, 5.0)[0] # 根据src和dst关键点,寻求变换矩阵
src_w, src_h = img1.shape[1], img1.shape[0]
src_rect = np.array([[0, 0], [src_w - 1, 0], [src_w - 1, src_h - 1], [0, src_h - 1]]).reshape(-1, 1, 2).astype(
np.float32) # 原始图像的边界框
dst_rect = cv2.perspectiveTransform(src_rect, M) # 经映射后,得到dst的边界框
img2 = cv2.polylines(img2, [np.int32(dst_rect)], True, 255, 3, cv2.LINE_AA) # 将边界框画在dst图像上,突出显示
if len(new_img.shape) == 3:
new_img[h_offset2:h_offset2 + h2, w1:w1 + w2,:] = img2 # 右边画img2
else:
new_img[h_offset2:h_offset2 + h2, w1:w1 + w2] = img2 # 右边画img2
new_img = new_img if len(new_img.shape) == 3 else cv2.cvtColor(new_img, cv2.COLOR_GRAY2BGR)
# 连线
for pt1, pt2 in zip(src_pts, dst_pts):
cv2.line(new_img, tuple(np.int32(np.array(pt1) + [0, h_offset1])),
tuple(np.int32(np.array(pt2) + [w1, h_offset2])), color=(0, 0, 255))
return new_img
8.测试结果
python程序:
def do_sift(img_src,sift:CSift):
img = img_src.copy().astype(np.float32)
img = pre_treat_img(img,sift.sigma)
sift.num_octave = get_numOfOctave(img)
gaussian_pyr = construct_gaussian_pyramid(img,sift)
dog_pyr = construct_DOG(gaussian_pyr)
key_points = get_keypoints(gaussian_pyr,dog_pyr,sift)
key_points = remove_duplicate_points(key_points)
descriptor = get_descriptor(key_points,gaussian_pyr)
return key_points,descriptor
if __name__ == '__main__':
MIN_MATCH_COUNT = 10
sift = CSift(num_octave=4,num_scale=3,sigma=1.6)
img_src1 = cv2.imread('box.png',-1)
#img_src1 = cv2.resize(img_src1, (0, 0), fx=.25, fy=.25)
img_src2 = cv2.imread('box_in_scene.png', -1)
#img_src2 = cv2.resize(img_src2, (0, 0), fx=.5, fy=.5)
# 1. 使用本sift算子
kp1, des1 = do_sift(img_src1, sift)
kp2, des2 = do_sift(img_src2, sift)
pt_flag = 0
'''
# 3. 做匹配
reu_img = do_match(img_src1, kp1, des1, img_src2, kp2, des2, embed=1, pt_flag=pt_flag,MIN_MATCH_COUNT=3)
cv2.imshow('reu',reu_img)
cv2.imwrite('reu.tif',reu_img)
注:运行很耗时间,很慢,很慢,犹如以前的车马,请耐心等待。
使用box图像测试

9.基于opencv实现SIFT
Opencv内集成了SIFT算法。在此,使用的Opencv-python版本为4.4.0.42。使用方法也就3步骤:
opencv_sift = cv2.SIFT.create(nfeatures=None, nOctaveLayers= None,
contrastThreshold= None, edgeThreshold= None , sigma= None )
kp1 = opencv_sift.detect(img_src1)
kp1,des1 = opencv_sift.compute(img_src1,kp1)
在create算子时,填好相关参数。Opencv自带的sift算子,运算速度超级快,获得的结果也比手动编写的多(可能与参数有关)。其返回的kp是keypoint类,包含了每个关键点的位置、方位、响应值(梯度值)等信息。
python代码:
if __name__ == '__main__':
MIN_MATCH_COUNT = 10
sift = CSift(num_octave=4,num_scale=3,sigma=1.6)
img_src1 = cv2.imread('box.png',-1)
#img_src1 = cv2.resize(img_src1, (0, 0), fx=.25, fy=.25)
img_src2 = cv2.imread('box_in_scene.png', -1)
#img_src2 = cv2.resize(img_src2, (0, 0), fx=.5, fy=.5)
# 2. 使用opencv自带sift算子
sift.num_octave = get_numOfOctave(img_src1)
opencv_sift = cv2.SIFT.create(nfeatures=None, nOctaveLayers=sift.num_octave,
contrastThreshold=sift.contrast_t, edgeThreshold=sift.eigenvalue_r, sigma=sift.sigma)
kp1 = opencv_sift.detect(img_src1)
kp1,des1 = opencv_sift.compute(img_src1,kp1)
sift.num_octave = get_numOfOctave(img_src2)
opencv_sift = cv2.SIFT.create(nfeatures=None, nOctaveLayers=sift.num_octave,
contrastThreshold=sift.contrast_t, edgeThreshold=sift.eigenvalue_r, sigma=sift.sigma)
kp2 = opencv_sift.detect(img_src2)
kp2, des2 = opencv_sift.compute(img_src2, kp2)
pt_flag = 1
# 3. 做匹配
reu_img = do_match(img_src1, kp1, des1, img_src2, kp2, des2, embed=1, pt_flag=pt_flag,MIN_MATCH_COUNT=3)
cv2.imshow('reu',reu_img)
cv2.imwrite('reu.tif',reu_img)
测试结果:

所以,呃呃,为何要自己动手写代码实现,何必跟自己过不去。
10.关于问题
相机置于地面,离天花板的高度始终不变。在某位置抵对着天花板拍一张图,然后相机移动一定距离、旋转一定角度后再拍一张图。这2张图上的特征点,在梯度值和梯度方向上是否一致呢?
10.1 仅旋转一定角度且相机水平
在相机是水平的前提下,如果相机仅仅是旋转了一定角度,则理论上,第二张图也是第一张图旋转该角度后的结果。因此,2张图上特征点的梯度值的大小是不会变化的,但是梯度方向会发生变化,差值为该旋转角度。
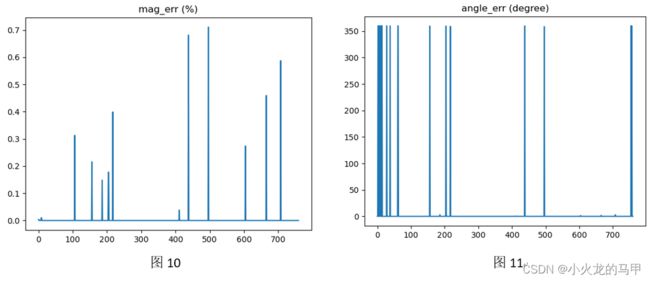
使用图片进行旋转测试。为防止opencv在旋转图片时会对图片进行插值造成的像素值变化,这里,旋转角度为90度,且直接使用矩阵运算进行旋转。将2幅图分别调用opencv的sift算法,求得关键点、描述符,再进行匹配。匹配过程中,保存匹配成功的关键点在梯度值、梯度方向上的误差,梯度值误差为相对误差,梯度方向误差为绝对误差。结果如下图所示。

测试结果可看出,梯度幅值误差基本在2%以内,梯度方向误差,基本在270度上下。在图7、8中,第2点、第4点有明显异常跳变,寻找下原因:关键点匹配时匹配错位,如图9所示。

在图9中,蓝线是梯度值误差最大的2个;红线是梯度值误差最小的5个。可见,蓝线出现位置点匹配错误的情况,因而自然会出现梯度值误差较大的情况。
10.2 仅移动一定距离且相机水平
在相机是水平的前提下,相机移动移动距离,相当于旧的景色移出、新的景色移入。这时,前后2张图,关键点的梯度值、梯度方向理论上均不变。
使用图片进行移入移出测试,且直接使用矩阵运算,不改变像素值。将2幅图按上节同样方法进行处理。结果如下图所示。

可见,梯度值误差很小,梯度方向一致(0或360度)。
10.3 相机不水平
若相机在视野内不是绝对水平(例如,与天花板有倾斜角度 ),则相机移动、旋转应该都会导致梯度值的变化,因为关键点周围的像素发生了变化,而梯度值在求取时,是极值点r半径内所有邻域的综合结果,这个r还与尺度有关。对梯度值的变化影响到底有多大,与相机的不水平程度、移动距离、旋转角度有关。
使用仿射变换来模拟相机不水平情况下、进行移动、旋转后的成像。将2幅图按上节同样方法进行处理。结果如下图所示。
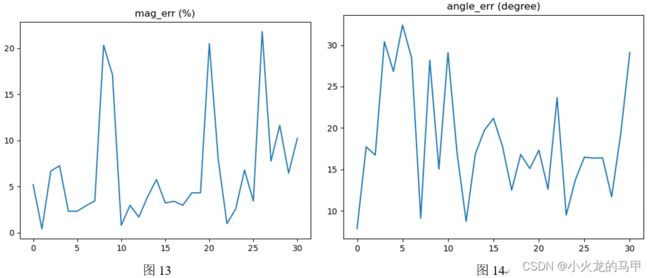

可见,梯度值的误差明显变大。但这样也不能确切的说明什么,毕竟在进行仿射变换时,已经进行插值处理,修改了图像像素,另外,关键点的匹配是否精确,也需要考究。
本节测试的python代码:
#################################################### 7. 测试移动和旋转 ####################################################
def move_rotate_sift_test():
img_src = cv2.imread('box.png', 0)
img_src1 = img_src.copy()
#### 情形1.旋转90度 ###
img_src2 = img_src1.transpose()
img_src2 = np.fliplr(img_src2)
#### 情形2. 景色移出视野 ###
img_src2 = img_src1[:,50:]
#### 情形3. 放射变换 ###
points1 = np.float32([[81, 30], [378, 80], [13, 425]])
points2 = np.float32([[0, 0], [300, 0], [100, 300]])
affine_matrix = cv2.getAffineTransform(points1, points2)
img_src2 = cv2.warpAffine(img_src1, affine_matrix, (0, 0), flags=cv2.INTER_CUBIC,
borderMode=cv2.BORDER_CONSTANT, borderValue=0)
#### 做sift ####
sift.num_octave = get_numOfOctave(img_src1)
opencv_sift = cv2.SIFT.create(nfeatures=None, nOctaveLayers=sift.num_octave,
contrastThreshold=sift.contrast_t, edgeThreshold=sift.eigenvalue_r, sigma=sift.sigma)
kp1 = opencv_sift.detect(img_src1)
kp1, des1 = opencv_sift.compute(img_src1, kp1)
sift.num_octave = get_numOfOctave(img_src2)
opencv_sift = cv2.SIFT.create(nfeatures=None, nOctaveLayers=sift.num_octave,
contrastThreshold=sift.contrast_t, edgeThreshold=sift.eigenvalue_r, sigma=sift.sigma)
kp2 = opencv_sift.detect(img_src2)
kp2, des2 = opencv_sift.compute(img_src2, kp2)
reu_img = do_match_compare(img_src1, kp1, des1, img_src2, kp2, des2, embed=0, pt_flag=1, MIN_MATCH_COUNT=3)
cv2.imshow('reu', reu_img)
return
def do_match_compare(img_src1,kp1,des1,img_src2,kp2,des2,embed=1,pt_flag=0,MIN_MATCH_COUNT = 10):
## 1. 对关键点进行匹配 ##
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
search_params = dict(checks=50)
flann = cv2.FlannBasedMatcher(index_params, search_params)
des1, des2 = np.array(des1).astype(np.float32), np.array(des2).astype(np.float32)#需要转成array
matches = flann.knnMatch(des1, des2, k=2) # matches为list,每个list元素由2个DMatch类型变量组成,分别是最邻近和次邻近点
good_match = []
for m in matches:
if m[0].distance < 0.5 * m[1].distance: # 如果最邻近和次邻近的距离差距较大,则认可
good_match.append(m[0])
## 2. 将2张图画在同一张图上 ##
img1 = img_src1.copy()
img2 = img_src2.copy()
h1, w1 = img1.shape[0],img1.shape[1]
h2, w2 = img2.shape[0],img2.shape[1]
new_w = w1 + w2
new_h = np.max([h1, h2])
new_img = np.zeros((new_h, new_w), np.uint8)
h_offset1 = int(0.5 * (new_h - h1))
h_offset2 = int(0.5 * (new_h - h2))
new_img[h_offset1:h_offset1 + h1, :w1] = img1 # 左边画img1
new_img[h_offset2:h_offset2 + h2, w1:w1 + w2] = img2 # 右边画img2
##3. 两幅图存在足够的匹配点,两幅图匹配成功,将匹配成功的关键点进行连线 ##
if len(good_match) > MIN_MATCH_COUNT:
src_pts = []
dst_pts = []
mag_err_arr=[] #保存匹配的关键点,在梯度幅值上的相对误差
angle_err_arr=[]#保存匹配的关键点,在梯度方向上的绝对误差
for m in good_match:
if pt_flag==0:#point是百分比
src_pts.append([kp1[m.queryIdx].pt[0] * img1.shape[1], kp1[m.queryIdx].pt[1] * img1.shape[0]])#保存匹配成功的原图关键点位置
dst_pts.append([kp2[m.trainIdx].pt[0] * img2.shape[1], kp2[m.trainIdx].pt[1] * img2.shape[0]])#保存匹配成功的目标图关键点位置
else:
src_pts.append([kp1[m.queryIdx].pt[0], kp1[m.queryIdx].pt[1]]) # 保存匹配成功的原图关键点位置
dst_pts.append([kp2[m.trainIdx].pt[0], kp2[m.trainIdx].pt[1]]) # 保存匹配成功的目标图关键点位置
mag_err = np.abs(kp1[m.queryIdx].response - kp2[m.trainIdx].response) / np.abs(kp1[m.queryIdx].response ) *100
angle_err = (kp1[m.queryIdx].angle - kp2[m.trainIdx].angle)%360
mag_err_arr.append(mag_err)
angle_err_arr.append(angle_err)
new_img = cv2.cvtColor(new_img, cv2.COLOR_GRAY2BGR)
plt.figure()
plt.title('mag_err (%)')
plt.plot(mag_err_arr)
plt.figure()
plt.title('angle_err (degree)')
plt.plot(angle_err_arr)
plt.show()
# 连线
index = np.argsort(mag_err_arr)#进行有小到大排序
for i in range(0,5): #画出误差最小的5个匹配点连线
pt1, pt2 = src_pts[index[i]], dst_pts[index[i]]
cv2.line(new_img, tuple(np.int32(np.array(pt1) + [0, h_offset1])),
tuple(np.int32(np.array(pt2) + [w1, h_offset2])), color=(0, 0, 255))
for i in range(-3, 0):#画出误差最大的3个匹配点连线
pt1, pt2 = src_pts[index[i]], dst_pts[index[i]]
cv2.line(new_img, tuple(np.int32(np.array(pt1) + [0, h_offset1])), tuple(np.int32(np.array(pt2) + [w1, h_offset2])), color=(255, 0, 0))
return new_img
11. 源码下载
https://download.csdn.net/download/xiaohuolong1827/85221790
12.其它
使用其它的图片进行测试。
左边是黄宁然2月份晚上去的,右边是笔者4月份白天去的。去过你去过的地方,看过你看过的风景。那么匹配结果怎么样?


呃,GG。还是要多读书。
本帖,权当乐呵了。