Lesson 11.1-11.5 梯度下降的两个关键问题&反向传播的原理&走出第一步:动量法&开始迭代:batch和epochs&在Fashion—MNIST数据集熵实现完整的神经网络
在之前的课程中,我们已经完成了从0建立深层神经网络,并介绍了各类神经网络所使用的损失函数。本节课开始,我们将以分类深层神经网络为例,为大家展示神经网络的学习和训练过程。在介绍PyTorch的基本工具AutoGrad库时,我们系统地介绍过数学中的优化问题和优化思想,我们介绍了最小二乘法以及梯度下降法这两个入门级优化算法的具体操作,并使用AutoGrad库实现了他们。在本节课中,我们将从梯度下降法向外拓展,介绍更常用的优化算法,实现神经网络的学习和迭代。在本节课结束的时候,你将能够完整地实现一个神经网络训练的全流程。
Lesson 11 神经网络的学习
一 梯度下降中的两个关键问题
1 找出梯度向量的方向和大小
2 让坐标点移动起来(进行一次迭代)
二、找出距离和方向:反向传播
1 反向传播的定义与价值
2 PyTorch实现反向传播
三、移动坐标点
1 走出第一步
2 从第一步到第二步:动量法Momentum
3 torch.optim实现带动量的梯度下降
四、开始迭代:batch_size与epoches
1 为什么要有小批量?
2 batch_size与epoches
3 TensorDataset与DataLoader
五、在MINST-FASHION上实现神经网络的学习流程
1 导库,设置各种初始值
2 导入数据,分割小批量
3 定义神经网络的架构
4 定义训练函数
5 进行训练与评估
在我们的优化流程之中,我们使用损失函数定义预测值与真实值之间的差异,也就是模型的优劣。当损失函数越小,就说明模型的效果越好,我们要追求的时损失函数最小时所对应的权重向量 。对于凸函数而言,导数为0的点就是极小值点,因此在数学中,我们常常先对权重 w w w求导,再令导数为0来求解极值和对应的 w w w。但是对于像神经网络这样的复杂模型,可能会有数百个 w w w的存在,同时如果我们使用的是像交叉熵这样复杂的损失函数(机器学习中还有更多更加复杂的函数),令所有权重的导数为0并一个个求解方程的难度很大、工作量也很大。因此我们转换思路,不追求一步到位,而使用迭代的方式逐渐接近损失函数的最小值。这就是优化算法的具体工作,优化算法的相关知识也都是关于“逐步迭代到损失函数最小值”的具体操作。
在讲解AutoGrad的时候,九天老师给大家详细阐述了梯度下降的细节,因此本篇章会假设你对梯度下降是熟悉的。在这里,你可以问自己以下的问题来进行自查:
- 1、梯度下降的基本流程是什么,它是怎么找到损失函数的最小值的(写出流程)?
- 2、梯度下降中是如何迭代权重 w w w的(写出公式)?
- 3、什么是梯度?什么是步长?
如果你还不能回答这些问题,那我建议你回到Lesson 6中仔细复习一下梯度下降的细节,因为上面这些问题对于之后使用PyTorch实现神经网络的优化至关重要。
一 梯度下降中的两个关键问题
我们先简单复习一下梯度下降的核心流程。观察SSE和交叉熵损失:
C E L o s s = − ∑ i = 1 m y i ( k = j ) ln σ i 其中 σ = softmax ( z ) , z = W X S S E = 1 m ∑ i = 1 m ( z i − z ^ i ) 2 其中 z = X w \begin{aligned} C E L o s s &=-\sum_{i=1}^{m} y_{i(k=j)} \ln \sigma_{i} \quad \text { 其中 } \sigma=\operatorname{softmax}(z), z=\boldsymbol{W} \boldsymbol{X} \\ S S E &=\frac{1}{m} \sum_{i=1}^{m}\left(z_{i}-\hat{z}_{i}\right)^{2} \quad \text { 其中 } z=\boldsymbol{X} \boldsymbol{w} \end{aligned} CELossSSE=−i=1∑myi(k=j)lnσi 其中 σ=softmax(z),z=WX=m1i=1∑m(zi−z^i)2 其中 z=Xw
不难发现,任意损失函数中总是包含特征张量 X X X,真实标签y或z,权重矩阵或权重向量 w w w三个元素,其中特征张量 X X X和真实标签来自于我们的数据,所以只要给定一组权重 w w w,就一定能够得出损失函数的具体数值。假设数据只有一个特征,因此只有一个权重 w w w,我们常常绘制以 w w w为横坐标, L ( w ) L(w) L(w)为纵坐标的图像: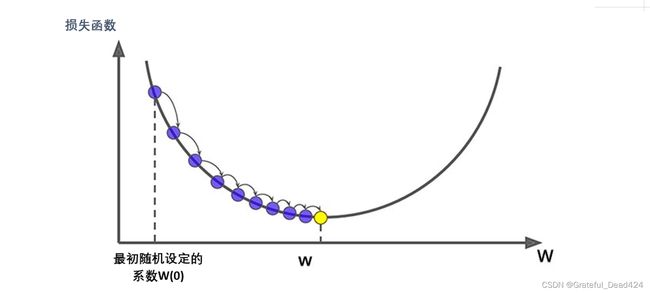
在梯度下降最开始时,我们会先随机设定初始权重 w ( 0 ) w_{(0)} w(0),对应的纵坐标 L ( w ( 0 ) ) L(w_{(0)}) L(w(0))就是初始的损失函数值,坐标点( w ( 0 ) w_{(0)} w(0), L ( w ( 0 ) ) L(w_{(0)}) L(w(0)) )就是梯度下降的起始点。
接下来,我们从起始点开始,让自变量 w w w向损失函数 L ( w ) L(w) L(w)减小最快的方向移动。以上方的图像为例,我们一眼就能看出减小损失函数最快的方向是横坐标的右侧(也就是 w w w逐渐变大的方向),但起始点是一个“盲人”,它看不到也听不到全局,每次走之前得用“拐杖”探探路,确定下方向。并且,对于复杂的图像而言(比如说下面这张图),最开始时 L ( w ) L(w) L(w)减小最快的方向(红色箭头指示的方向),不一定指向函数真正的最小值。如果一条路走到黑,最后反而可能找不到最小值点,所以”盲人“起始点每次只敢走一小段距离。每走一段距离,就要重新确认一下方向对不对,走很多步之后,才能够到达或接近损失函数的最小值。

在这个过程中,每步的方向就是当前坐标点对应的梯度向量的反方向,每步的距离就是步长 * 当前坐标点所对应的梯度向量的大小(也就是梯度向量的模长),梯度向量的性质保证了沿着其反方向、按照其大小进行移动,就能够接近损失函数的最小值。在这个过程中,存在两个关键问题:
- 1、怎么找出梯度向量的方向和大小?
- 2、怎么让坐标点按照梯度向量的反方向,移动与梯度向量大小相等的距离?
许多基于梯度下降算法的变化都是围绕这两个问题来进行。我们先来解决第一个问题。
1 找出梯度向量的方向和大小

对任意向量来说,其方向和大小都是依赖于向量元素具体的值而确定。比如向量(1,2)的方向就是从原点(0, 0)指向点(1, 2)的方向,大小就是 1 2 + 2 2 \sqrt{1^{2}+2^{2}} 12+22(向量的大小也叫模长),梯度向量的大小和方向也是如此计算。梯度向量中的具体元素就是各个自变量的偏导数,这些偏导数的具体值必须依赖于当前所在坐标点的值进行计算。所以:
- 1)梯度的大小和方向对每个坐标点而言是独一无二的。坐标点一旦变化,梯度向量的方向和大小也会变化。
- 2)每走到一个新的点,读取该点的坐标并带入梯度向量的表达式进行计算,就可以得到当前点对应的梯度向量的方向和大小。
而我们现在的坐标空间是由损失函数 L ( w ) L(w) L(w)和权重 w w w构成,只要得到一组坐标值,就可以求解当前的梯度向量。这一步骤中,最大的难点在于如何获得梯度向量的表达式——也就是损失函数对各个自变量求偏导后的表达式。
2 让坐标点移动起来(进行一次迭代)
有了大小和方向,来看第二个问题:怎么让坐标点按照梯度向量的反方向,移动与梯度向量大小相等的距离?
假设现在我们有坐标点A(10,7.5),向量 g ⃗ \vec{g} g为(5,5),大小为 5 2 5 \sqrt{2} 52。现在我们让点A向 g ⃗ \vec{g} g的反方向移动 5 2 5 \sqrt{2} 52的距离,如图所示。

这个过程非常容易。首先将向量和点都展示在同一坐标系中,然后找出向量反方向、同等长度的向量(红色箭头)。然后将反方向的向量平移,让其起点落在A点上。平移过后,反方向的向量所指向的新的点被命名为A‘,从A点到A‘点的过程,就是让A向 g ⃗ \vec{g} g的反方向移动 5 2 5 \sqrt{2} 52的距离的结果。不难发现,其实从A点移动到A’的过程,改变的是A的两个坐标值——两个坐标值分别被减去了5,就得到了A‘点。
现在,假设我们的初始点是 ( w 1 ( 0 ) , w 2 ( 0 ) ) \left(w_{1(0)}, w_{2(0)}\right) (w1(0),w2(0)),梯度向量是 ( ∂ L ∂ w 1 , ∂ L ∂ w 2 ) \left(\frac{\partial L}{\partial w_{1}}, \frac{\partial L}{\partial w_{2}}\right) (∂w1∂L,∂w2∂L),那让坐标点按照梯度向量的反方向移动的方法如下:
w 1 ( 1 ) = w 1 ( 0 ) − ∂ L ∂ w 1 w_{1(1)}=w_{1(0)}-\frac{\partial L}{\partial w_{1}} w1(1)=w1(0)−∂w1∂L w 2 ( 1 ) = w 2 ( 0 ) − ∂ L ∂ w 2 w_{2(1)}=w_{2(0)}-\frac{\partial L}{\partial w_{2}} w2(1)=w2(0)−∂w2∂L
将两个 w w w写在同一个权重向量里,用t代表走到t了第t步(即进行第t次迭代),则有
w ( t + 1 ) = w ( t ) − ∂ L ∂ w \boldsymbol{w}_{(t+1)}=\boldsymbol{w}_{(t)}-\frac{\partial L}{\partial \boldsymbol{w}} w(t+1)=w(t)−∂w∂L
为了控制每次走的距离的大小,我们将步长 η \eta η(又叫做学习率)加入公式,就可以将上面的式子改写为:
w ( t + 1 ) = w ( t ) − η ∂ L ∂ w \boldsymbol{w}_{(t+1)}=\boldsymbol{w}_{(t)}-\eta \frac{\partial L}{\partial \boldsymbol{w}} w(t+1)=w(t)−η∂w∂L
这就是我们迭代权重的迭代公式,其中偏导数的大小影响整体梯度向量的大小,偏导数前的减号影响整体梯度向量的方向。当我们将 η \eta η设置得很大,梯度下降的每一个步子就迈得很大,走得很快,当我们将步长设置较小,梯度下降就走得很慢。我们使用一个式子,就同时控制了大小和方向,不得不说大道至简,很复杂的目的在数学的世界里可以变得极其简单。
当然了,一旦迭代 w w w,我们的损失函数也会发生变化。在整个损失函数的图像上,红色箭头就是梯度向量的反方向,灰色箭头就是每个权重对应的迭代。(这个损失函数就是九天老师在AutoGrad课程中使用的SSE)。

你可以使用这一段代码,在Jupyter Notebook中实现这个3D图的绘制。注意,这段代码只在jupyter notebook中有效,jupyterlab不可用。
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits import mplot3d
import numpy as np
w1 = np.arange(-10,10,0.05)
w2 = np.arange(-10,10,0.05)
w1, w2 = np.meshgrid(w1, w2)
lossfn = (2 - w1 - w2)**2 + (4 - 3*w1 - w2)**2 #定义一个绘制三维图像的函数
#elev表示上下旋转的角度
#azim表示平行旋转的角度
def plot_3D(elev=45,azim=60,X=w1,y=w2):
fig, ax = plt.subplots(1, 1,constrained_layout=True, figsize=(8, 8))
ax = plt.subplot(projection="3d")
ax.plot_surface(w1, w2, lossfn, cmap='rainbow',alpha=0.7)
ax.view_init(elev=elev,azim=azim)
#ax.xticks([-10,-5,0,5,10])
#ax.set_xlabel("w1",fontsize=20)
#ax.set_ylabel("w2",fontsize=20)
#ax.set_zlabel("lossfn",fontsize=20)
plt.show()
from ipywidgets import interact,fixed
interact(plot_3D,elev=[0,15,30],azip=(-180,180),X=fixed(a),y=fixed(b))
plt.show()
以上就是传统梯度下降法的基础,相信现在对于梯度下降,你已经有很好的理解了。下一节,我们就从梯度下降展开,为大家介绍神经网络最为常用的优化算法之一:带动量的小批量随机梯度下降。
二、找出距离和方向:反向传播
1 反向传播的定义与价值
在梯度下降的最初,我们需要先找出坐标点对应的梯度向量。梯度向量是各个自变量求偏导后的表达式再带入坐标点计算出来的,在这一步骤中,最大的难点在于如何获得梯度向量的表达式——也就是损失函数对各个自变量求偏导后的表达式。在单层神经网络,例如逻辑回归(二分类单层神经网络)中,我们有如下计算:
其中BCEloss是二分类交叉熵损失函数。在这个计算图中,从左向右计算以此的过程就是正向传播,因此进行以此计算后,我们会获得所有节点上的张量的值(z、sigma以及loss)。根据梯度向量的定义,在这个计算过程中我们要求的是损失函数对 w w w的导数,所以求导过程需要涉及到的链路如下:
用公式来表示则为在以下式子上求解对 w w w的导数:
∂ Loss ∂ w \frac{\partial \text { Loss }}{\partial w} ∂w∂ Loss , 其中
Loss = − ∑ i = 1 m ( y i ∗ ln ( σ i ) + ( 1 − y i ) ∗ ln ( 1 − σ i ) ) = − ∑ i = 1 m ( y i ∗ ln ( 1 1 + e − X i w ) + ( 1 − y i ) ∗ ln ( 1 − 1 1 + e − X i w ) ) \begin{aligned} \text { Loss } &=-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\sigma_{i}\right)+\left(1-y_{i}\right) * \ln \left(1-\sigma_{i}\right)\right) \\ &=-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\frac{1}{1+e^{-\boldsymbol{X}_{i} \boldsymbol{w}}}\right)+\left(1-y_{i}\right) * \ln \left(1-\frac{1}{1+e^{-\boldsymbol{X}_{i} \boldsymbol{w}}}\right)\right) \end{aligned} Loss =−i=1∑m(yi∗ln(σi)+(1−yi)∗ln(1−σi))=−i=1∑m(yi∗ln(1+e−Xiw1)+(1−yi)∗ln(1−1+e−Xiw1))
可以看出,已经很复杂了。
更夸张的是,在双层的、各层激活函数都是sigmoid的二分类神经网络上,我们有如下计算流程:
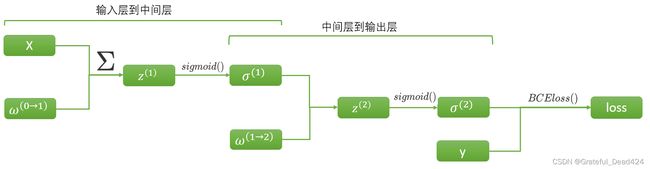 同样的,进行从左到右的正向传播之后,我们会获得所有节点上的张量。其中涉及到的求导链路如下:
同样的,进行从左到右的正向传播之后,我们会获得所有节点上的张量。其中涉及到的求导链路如下:
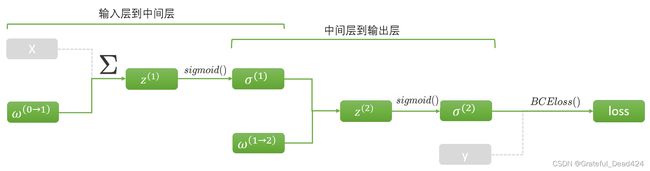
用公式来表示,对 w ( 1 → 2 ) w^{(1 \rightarrow 2)} w(1→2)我们有:
∂ L o s s ∂ w ( 1 → 2 ) \frac{\partial L o s s}{\partial w^{(1 \rightarrow 2)}} ∂w(1→2)∂Loss, 其中
Loss = − ∑ i = 1 m ( y i ∗ ln ( σ i ( 2 ) ) + ( 1 − y i ) ∗ ln ( 1 − σ i ( 2 ) ) ) = − ∑ i = 1 m ( y i ∗ ln ( 1 1 + e − σ i ( 1 ) w ( 1 → 2 ) ) + ( 1 − y i ) ∗ ln ( 1 − 1 1 + e − σ i ( 1 ) w ( 1 → 2 ) ) ) \begin{aligned} \text { Loss } &=-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\sigma_{i}^{(2)}\right)+\left(1-y_{i}\right) * \ln \left(1-\sigma_{i}^{(2)}\right)\right) \\ &=-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\frac{1}{1+e^{-\sigma_{i}^{(1)} w^{(1 \rightarrow 2)}}}\right)+\left(1-y_{i}\right) * \ln \left(1-\frac{1}{1+e^{-\sigma_{i}^{(1)} w^{(1 \rightarrow 2)}}}\right)\right) \end{aligned} Loss =−i=1∑m(yi∗ln(σi(2))+(1−yi)∗ln(1−σi(2)))=−i=1∑m(yi∗ln(1+e−σi(1)w(1→2)1)+(1−yi)∗ln(1−1+e−σi(1)w(1→2)1))
对 w ( 0 → 1 ) w^{(0 \rightarrow 1)} w(0→1)我们有:
∂ L o s s ∂ w ( 0 → 1 ) \frac{\partial L o s s}{\partial w^{(0 \rightarrow 1)}} ∂w(0→1)∂Loss, 其中
Loss = − ∑ i = 1 m ( y i ∗ ln ( σ i ( 2 ) ) + ( 1 − y i ) ∗ ln ( 1 − σ i ( 2 ) ) ) = − ∑ i = 1 m ( y i ∗ ln ( 1 1 + e − 1 1 + e − X i w ( 0 → 1 ) w ( 1 → 2 ) ) + ( 1 − y i ) ∗ ln ( 1 − 1 1 + e − 1 1 + e − X i w ( 0 → 1 ) w ( 1 → 2 ) ) ) \begin{aligned} \text { Loss } &=-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\sigma_{i}^{(2)}\right)+\left(1-y_{i}\right) * \ln \left(1-\sigma_{i}^{(2)}\right)\right) \\ &=-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\frac{1}{1+e^{-\frac{1}{1+e^{-X_{i} w^{(0 \rightarrow 1)}}} w^{(1 \rightarrow 2)}}}\right)+\left(1-y_{i}\right) * \ln \left(1-\frac{1}{\left.1+e^{-\frac{1}{1+e^{-X_{i} w^{(0 \rightarrow 1)}} w^{(1 \rightarrow 2)}}}\right)}\right)\right. \end{aligned} Loss =−i=1∑m(yi∗ln(σi(2))+(1−yi)∗ln(1−σi(2)))=−i=1∑m⎝⎜⎜⎛yi∗ln(1+e−1+e−Xiw(0→1)1w(1→2)1)+(1−yi)∗ln⎝⎜⎜⎛1−1+e−1+e−Xiw(0→1)w(1→2)1)1⎠⎟⎟⎞
对于需要对这个式子求导,大家感受如何?而这只是一个两层的二分类神经网络,对于复杂神经网络来说,所需要做得求导工作是无法想象的。求导过程的复杂是神经网络历史上的一大难题,这个难题直到1986年才真正被解决。1986年,Rumelhart、Hinton和Williams提出了反向传播算法(Backpropagation algorithm,又叫做Delta法则),利用链式法则成功实现了复杂网络求导过程的简单化。(值得一提的是,多层神经网络解决XOR异或门问题是在1985年被提出的)。接下来,我们就来看看反向传播是怎么解决复杂求导问题的。
在高等数学中,存在着如下规则:
假设有函数 u=h(z), z=f(w) , 且两个函数在各自自变量的定义域上都可导, 则有:
∂ u ∂ w = ∂ u ∂ z ∗ ∂ z ∂ w \frac{\partial u}{\partial w}=\frac{\partial u}{\partial z} * \frac{\partial z}{\partial w} ∂w∂u=∂z∂u∗∂w∂z
感性(但不严谨)地来说,当一个函数是由多个函数嵌套而成,最外层函数向最内层自变量求导的值,等于外层函数对外层自变量求导的值 * 内层函数对内层自变量求导的值。这就是链式法则。当函数之间存在复杂的嵌套关系,并且我们需要从最外层的函数向最内层的自变量求导时,链式法则可以让求导过程变得异常简单。
以双层二分类网络为例,对 w ( 1 → 2 ) w^{(1 \rightarrow 2)} w(1→2)我们本来需要求解:
∂ L o s s ∂ w ( 1 → 2 ) , 其中 L o s s = − ∑ i = 1 m ( y i ∗ ln ( σ i 2 ) + ( 1 − y i ) ∗ ln ( 1 − σ i 2 ) ) = − ∑ i = 1 m ( y i ∗ ln ( 1 1 + e − σ i 1 w ( 1 → 2 ) ) + ( 1 − y i ) ∗ ln ( 1 − 1 1 + e − σ i 1 w ( 1 → 2 ) ) ) \begin{aligned} \frac{\partial L o s s}{\partial w^{(1 \rightarrow 2)}}, \text { 其中 } & \\ L o s s &=-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\sigma_{i}^{2}\right)+\left(1-y_{i}\right) * \ln \left(1-\sigma_{i}^{2}\right)\right) \\ &=-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\frac{1}{1+e^{-\sigma_{i}^{1} \boldsymbol{w}^{(1 \rightarrow 2)}}}\right)+\left(1-y_{i}\right) * \ln \left(1-\frac{1}{1+e^{-\sigma_{i}^{1} \boldsymbol{w}^{(1 \rightarrow 2)}}}\right)\right) \end{aligned} ∂w(1→2)∂Loss, 其中 Loss=−i=1∑m(yi∗ln(σi2)+(1−yi)∗ln(1−σi2))=−i=1∑m(yi∗ln(1+e−σi1w(1→2)1)+(1−yi)∗ln(1−1+e−σi1w(1→2)1))
现在,因为Loss是一个内部嵌套了很多函数的函数,我们可以用链式法则将 ∂ L o s s ∂ w ( 1 → 2 ) \frac{\partial L o s s}{\partial w^{(1 \rightarrow 2)}} ∂w(1→2)∂Loss拆解为如下结构:
∂ L o s s ∂ w ( 1 → 2 ) = ∂ L ( σ ) ∂ σ ∗ ∂ σ ( z ) ∂ z ∗ ∂ z ( w ) ∂ w \frac{\partial L o s s}{\partial w^{(1 \rightarrow 2)}}=\frac{\partial L(\sigma)}{\partial \sigma} * \frac{\partial \sigma(z)}{\partial z} * \frac{\partial z(w)}{\partial w} ∂w(1→2)∂Loss=∂σ∂L(σ)∗∂z∂σ(z)∗∂w∂z(w)
其中,
∂ L ( σ ) ∂ σ = ∂ ( − ∑ i = 1 m ( y i ∗ ln ( σ i ) + ( 1 − y i ) ∗ ln ( 1 − σ i ) ) ) ∂ σ = ∑ i = 1 m ∂ ( − ( y i ∗ ln ( σ i ) + ( 1 − y i ) ∗ ln ( 1 − σ i ) ) ) ∂ σ \begin{aligned} \frac{\partial L(\sigma)}{\partial \sigma} &=\frac{\partial\left(-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\sigma_{i}\right)+\left(1-y_{i}\right) * \ln \left(1-\sigma_{i}\right)\right)\right)}{\partial \sigma} \\ &=\sum_{i=1}^{m} \frac{\partial\left(-\left(y_{i} * \ln \left(\sigma_{i}\right)+\left(1-y_{i}\right) * \ln \left(1-\sigma_{i}\right)\right)\right)}{\partial \sigma} \end{aligned} ∂σ∂L(σ)=∂σ∂(−∑i=1m(yi∗ln(σi)+(1−yi)∗ln(1−σi)))=i=1∑m∂σ∂(−(yi∗ln(σi)+(1−yi)∗ln(1−σi)))
求导不影响加和符号, 因此暂时不看加和符号:
= − ( y ∗ 1 σ + ( 1 − y ) ∗ 1 1 − σ ∗ ( − 1 ) ) = − ( y σ + y − 1 1 − σ ) = − ( y ( 1 − σ ) + ( y − 1 ) σ σ ( 1 − σ ) ) = − ( y − y σ + y σ − σ σ ( 1 − σ ) ) = σ − y σ ( 1 − σ ) \begin{aligned} &=-\left(y * \frac{1}{\sigma}+(1-y) * \frac{1}{1-\sigma} *(-1)\right) \\ &=-\left(\frac{y}{\sigma}+\frac{y-1}{1-\sigma}\right) \\ &=-\left(\frac{y(1-\sigma)+(y-1) \sigma}{\sigma(1-\sigma)}\right) \\ &=-\left(\frac{y-y \sigma+y \sigma-\sigma}{\sigma(1-\sigma)}\right) \\ &=\frac{\sigma-y}{\sigma(1-\sigma)} \end{aligned} =−(y∗σ1+(1−y)∗1−σ1∗(−1))=−(σy+1−σy−1)=−(σ(1−σ)y(1−σ)+(y−1)σ)=−(σ(1−σ)y−yσ+yσ−σ)=σ(1−σ)σ−y
假设我们已经进行过以此正向传播,那此时的 σ \sigma σ就是 σ ( 2 ) \sigma^{(2)} σ(2), y y y就是真实标签,我们可以很容易计算出 σ − y σ ( 1 − σ ) \frac{\sigma-y}{\sigma(1-\sigma)} σ(1−σ)σ−y的数值。
再来看剩下的两部分:
∂ σ ( z ) ∂ z = ∂ 1 1 + e − z ∂ z = ∂ ( 1 + e − z ) − 1 ∂ z = − 1 ∗ ( 1 + e − z ) − 2 ∗ e − z ∗ ( − 1 ) = e − z ( 1 + e − z ) 2 = 1 + e − z − 1 ( 1 + e − z ) 2 = 1 + e − z ( 1 + e − z ) 2 − 1 ( 1 + e − z ) 2 = 1 ( 1 + e − z ) − 1 ( 1 + e − z ) 2 = 1 ( 1 + e − z ) ( 1 − 1 ( 1 + e − z ) ) = σ ( 1 − σ ) \begin{aligned} \frac{\partial \sigma(z)}{\partial z} &=\frac{\partial \frac{1}{1+e^{-z}}}{\partial z} \\ &=\frac{\partial\left(1+e^{-z}\right)^{-1}}{\partial z} \\ &=-1 *\left(1+e^{-z}\right)^{-2} * e^{-z} *(-1) \\ &=\frac{e^{-z}}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1+e^{-z}-1}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1+e^{-z}}{\left(1+e^{-z}\right)^{2}}-\frac{1}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1}{\left(1+e^{-z}\right)}-\frac{1}{\left(1+e^{-z}\right)^{2}} \\ &=\frac{1}{\left(1+e^{-z}\right)}\left(1-\frac{1}{\left(1+e^{-z}\right)}\right) \\ &=\sigma(1-\sigma) \end{aligned} ∂z∂σ(z)=∂z∂1+e−z1=∂z∂(1+e−z)−1=−1∗(1+e−z)−2∗e−z∗(−1)=(1+e−z)2e−z=(1+e−z)21+e−z−1=(1+e−z)21+e−z−(1+e−z)21=(1+e−z)1−(1+e−z)21=(1+e−z)1(1−(1+e−z)1)=σ(1−σ)
此时的 σ \sigma σ还是 σ ( 2 ) \sigma^{(2)} σ(2)。接着:
∂ z ( w ) ∂ w = ∂ σ ( 1 ) w ∂ w = σ ( 1 ) \begin{aligned} \frac{\partial z(w)}{\partial w} &=\frac{\partial \boldsymbol{\sigma}^{(1)} \boldsymbol{w}}{\partial w} \\ &=\boldsymbol{\sigma}^{(1)} \end{aligned} ∂w∂z(w)=∂w∂σ(1)w=σ(1)
对任意一个特征权杖 w w w而言, ∂ z ( w ) ∂ w \frac{\partial z(w)}{\partial w} ∂w∂z(w)的值就等于其对应的输入值,所以如果是对于单层逻辑回归而言,这里的求导结果应该是 x x x。不过现在我们是对于双层神经网络的输出层而言,所以这个输入就是从中间层传过来的 σ 1 \sigma^{1} σ1。现在将三个导数公式整合:
∂ Loss ∂ w ( 1 → 2 ) = ∂ L ( σ ) ∂ σ ∗ ∂ σ ( z ) ∂ z ∗ ∂ z ( w ) ∂ w = σ ( 2 ) − y σ 2 ( 1 − σ ( 2 ) ) ∗ σ ( 2 ) ( 1 − σ ( 2 ) ) ∗ σ ( 1 ) = σ ( 1 ) ( σ ( 2 ) − y ) \begin{aligned} \frac{\partial \text { Loss }}{\partial w^{(1 \rightarrow 2)}} &=\frac{\partial L(\sigma)}{\partial \sigma} * \frac{\partial \sigma(z)}{\partial z} * \frac{\partial z(w)}{\partial w} \\ &=\frac{\sigma^{(2)}-y}{\sigma^{2}\left(1-\sigma^{(2)}\right)} * \sigma^{(2)}\left(1-\sigma^{(2)}\right) * \sigma^{(1)} \\ &=\sigma^{(1)}\left(\sigma^{(2)}-y\right) \end{aligned} ∂w(1→2)∂ Loss =∂σ∂L(σ)∗∂z∂σ(z)∗∂w∂z(w)=σ2(1−σ(2))σ(2)−y∗σ(2)(1−σ(2))∗σ(1)=σ(1)(σ(2)−y)
可以发现,将三个偏导数相乘之后,得到的最终的表达式其实非常简单。并且,其中所需要的数据都是我们在正向传播过程中已经计算出来的节点上的张量。同理,我们也可以得到对 w ( 0 → 1 ) w^{(0 \rightarrow 1)} w(0→1)的导数。本来我们需要求解: ∂ Loss ∂ w ( 0 → 1 ) \frac{\partial \text { Loss }}{\partial w^{(0 \rightarrow 1)}} ∂w(0→1)∂ Loss , 其中
Loss = − ∑ i = 1 m ( y i ∗ ln ( σ i ( 2 ) ) + ( 1 − y i ) ∗ ln ( 1 − σ i ( 2 ) ) ) = − ∑ i = 1 m ( y i ∗ ln ( 1 1 + e − 1 1 + e − X i w ( 0 → 1 ) w ( 1 → 2 ) ) + ( 1 − y i ) ∗ ln ( 1 − 1 1 + e − 1 1 + e − X i w ( 0 → 1 ) w ( 1 → 2 ) ) ) \begin{aligned} \text { Loss } &=-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\sigma_{i}^{(2)}\right)+\left(1-y_{i}\right) * \ln \left(1-\sigma_{i}^{(2)}\right)\right) \\ &=-\sum_{i=1}^{m}\left(y_{i} * \ln \left(\frac{1}{1+e^{-\frac{1}{1+e^{-X_{i} w^{(0 \rightarrow 1)}}} w^{(1 \rightarrow 2)}}}\right)+\left(1-y_{i}\right) * \ln \left(1-\frac{1}{\left.1+e^{-\frac{1}{1+e^{-X_{i} w^{(0 \rightarrow 1)}}} w^{(1 \rightarrow 2)}}\right)}\right)\right. \end{aligned} Loss =−i=1∑m(yi∗ln(σi(2))+(1−yi)∗ln(1−σi(2)))=−i=1∑m⎝⎜⎜⎛yi∗ln(1+e−1+e−Xiw(0→1)1w(1→2)1)+(1−yi)∗ln⎝⎜⎜⎛1−1+e−1+e−Xiw(0→1)1w(1→2))1⎠⎟⎟⎞

现在根据链式法则,就有:
∂ Loss ∂ w ( 0 → 1 ) = ∂ L ( σ ) ∂ σ ( 2 ) ∗ ∂ σ ( z ) ∂ z ( 2 ) ∗ ∂ z ( σ ) ∂ σ ( 1 ) ∗ ∂ σ ( z ) ∂ z ( 1 ) ∗ ∂ z ( w ) ∂ w ( 0 → 1 ) \frac{\partial \text { Loss }}{\partial w^{(0 \rightarrow 1)}}=\frac{\partial L(\sigma)}{\partial \sigma^{(2)}} * \frac{\partial \sigma(z)}{\partial z^{(2)}} * \frac{\partial z(\sigma)}{\partial \sigma^{(1)}} * \frac{\partial \sigma(z)}{\partial z^{(1)}} * \frac{\partial z(w)}{\partial w^{(0 \rightarrow 1)}} ∂w(0→1)∂ Loss =∂σ(2)∂L(σ)∗∂z(2)∂σ(z)∗∂σ(1)∂z(σ)∗∂z(1)∂σ(z)∗∂w(0→1)∂z(w)
其中前两项是在求解 w ( 1 → 2 ) w^{(1 \rightarrow 2)} w(1→2) 时求解过的, 而后三项的求解结果都显而易见:
= ( σ ( 2 ) − y ) ∗ ∂ z ( σ ) ∂ σ ( 1 ) ∗ ∂ σ ( z ) ∂ z ( 1 ) ∗ ∂ z ( w ) ∂ w ( 0 → 1 ) = ( σ ( 2 ) − y ) ∗ w 1 → 2 ∗ ( σ ( 1 ) ( 1 − σ ( 1 ) ) ) ∗ X \begin{aligned} &=\left(\sigma^{(2)}-y\right) * \frac{\partial z(\sigma)}{\partial \sigma^{(1)}} * \quad \frac{\partial \sigma(z)}{\partial z^{(1)}} \quad * \frac{\partial z(w)}{\partial w^{(0 \rightarrow 1)}} \\ &=\left(\sigma^{(2)}-y\right) * w^{1 \rightarrow 2} *\left(\sigma^{(1)}\left(1-\sigma^{(1)}\right)\right) * X \end{aligned} =(σ(2)−y)∗∂σ(1)∂z(σ)∗∂z(1)∂σ(z)∗∂w(0→1)∂z(w)=(σ(2)−y)∗w1→2∗(σ(1)(1−σ(1)))∗X
同样,这个表达式现在变得非常简单,并且,这个表达式中所需要的全部张量,都是我们在正向传播中已经计算出来储存好的,或者再模型建立之初就设置好的,因此在计算 w ( 0 → 1 ) w^{(0 \rightarrow 1)} w(0→1)的导数时,无需再重新计算如 σ ( 2 ) \sigma^{(2)} σ(2)这样的张量,这就为神经网络计算导数节省了时间。你是否注意到,我们是从右向左,从输出向输入,逐渐往前求解导数的表达式,并且我们所使用的节点上的张量,也是从后向前逐渐用到,这和我们正向传播的过程完全相反。这种从右到左,不断使用正向传播中的元素对梯度向量进行计算的方式,就是反向传播。
2 PyTorch实现反向传播
在梯度下降中,每走一步都需要更新梯度,所以计算量是巨大的。幸运的是,PyTorch可以帮助我们自动计算梯度,我们只需要提取梯度向量的值来进行迭代就可以了。在PyTorch中,我们有两种方式实现梯度计算。一种是使用我们之前已经学过的AutoGrad。在使用AutoGrad时,我们可以使用torch.autograd.grad()函数计算出损失函数上具体某个点/某个变量的导数,当我们需要了解具体某个点的导数值时autograd会非常关键,比如:
import torch
x = torch.tensor(1.,requires_grad = True) #requires_grad,表示允许对X进行梯度计算
y = x ** 2
torch.autograd.grad(y, x) #这里返回的是在函数y=x**2上,x=1时的导数值。
对于单层神经网络,autograd.grad会非常有效。但深层神经网络就不太适合使用grad函数了。对于深层神经网络,我们需要一次性计算大量权重对应的导数值,并且这些权重是以层为单位阻止成一个个权重的矩阵,要一个个放入autograd来进行计算有点麻烦。所以我们会直接使PyTorch提供的基于autograd的反向传播功能,lossfunction.backward()来进行计算。
注意,在实现反向传播之前,首先要完成模型的正向传播,并且要定义损失函数,因此我们会借助之前的课程中我们完成的三层神经网络的类和数据(500行,20个特征的随机数据)来进行正向传播。
我们来看具体的代码:
#导入库、数据、定义神经网络类,完成正向传播
#继承nn.Module类完成正向传播
import torch
import torch.nn as nn
from torch.nn import functional as F #确定数据
torch.manual_seed(420)
X = torch.rand((500,20),dtype=torch.float32) * 100
y = torch.randint(low=0,high=3,size=(500,),dtype=torch.float32) #定义神经网路的架构
"""
注意:这是一个三分类的神经网络,因此我们需要调用的损失函数多分类交叉熵函数CEL
CEL类已经内置了sigmoid功能,因此我们需要修改一下网络架构,删除forward函数中输出层上的sigmoid
函数,并将最终的输出修改为zhat
"""
class Model(nn.Module):
def __init__(self,in_features=10,out_features=2):
super(Model,self).__init__() #super(请查找这个类的父类,请使用找到的父类替换现在的类)
self.linear1 = nn.Linear(in_features,13,bias=True) #输入层不用写,这里是隐藏层的第一层
self.linear2 = nn.Linear(13,8,bias=True)
self.output = nn.Linear(8,out_features,bias=True)
def forward(self, x):
z1 = self.linear1(x)
sigma1 = torch.relu(z1)
z2 = self.linear2(sigma1)
sigma2 = torch.sigmoid(z2)
z3 = self.output(sigma2)
#sigma3 = F.softmax(z3,dim=1)
return z3
input_ = X.shape[1] #特征的数目
output_ = len(y.unique()) #分类的数目
#实例化神经网络类
torch.manual_seed(420)
net = Model(in_features=input_, out_features=output_) #前向传播
zhat = net.forward(X) #定义损失函数
zhat
#tensor([[-0.3347, -0.2447, -0.5918],
# [ 0.1220, -0.2206, -0.7131],
# [-0.4625, -0.0470, -1.0476],
# ...,
# [ 0.0663, -0.4350, -0.2837],
# [-0.2096, -0.4459, -0.3524],
# [-0.1692, -0.5076, -0.3820]], grad_fn=)
criterion = nn.CrossEntropyLoss()
#对打包好的CorssEnrtopyLoss而言,只需要输入zhat
loss = criterion(zhat,y.reshape(500).long())
loss
#tensor(1.1057, grad_fn=)
net.linear1.weight.grad #不会返回任何值
#反向传播,backward是任意损失函数类都可以调用的方法,对任意损失函数,backward都会求解其中全部w的梯度
loss.backward()
net.linear1.weight.grad
#tensor([[ 3.3726e-04, 8.3354e-05, 4.0867e-04, 4.3058e-05, 1.4551e-04,
# 6.5092e-05, 3.7088e-04, 2.8794e-04, 1.0495e-04, 4.7446e-05,
# 8.8153e-05, 1.6899e-04, 1.0251e-04, 3.6197e-04, 1.2129e-04,
# 7.2405e-05, 1.4479e-04, 4.9114e-06, 1.0770e-04, 9.5156e-05],
# [ 8.2042e-03, 2.1974e-02, 2.1073e-02, 1.3896e-02, 2.2161e-02,
# 1.5936e-02, 1.6537e-02, 2.0259e-02, 1.9655e-02, 1.4728e-02,
# 1.9212e-02, 2.0087e-02, 1.8295e-02, 8.4133e-03, 1.8036e-02,
# 1.9979e-02, 2.0966e-02, 2.4730e-02, 9.3876e-03, 1.7475e-02],
# [ 9.1603e-03, 2.4275e-02, 2.3446e-02, 2.0096e-02, 2.5360e-02,
# 1.7406e-02, 3.2556e-02, 2.2461e-02, 3.6793e-03, 2.7445e-02,
# 2.1181e-02, 2.7724e-02, 1.7115e-02, 1.6943e-02, 1.7249e-02,
# 3.3174e-02, 1.5115e-02, 3.0874e-02, 1.8391e-02, 2.4201e-02],
# [-2.8595e-04, 1.2968e-03, 1.3652e-03, -5.6688e-05, -1.7480e-03,
# -2.6459e-03, 3.7307e-04, -2.7976e-03, 1.7848e-03, -9.9289e-04,
# -3.3944e-04, 2.2783e-04, 1.2076e-03, -3.2906e-04, 5.4641e-04,
# -2.8959e-03, -2.7890e-03, -3.0774e-03, -3.8981e-03, -6.0863e-03],
# [ 1.5692e-03, 1.3161e-03, -9.0901e-04, -1.0158e-03, -4.9426e-03,
# 1.3061e-03, -6.8428e-03, -1.0955e-02, 4.2489e-03, -9.7841e-03,
# -3.5232e-03, -6.9716e-03, 1.0742e-02, 2.9732e-03, -2.2283e-03,
# -4.3101e-03, -1.2823e-03, -6.0040e-03, -1.5857e-03, -3.2208e-03],
# [-2.3456e-03, 3.0269e-04, -9.7571e-04, -1.7812e-03, -1.9554e-03,
# 4.7728e-04, -7.5906e-04, -9.3554e-04, -8.6828e-04, -4.9501e-04,
# -3.2291e-03, -2.6119e-03, -9.4872e-04, -1.3638e-03, -1.7115e-03,
# -9.1220e-04, -1.0843e-03, -8.5493e-04, 1.5598e-04, -2.5193e-03],
# [-1.8459e-02, -2.0008e-02, -1.3430e-02, -1.5675e-02, -1.3660e-02,
# -1.4804e-02, -8.0083e-03, -2.0027e-02, -2.9173e-02, 7.5748e-03,
# -1.8572e-02, -5.4350e-03, -3.2866e-02, -9.2504e-03, -1.8047e-02,
# -9.1732e-03, -1.6036e-02, -1.4584e-02, -8.9602e-03, 1.7229e-03],
# [ 9.5593e-04, -2.0620e-02, -2.6421e-02, -1.9139e-02, -2.5206e-02,
# -9.0115e-03, -2.5945e-02, -1.8858e-02, -3.5860e-03, -3.2187e-02,
# -1.8400e-02, -1.8522e-02, -1.1765e-02, -1.5216e-02, -8.4282e-03,
# -3.0337e-02, -1.1364e-02, -2.9159e-02, -5.1049e-03, -2.6377e-02],
# [ 3.7390e-03, -1.3553e-03, -2.2382e-03, 2.2693e-03, -1.4464e-03,
# -2.4332e-03, -3.7882e-03, 7.3998e-04, 1.2527e-02, -1.9007e-03,
# 7.8561e-03, -9.5000e-03, 9.1147e-03, -2.2882e-03, 5.5781e-03,
# -5.0263e-03, 4.8214e-03, 2.0531e-03, 4.1112e-04, -2.4565e-03],
# [ 2.4338e-03, 2.9046e-03, -1.0326e-02, -4.4876e-03, -8.1680e-05,
# -3.0232e-03, 3.2874e-03, -7.5255e-03, -1.0000e-02, 3.9967e-03,
# 6.3736e-03, -2.3521e-03, -3.5956e-03, -4.8027e-03, -2.7523e-03,
# 1.6497e-03, -1.3330e-03, 3.1406e-03, 4.9480e-03, -1.5097e-03],
# [-7.3584e-04, 9.5657e-04, 1.6132e-03, 2.9669e-03, -1.5606e-03,
# 2.1566e-03, -5.9969e-04, 1.0974e-03, 2.8536e-03, -1.5761e-03,
# -1.1973e-03, 1.4157e-03, 1.0819e-03, -1.6395e-04, 1.4259e-03,
# -1.5992e-03, 4.9925e-04, 2.4320e-03, 2.8718e-03, 7.4142e-04],
# [-1.3084e-02, -1.9413e-02, -3.0946e-02, -2.5855e-02, -2.5361e-02,
# -1.3386e-02, -1.6360e-02, -1.5787e-02, -2.4764e-02, -2.0017e-02,
# -1.5216e-02, -1.7700e-02, -1.4559e-02, -2.9177e-02, -1.7573e-02,
# -1.8530e-02, -1.0069e-02, -9.5260e-03, -1.8987e-02, -1.7839e-02],
# [ 4.8107e-04, 7.2480e-04, 9.8633e-05, 8.6471e-04, 1.9964e-03,
# 1.6202e-03, 1.1736e-03, 2.0290e-03, 3.3147e-04, 3.0171e-03,
# 1.0456e-03, 1.1400e-03, 5.0297e-04, 3.3159e-04, 1.9707e-03,
# 3.4884e-04, 8.4107e-04, 2.6777e-03, 8.6282e-04, 5.8412e-04]])
#与可以重复进行的正向传播不同,一次正向传播后,反向传播只能进行一次
#如果希望能够重复进行反向传播,可以在进行第一次反向传播的时候加上参数retain_graph
loss.backward(retain_graph=True)
loss.backward()
backward求解出的结果的结构与对应的权重矩阵的结构一模一样,因为一个权重就对应了一个偏导数。这几行代码非常简单,短到几乎不需要去记忆。咋这里,唯一需要说明的点是,在使用autograd的时候,我们强调了requires_grad的用法,但在定义打包好的类以及使用loss.backward()的时候,我们却没有给任何数据定义requires_grad=True。这是因为:
- 1、当使用nn.Module继承后的类进行正向传播时,我们的权重 w w w是自动生成的,在生成时就被自动设置为允许计算梯度(requires_grad=True),所以不需要我们自己去设置
- 2、同时,观察我们的反向传播过程:

不难发现,我们的特征张量 X X X与真实标签 y y y都不在反向传播的过程当中,但是 X X X与 y y y其实都是损失函数计算需要用的值,在计算图上,这些值都位于叶子节点上,我们在定义损失函数时,并没有告诉损失函数哪些值是自变量,哪些是常数,那backward函数是怎么判断具体求解哪个对象的梯度的呢?
其实就是靠requires_grad。首先backward值会识别叶子节点,不在叶子上的变量是不会被backward考虑的。对于全部叶子节点来说,只有属性requires_grad=True的节点,才会被计算。在设置 X X X与 y y y时,我们都没有写requires_grad参数,也就是默认让“允许求解梯度”这个选项为False,所以backward在计算的时候就只会计算关于 w w w的部分。
当然,我们也可以将 X X X和 y y y或者任何除了权重以及截距的量的requires_grad打开,一旦我们设置为True,backward就会在帮助我们计算 w w w的导数的同时,也帮我们计算以 X X X或 y y y为自变量的导数。在正常的梯度下降和反向传播过程中,我们是不需要这些导数的,因此我们一律不去管requires_grad的设置,就让它默认为False,以节约计算资源。当然,如果你的 w w w是自己设置的,千万记得一定要设置requires_grad=True。
三、移动坐标点
1 走出第一步
有了大小和方向,接下来我们就可以开始走出我们的第一步了。来看权重的迭代公式:
w ( t + 1 ) = w ( t ) − η ∂ L ( w ) ∂ w w_{(t+1)}=w_{(t)}-\eta \frac{\partial L(w)}{\partial w} w(t+1)=w(t)−η∂w∂L(w)
现在我们的偏导数部分已经计算出来了,就是我们使用backward求解出的结果。而 η \eta η学习率,或者步长,是我们在迭代开始之前就人为设置好的,一般是0.01~0.5之间的某个小数。因此现在我们已经可以无障碍地使用代码实现权重的迭代了
#在这里,我们的数据是生成的随机数,为了让大家看出效果,所以我才设置了步长为10,正常不会使用这么
大的步长
#步长、学习率的英文是learning rate,所以常常简写为lr
lr = 10
dw = net.linear1.weight.grad
w = net.linear1.weight.data
#对任意w可以有
w -= lr * dw
普通梯度下降就是在重复正向传播、计算梯度、更新权重的过程,但这个过程往往非常漫长。如大家所见,步长设置为0.001时,我们看不到w任何的变化,只有当步长设置得非常巨大,我们才能够看到一些改变,但在之前的课程中我们说过,巨大的步长可能会让我们跳过真正的最小值,所以我们无法将步长设置得很大,无论如何,梯度下降都是一个缓慢的过程。在这个基础上,我们提出了加速迭代的数个方法,其中一个很关键的方法,就是使用动量Momentum。
2 从第一步到第二步:动量法Momentum
之前我们说过,在梯度下降过程中,起始点是一个“盲人”,它看不到也听不到全局,所以我们每移动一次都要重新计算方向与距离,并且每次只能走一小步。但不只限于此,起始点不仅看不到前面的路,也无法从过去走的路中学习。
想象一下,我们被蒙上眼睛,由另一个人喊口号来给与我们方向让我们移动,假设喊口号的人一直喊:”向前,向前,向前。“因为我们看不见,在最初的三四次,我们可能都只会向前走一小步,但如果他一直让我们向前,我们就会失去耐心,转而向前走一大步,因为我们可以预测:前面很长一段路大概都是需要向前的。对梯度下降来说,也是同样的道理——如果在很长一段时间内,起始点一直向相似的方向移动,那按照步长一小步一小步地磨着向前是没有意义的,既浪费计算资源又浪费时间,此时就应该大胆地照着这个方向走一大步。相对的,如果我们很长时间都走向同一个方向,突然让我们转向,那我们转向的第一步就应该非常谨慎,走一小步。
不难发现,真正高效的方法是:在历史方向与现有方向相同的情况下,迈出大步子,在历史方向与现有方向相反的情况下,迈出小步子。那要怎么才能让起始点了解过去的方向呢?我们让上一步的梯度向量与现在这一点的梯度向量以加权的方式求和,求解出受到上一步大小和方向影响的真实下降方向,再让坐标点向真实下降方向移动。在坐标轴上,可以表示为:

其中,对上一步的梯度向量加上的权重被称为动量参数(也叫做衰减力度,通常使用 γ \gamma γ进行表示),对这一点的梯度向量加上的权重就是步长(依然表示为 η \eta η),真实移动的向量为 v v v,被称为”动量“(Momentum)。将上述过程使用公式表示,则有:
v ( t ) = γ v ( t − 1 ) − η L ∂ w w ( t + 1 ) = w ( t ) + v ( t ) \begin{aligned} v_{(t)} &=\gamma v_{(t-1)}-\eta \frac{L}{\partial \boldsymbol{w}} \\ \boldsymbol{w}_{(t+1)} &=\boldsymbol{w}_{(t)}+v_{(t)} \end{aligned} v(t)w(t+1)=γv(t−1)−η∂wL=w(t)+v(t)
在第一步中,没有历史梯度方向,因此第一步的真实方向就是起始点梯度的反方向, v 0 = 0 v_{0}=0 v0=0。其中 v ( t − 1 ) v_{(t-1)} v(t−1)代表了之前所有步骤所累积的动量和。在这种情况下,梯度下降的方向有了==“惯性”==,受到历史累计动量的影响,当新坐标点的梯度反方向与历史累计动量的方向一致时,历史累计动量会加大实际方向的步子,相反,当新坐标点的梯度反方向与历史累计动量的方向不一致时,历史累计动量会减小实际方向的步子。
我们可以很容易地在PyTorch中实现动量法:
#恢复小步长
lr = 0.1
gamma = 0.9
dw = net.linear1.weight.grad
w = net.linear1.weight.data
v = torch.zeros(dw.shape[0],dw.shape[1])
#v要能够跟dw相减,因此必须和dw保持相同的结构,初始v为0,但后续v会越来越大
#==========分割cell,不然重复运行的时候w会每次都被覆盖掉=============
#对任意w可以有
v = gamma * v - lr * dw
w += v
w
#不难发现,当加入gamma之后,即便是较小的步长,也可以让w发生变化
3 torch.optim实现带动量的梯度下降
在PyTorch库的架构中,拥有专门实现优化算法的模块torch.optim。我们在之前的课程中所说的迭代流程,都可以通过torch.optim模块来简单地实现。

接下来,我们就基于之前定义的类Model来实现梯度下降的一轮迭代:
#导入库
import torch
import torch.nn as nn
import torch.optim as optim
from torch.nn import functional as F #确定数据、确定优先需要设置的值
lr = 0.1
gamma = 0.9
torch.manual_seed(420)
X = torch.rand((500,20),dtype=torch.float32) * 100
y = torch.randint(low=0,high=3,size=(500,1),dtype=torch.float32)
input_ = X.shape[1] #特征的数目
output_ = len(y.unique()) #分类的数目
#定义神经网路的架构
class Model(nn.Module):
def __init__(self,in_features=10,out_features=2):
super(Model,self).__init__() #super(请查找这个类的父类,请使用找到的父类替换现在的类)
self.linear1 = nn.Linear(in_features,13,bias=True) #输入层不用写,这里是隐藏层的第一层
self.linear2 = nn.Linear(13,8,bias=True)
self.output = nn.Linear(8,out_features,bias=True)
def forward(self, x):
z1 = self.linear1(x)
sigma1 = torch.relu(z1)
z2 = self.linear2(sigma1)
sigma2 = torch.sigmoid(z2)
z3 = self.output(sigma2)
#sigma3 = F.softmax(z3,dim=1)
return z3
#实例化神经网络,调用优化算法需要的参数
torch.manual_seed(420)
net = Model(in_features=input_, out_features=output_)
[*net.parameters()]
# [Parameter containing:
# tensor([[ 1.3656e-01, -1.3459e-01, 2.1281e-01, -1.7763e-01, -6.8218e-02,
# -1.5410e-01, 1.7245e-01, 8.3885e-02, -1.1153e-01, -1.7294e-01,
# -1.2947e-01, -4.3138e-02, -1.1413e-01, 1.6295e-01, -9.4082e-02,
# -1.4629e-01, -6.8982e-02, -2.1836e-01, -1.0859e-01, -1.2199e-01],
# [ 4.8127e-02, 1.8186e-01, 2.4149e-02, -1.3032e-01, 9.2056e-02,
# -9.5202e-02, -1.0584e-01, -4.2852e-02, -1.1669e-01, 2.4581e-02,
# 1.8152e-01, 3.0500e-02, 1.3506e-01, -1.9425e-01, -1.7591e-01,
# -2.9751e-02, 2.0485e-04, 1.3957e-01, -1.9666e-01, 9.3293e-02],
# [-1.9192e-01, 3.6070e-02, 1.4778e-01, 3.0845e-02, 7.1393e-02,
# 1.4217e-01, 2.2122e-01, -1.4032e-01, 7.3255e-02, 1.8409e-01,
# 1.2716e-01, -2.0253e-01, -1.5509e-01, -2.1899e-01, 9.8980e-02,
# 2.2123e-01, -2.1659e-01, 1.7880e-01, -2.0922e-01, -2.7275e-02],
# [ 1.8144e-01, -3.5166e-02, 2.4801e-02, 1.6299e-01, -1.8755e-01,
# 5.6587e-02, -1.0911e-01, 2.0523e-01, -1.9378e-01, 1.6899e-02,
# 1.3966e-01, -1.3137e-01, -1.3201e-01, 7.6554e-02, -1.7558e-01,
# 1.3096e-01, 2.7182e-02, -2.2010e-01, 7.6883e-02, -1.8731e-01],
# [ 2.7419e-02, 1.3699e-01, -3.8687e-02, 8.3463e-02, -1.5634e-02,
# -1.6781e-01, -2.1426e-01, 1.8463e-01, 8.3891e-02, 5.9950e-02,
# -2.0538e-01, -2.7832e-02, 4.7442e-02, -1.9782e-01, -1.7842e-01,
# 1.1362e-01, 1.4101e-01, -1.3794e-01, 1.1704e-01, -3.4108e-02],
# [ 3.8388e-02, -1.7268e-01, -1.0235e-01, -1.2634e-01, -1.1883e-01,
# -1.3463e-01, -1.7610e-01, 3.6543e-02, -1.7834e-01, -1.6471e-01,
# 2.0834e-01, 1.8400e-01, -8.8723e-02, -7.5378e-02, 1.7877e-01,
# -5.7259e-02, -2.4522e-02, -1.1822e-02, -1.8196e-01, 1.9812e-01],
# [-2.2011e-02, 2.1847e-01, 1.8410e-01, 9.7177e-02, -5.0634e-03,
# -2.4731e-03, 5.1408e-03, -2.1733e-01, -5.3375e-02, -1.0346e-01,
# -1.3303e-02, 2.7354e-02, -1.7523e-01, 1.6994e-01, 1.8259e-01,
# 1.3907e-01, 1.0041e-01, 3.5377e-02, -1.6114e-01, 9.0056e-02],
# [ 7.9232e-02, 2.1614e-01, -2.1087e-01, 1.9407e-01, 1.7559e-01,
# 4.1470e-02, 7.4482e-02, 2.6737e-02, -1.7872e-02, 4.5040e-02,
# 1.2947e-01, 2.5483e-02, -2.0320e-02, -7.3942e-03, -1.7221e-01,
# -1.0705e-01, 1.8203e-01, 1.3179e-02, 2.3468e-02, -1.9567e-01],
# [ 1.6338e-01, 8.0209e-03, -2.9885e-02, -2.1884e-01, 1.3471e-01,
# -2.8901e-02, -1.8757e-01, 8.9256e-03, 2.0940e-01, 9.0927e-02,
# -8.2969e-02, -9.0893e-03, 1.0047e-01, -1.6897e-02, -1.3736e-01,
# 1.6801e-01, -1.9342e-01, -3.4822e-02, 1.0057e-01, 2.2273e-02],
# [ 1.4611e-01, 1.4414e-01, -2.3093e-02, 8.1946e-02, 5.9792e-03,
# 6.7672e-02, 1.5254e-01, 1.6742e-01, -1.6896e-01, 1.1571e-01,
# -1.8538e-01, 2.3316e-02, -1.6147e-01, 1.0230e-01, -1.7314e-01,
# -1.8906e-01, -2.0286e-01, -2.1210e-02, -2.1799e-02, -3.7921e-02],
# [ 1.9375e-01, 5.3921e-02, -1.4900e-01, 1.6709e-01, -1.6652e-01,
# 6.2363e-02, -4.1574e-02, -2.0565e-01, -1.3649e-01, -2.0600e-01,
# -1.9032e-01, -8.8942e-02, -7.8061e-02, 1.6323e-01, -1.3174e-01,
# 5.8638e-02, 2.1117e-01, 1.6707e-01, -5.9492e-02, -2.0973e-01],
# [-2.5644e-02, -1.0818e-02, -3.3051e-02, 3.7071e-02, -1.0809e-01,
# 2.0642e-01, 1.2396e-01, -2.1523e-01, 1.2172e-01, -1.4323e-01,
# 1.1334e-01, 4.6931e-02, 8.4553e-02, 2.0530e-01, -1.1833e-01,
# 1.9287e-01, -2.8398e-02, 7.1443e-03, -2.1055e-01, 1.0805e-01],
# [-1.2258e-01, -6.8325e-02, -2.1929e-01, -1.4939e-01, 1.9226e-01,
# -6.2922e-02, -7.6377e-02, 2.1955e-01, -4.5838e-02, 9.8011e-03,
# -2.9400e-03, -9.5241e-02, -7.9775e-02, -1.8708e-01, 1.7828e-01,
# -1.7552e-01, -1.0328e-01, -1.9697e-02, -1.7449e-01, 2.0408e-02]],
# requires_grad=True),
# Parameter containing:
# tensor([ 1.3508e-01, 1.5439e-01, -1.9350e-01, -6.8777e-02, 1.3787e-01,
# -1.8474e-01, 1.2763e-01, 1.8031e-01, 9.5152e-02, -1.2660e-01,
# 1.4317e-01, -1.4945e-01, 3.4258e-05], requires_grad=True),
# Parameter containing:
# tensor([[-0.0854, 0.0825, 0.1020, -0.0941, 0.2054, 0.2645, -0.2198, -0.0169,
# 0.0017, -0.2714, -0.1154, 0.0410, -0.0668],
# [-0.2668, 0.1752, -0.2743, 0.1611, -0.1190, 0.0476, 0.0036, 0.2185,
# -0.1021, 0.2397, 0.1055, -0.0704, -0.1420],
# [ 0.2249, -0.2563, -0.2121, -0.0678, 0.1129, 0.0035, 0.0988, 0.2494,
# 0.1891, -0.0448, 0.1583, 0.0126, 0.2220],
# [-0.2095, -0.1938, -0.0562, -0.2183, -0.2483, 0.2078, 0.2142, 0.0754,
# -0.2532, 0.1142, 0.0657, -0.0808, 0.2725],
# [ 0.2063, 0.0870, -0.2641, 0.2648, 0.1443, -0.2759, 0.0101, 0.1611,
# 0.2489, -0.1175, 0.0537, -0.0365, 0.2095],
# [ 0.2333, -0.0148, -0.2440, 0.0268, 0.1815, 0.2528, -0.2730, 0.2145,
# 0.0205, -0.2279, 0.0727, -0.2309, -0.1754],
# [-0.1644, -0.0508, 0.0548, 0.0702, -0.1867, -0.0818, 0.2041, -0.0269,
# -0.1098, -0.0464, 0.1511, 0.0050, -0.1364],
# [ 0.2180, -0.0104, 0.1469, -0.0562, -0.2288, -0.0920, 0.1706, -0.1874,
# -0.1059, -0.0818, -0.2628, -0.2723, 0.1970]], requires_grad=True),
# Parameter containing:
# tensor([ 0.0900, -0.0597, 0.0268, -0.0173, 0.0065, 0.0228, -0.1408, 0.1188],
# requires_grad=True),
# Parameter containing:
# tensor([[ 0.1259, 0.1116, -0.0097, -0.1100, 0.0427, 0.3335, -0.2140, -0.2908],
# [-0.0166, 0.0617, -0.2413, 0.0719, -0.0847, -0.0331, -0.1862, 0.1859],
# [-0.1704, 0.1227, 0.3419, 0.0164, -0.2700, -0.0598, -0.2827, -0.3440]],
# requires_grad=True),
# Parameter containing:
# tensor([-0.0156, -0.0730, -0.2637], requires_grad=True)]
#定义损失函数
criterion = nn.CrossEntropyLoss()
#定义优化算法
opt = optim.SGD(net.parameters() #要优化的参数是哪些?
, lr=lr #学习率
, momentum = gamma) #动量参数
接下来开始进行一轮梯度下降:
zhat = net.forward(X) #向前传播
loss = criterion(zhat,y.reshape(500).long()) #损失函数值
loss.backward() #反向传播
opt.step() #更新权重w,从这一瞬间开始,坐标点就发生了变化,所有的梯度必须重新计算
opt.zero_grad() #清除原来储存好的,基于上一个坐标点计算的梯度,为下一次计算梯度腾出空间
print(loss)
print(net.linear1.weight.data[0][:10])
#tensor(1.0954, grad_fn=)
#tensor([ 0.1364, -0.1346, 0.2126, -0.1776, -0.0683, -0.1541, 0.1723, 0.0837,-0.1116, -0.1730, -0.1295, -0.0432, -0.1142, 0.1628, -0.0941, -0.1463,-0.0691, -0.2184, -0.1086, -0.1220])
多运行几次试试看,我们的损失函数与权重都在变化。这一段代码就是实现了梯度下降中的一步,多次运行就是实现了梯度下降本身。
四、开始迭代:batch_size与epoches
1 为什么要有小批量?
在实现一轮梯度下降之后,只要在梯度下降的代码外面加上一层循环,就可以顺利实现迭代多次的梯度下降了。但在那之前,还有另外一个问题。为了提升梯度下降的速度,我们在使用了动量法,同时,我们也要在使用的数据上下功夫。
在深度学习的世界中,神经网络的训练对象往往是图像、文字、语音、视频等非结构化数据,这些数据的特点之一就是特征张量一般都是大量高维的数据。比如在深度学习教材中总是被用来做例子的入门级数据MNIST,其训练集的结构为(60000,784)。对比机器学习中的入门级数据鸢尾花(结构为(150,4)),两者完全不在一个量级上。在深度学习中,如果梯度下降的每次迭代都使用全部数据,将会非常耗费计算资源,且样本量越大,计算开销越高。虽然PyTorch被设计成天生能够处理巨量数据,但我们还是需要在数据量这一点上下功夫。这一节,我们开始介绍小批量随机梯度下降(mini-batch stochastic gradient descent,简写为mini-batch SGD)。
小批量随机梯度下降是深度学习入门级的优化算法(梯度下降是入门级之下的),其求解与迭代流程与传统梯度下降(GD)基本一致,不过二者在迭代权重时使用的数据这一点上存在巨大的不同。传统梯度下降在每次进行权重迭代(即循环)时都使用全部数据,每次迭代所使用的数据也都一致。而minibatch SGD是每次迭代前都会从整体采样一批固定数目的样本组成批次(batch)B,并用B中的样本进行梯度计算,以减少样本量。
为什么会选择mini-batch SGD作为神经网络的入门级优化算法呢?有两个比较主流的原因。第一个是,比起传统梯度下降,mini-batch SGD更可能找到全局最小值。
梯度下降是通过最小化损失函数来找对应参数向量的优化算法。对于任意损失函数 L ( w ) L(w) L(w)而言,如果 L ( w ) L(w) L(w)在其他点上的值比在 w ∗ w^{*} w∗上的值更小,那么 L ( w ∗ ) L\left(w^{*}\right) L(w∗)很可能就是一个局部最小值(local minimum)。如果 L ( w ) L(w) L(w)在 w ∗ w^{*} w∗上的值是目标函数在整个定义域上的最小值,那么 L ( w ∗ ) L\left(w^{*}\right) L(w∗)就是全局最小值(global minimum)。一个最容易理解的描述是,如果把地球海拔看作是一个函数,那世界上的许多海沟和盆地都是当地海拔最低的地区,他们就是一个个局部最小值,相对的,世界上最深的马里亚纳海沟就是海拔这个函数上的全局最小值,因为全世界没有比它更深的海底了。

尽可能找到全局最优一直都是优化算法的目标。为什么说mini-batch SGD更容易找到全局最优呢?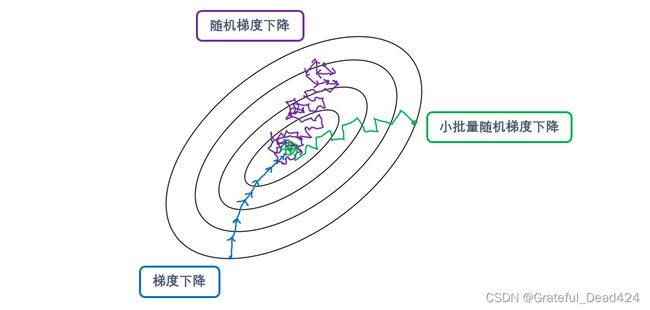
传统梯度下降是每次迭代时都使用全部数据的梯度下降,所以每次使用的数据是一致的,因此梯度向量的方向和大小都只受到权重 w w w的影响,所以梯度方向的变化相对较小,很多时候看起来梯度甚至是指向一个方向(如上图所示)。这样带来的优势是可以使用较大的步长,快速迭代直到找到最小值。但是缺点也很明显,由于梯度方向不容易发生巨大变化,所以一旦在迭代过程中落入局部最优的范围,传统梯度下降就很难跳出局部最优,再去寻找全局最优解了。
而mini-batch SGD在每次迭代前都会随机抽取一批数据,所以每次迭代时带入梯度向量表达式的数据是不同的,梯度的方向同时受到系数 w , b w,b w,b和带入的训练数据的影响,因此每次迭代时梯度向量的方向都会发生较大变化。并且,当抽样的数据量越小,本次迭代中使用的样本数据与上一次迭代中使用的样本数据之间的差异就可能越大,这也导致本次迭代中梯度的方向与上一次迭代中梯度的方向有巨大差异。所以对于mini-batch SGD而言,它的梯度下降路线看起来往往是曲折的折线(如上图所示)。
极端情况下,当我们每次随机选取的批量中只有一个样本时,梯度下降的迭代轨迹就会变得异常不稳定(如上图所示)。我们称这样的梯度下降为随机梯度下降(stochastic gradient descent,SGD)。
mini-batch SGD的优势是算法不会轻易陷入局部最优,由于每次梯度向量的方向都会发生巨大变化,因此一旦有机会,算法就能够跳出局部最优,走向全局最优(当然也有可能是跳出一个局部最优,走向另一个局部最优)。不过缺点是,需要的迭代次数变得不明。如果最开始就在全局最优的范围内,那可能只需要非常少的迭代次数就收敛,但是如果最开始落入了局部最优的范围,或全局最优与局部最优的差异很小,那可能需要花很长的时间、经过很多次迭代才能够收敛,毕竟不断改变的方向会让迭代的路线变得曲折。
从整体来看,为了mini-batch SGD这“不会轻易被局部最优困住”的优点,我们在神经网络中使用它作为优化算法(或优化算法的基础)。当然,还有另一个流传更广、更为认知的理由支持我们使用minibatch SGD:mini-batch SGD可以提升神经网络的计算效率,让神经网络计算更快。
为了解决计算开销大的问题,我们要使用mini-batch SGD。考虑到可以从全部数据中选出一部分作为全部数据的“近似估计",然后用选出的这一部分数据来进行迭代,每次迭代需要计算的数据量就会更少,计算消耗也会更少,因此神经网络的速度会提升。当然了,这并不是说使用1001个样本进行迭代一定比使用1000个样本进行迭代速度要慢,而是指每次迭代中计算上十万级别的数据,会比迭代中只计算一千个数据慢得多。
2 batch_size与epoches
在mini-batch SGD中,我们选择的批量batch含有的样本数被称为batch_size,批量尺寸,这个尺寸一定是小于数据量的某个正整数值。每次迭代之前,我们需要从数据集中抽取batch_size个数据用于训练。
在普通梯度下降中,因为没有抽样,所以每次迭代就会将所有数据都使用一次,迭代了t次时,算法就将数据学习了t次。可以想象,对同样的数据,算法学习得越多,也有应当对数据的状况理解得越深,也就学得越好。然而,并不是对一个数据学习越多越好,毕竟学习得越多,训练时间就越长,同时,我们能够收集到的数据只是“样本”,并不能够代表真实世界的客观情况。例如,我们从几万张猫与狗的照片中学到的内容,并不一定就能适用于全世界所有的猫和狗。如果我们的照片中猫咪都是有毛的,那神经网络对数据学习的程度越深,它就越有可能认不出无毛猫。因此,虽然我们希望算法对数据了解很深,但我们也希望算法不要变成”书呆子“,要保留一些灵活性(保留一些泛化能力)。关于这一点,我们之后会详细展开来说明,但大家现在需要知道的是,算法对同样的数据进行学习的次数并不是越多越好。
在mini-batch SGD中,因为每次迭代时都只使用了一小部分数据,所以它迭代的次数并不能代表全体数据一共被学习了多少次。所以我们需要另一个重要概念:epoch,读音/ˈepək/,来定义全体数据一共被学习了多少次。

假设一个数据集总共有m 个样本,我们选择的batch_size是 N B N_{B} NB,即每次迭代时都使用 N B N_{B} NB个样本,则一个epoch所需的迭代次数的计算公式如下:
完成一个 epoch所需要的迭代次数 n = m N B \text { 完成一个 epoch所需要的迭代次数 } n=\frac{m}{N_{B}} 完成一个 epoch所需要的迭代次数 n=NBm
在深度学习中,我们常常定义num_epoches作为梯度下降的最外层循环,batch_size作为内层循环。有时候,我们希望数据被多学习几次,来增加模型对数据的理解。有时候,我们会控制模型对数据的训练。总之,我们会使用epoch和batch_size来控制训练的节奏。接下来,我们就用代码来实现一下。
3 TensorDataset与DataLoader

要使用小批量随机梯度下降,我们就需要对数据进行采样、分割等操作。在PyTorch中,操作数据所需要使用的模块是torch.utils,其中utils.data类下面有大量用来执行数据预处理的工具。在MBSGD中,我们需要将数据划分为许多组特征张量+对应标签的形式,因此最开始我们要将数据的特征张量与标签打包成一个对象。之前我们提到过,深度学习中的特征张量维度很少是二维,因此其特征张量与标签几乎总是分开的,不像机器学习中标签常常出现在特征矩阵的最后一列或第一列。在我们之前的例子中,我们是单独生成了标签与特征张量,所以也需要合并,如果你的数据本来就是特征张量与标签在同一个张量中,那你可以跳过这一步。
合并张量与标签,我们所使用的类是utils.data.TensorDataset,这个功能类似于python中的zip,可以将最外面的维度一致的tensor进行打包,也就是将第一个维度一致的tensor进行打包。我们来看一下:
import torch
from torch.utils.data import TensorDataset
a = torch.randn(500,2,3)
b = torch.randn(500,3,4,5)
c = torch.randn(500,1)
TensorDataset(a,b,c)[0] #试试看合并a与c,我们一般合并特征张量与标签,就是这样合并的
#(tensor([[-0.5498, -0.6580, 0.9617],
# [-0.1631, 1.2819, 0.2725]]),
# tensor([[[ 0.3641, 1.1461, 1.3315, -0.6803, -0.1573],
# [-0.3813, 0.0569, 1.4741, -0.2237, 0.4374],
# [ 0.4338, 0.7315, -0.2749, 0.0160, -0.2451],
# [-0.5867, -0.5889, 1.8905, -0.7718, -1.7899]],
#
# [[-0.4048, 0.7898, 0.3773, 0.7166, 0.0490],
# [-0.9121, -0.0489, -0.8179, -1.8548, -0.3418],
# [ 0.0873, 0.3071, -0.9272, 1.4546, -0.8360],
# [ 1.2235, 1.2197, -0.5222, 0.2297, -0.8180]],
#
# [[ 0.4578, -2.0396, -0.1589, -0.3033, -0.6102],
# [ 1.1299, 0.8919, -0.5627, 0.4364, -0.2321],
# [ 0.1634, 1.4667, -0.7651, -0.6503, 0.0228],
# [ 0.8123, 0.9057, 1.3573, -0.3826, 0.2580]]]),
# tensor([-0.4762]))
TensorDataset(a,c)[0] #如果合并的tensor的最外层的维度不相等
#(tensor([[ 0.1243, 0.4218, -0.0191],
# [-1.1607, -0.4629, 0.7467]]),
# tensor([0.4655]))
c = torch.randn(300,1)
TensorDataset(a,c)[0]
'''AssertionError: Size mismatch between tensors'''
当我们将数据打包成一个对象之后,我们需要使用划分小批量的功能DataLoader。DataLoader是处理训练前专用的功能,它可以接受任意形式的数组、张量作为输入,并把他们一次性转换为神经网络可以接入的tensor。
data = TensorDataset(b,c)
[*data]
#[(tensor([[[ 0.5833, -0.6301, 0.3208, -0.8566, -0.4091],
# [-0.6623, -0.9799, 0.8345, 1.2860, -0.5565],
# [ 0.5795, 0.2006, 1.8063, 1.7884, -1.0874],
# [-0.7936, -0.7186, -0.9368, 1.1768, 1.5112]],
#
# [[-2.5633, -0.9876, 0.6476, 0.3364, 1.5749],
# [ 0.5582, 0.1204, 0.5306, -0.2363, 0.8692],
# [-0.4962, -1.3511, 2.1306, 0.4944, -0.4440],
# [-0.6721, 0.0417, -0.3516, 0.5302, 3.1064]],
#
# [[-0.5838, 0.7075, 0.1300, -0.3853, 0.7238],
# [ 0.9808, 1.0655, -0.7117, 0.7009, 0.1192],
# [-0.6129, 1.2972, 0.9845, -0.1717, -0.1597],
# [-0.0601, -0.1556, 1.1944, -1.0640, -0.0652]]]),
# tensor([1.2723])),
from torch.utils.data import DataLoader
DataLoader(data)
[*DataLoader(data)]
#[[tensor([[[[ 0.5833, -0.6301, 0.3208, -0.8566, -0.4091],
# [-0.6623, -0.9799, 0.8345, 1.2860, -0.5565],
# [ 0.5795, 0.2006, 1.8063, 1.7884, -1.0874],
# [-0.7936, -0.7186, -0.9368, 1.1768, 1.5112]],
#
# [[-2.5633, -0.9876, 0.6476, 0.3364, 1.5749],
# [ 0.5582, 0.1204, 0.5306, -0.2363, 0.8692],
# [-0.4962, -1.3511, 2.1306, 0.4944, -0.4440],
# [-0.6721, 0.0417, -0.3516, 0.5302, 3.1064]],
#
# [[-0.5838, 0.7075, 0.1300, -0.3853, 0.7238],
# [ 0.9808, 1.0655, -0.7117, 0.7009, 0.1192],
# [-0.6129, 1.2972, 0.9845, -0.1717, -0.1597],
# [-0.0601, -0.1556, 1.1944, -1.0640, -0.0652]]]]),
# tensor([[1.2723]])],
a = DataLoader(data,
batch_size = 120,
shuffle = True, #划分小批量之前请随机打乱我们的数据
drop_last = True,
#如果设置为True,当最后一个batch样本不够组成一个batch_size时,就会抛弃最后一个batch
#设置为False,则会保留一个较小的batch
#默认为False
)
for i in a:
print(i[0].shape)
#torch.Size([120, 3, 4, 5])
#torch.Size([120, 3, 4, 5])
#torch.Size([120, 3, 4, 5])
#torch.Size([120, 3, 4, 5])
len(a)
#4
len(a.dataset)
#500
a.dataset[0]
#(tensor([[[ 0.4045, -1.7863, 0.7452, -0.7284, -0.7738],
# [-0.0565, -0.3154, 1.1734, -0.4074, 0.2712],
# [-0.5382, 0.4380, -0.1928, -0.5690, 1.0315],
# [ 0.1129, -0.7532, 0.7754, 0.8832, -1.0667]],
#
# [[ 0.6852, -0.1069, -1.1597, 0.4301, -0.5539],
# [-1.7320, 1.3976, 0.5463, 1.7481, 0.2906],
# [-0.2126, -0.0062, -0.5251, 0.5974, -0.0966],
# [ 0.0174, 0.2435, -1.1453, -1.1682, -1.4226]],
#
# [[-0.6717, 0.7388, 0.1465, 1.0691, -0.4704],
# [ 1.3731, -0.4703, 1.2853, -0.8179, -0.1304],
# [-2.0745, 0.1218, 0.5867, -0.6374, -0.5945],
# [ 0.9434, -0.9394, 1.2917, -1.4723, -0.4411]]]),
# tensor([0.4996]))
a.batch_size
#120
对于小批量随机梯度下降而言,我们一般这样使用TensorDataset与DataLoader:
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
torch.manual_seed(420)
X = torch.rand((50000,20),dtype=torch.float32) * 100 #要进行迭代了,增加样本数量
y = torch.randint(low=0,high=3,size=(50000,1),dtype=torch.float32)
epochs = 4
bs = 4000
data = TensorDataset(X,y)
batchdata = DataLoader(data, batch_size=bs, shuffle = True)
len(batchdata) #查看具体被分了多少个batch
#13
#可以使用.datasets查看数据集相关的属性
len(batchdata.dataset) #总共有多少数据
#50000
batchdata.dataset[0] #查看其中一个样本
batchdata.dataset[0][0]#一个样本的特征张量
batchdata.dataset[0][1]#一个样本的标签
#属性batch_size,查看现在的batch_size是多少
batchdata.batch_size
#4000
#我们在迭代的时候,常常这样使用:
for batch_idx, (x,y) in enumerate(batchdata):
#sigma = net(x)
#loss = lossfn(sigma, y)
#loss.backward()
#opt.step()
#opt.zero_grad()
print(x.shape)
print(y.shape)
print(x,y)
if batch_idx == 2:
break #为了演示用,所以打断,在正常的循环里是不会打断的
#torch.Size([4000, 20])
#torch.Size([4000, 1])
#tensor([[61.9796, 54.1928, 40.4692, ..., 49.0970, 12.0571, 58.9000],
# [94.0418, 34.8577, 43.7495, ..., 80.7607, 15.6174, 42.9901],
# [27.2522, 34.0642, 1.2531, ..., 52.7913, 25.7024, 99.3192],
# ...,
# [18.1655, 9.5231, 21.3866, ..., 24.1631, 31.9831, 47.2580],
# [78.4650, 54.8282, 53.7001, ..., 86.6494, 77.6398, 91.4095],
# [75.7589, 90.4107, 27.1545, ..., 52.8371, 59.6953, 42.9755]]) tensor([[0.],
# [2.],
# [1.],
# ...,
# [0.],
# [0.],
# [1.]])
#torch.Size([4000, 20])
#torch.Size([4000, 1])
#tensor([[71.7346, 39.6868, 90.4613, ..., 54.5391, 90.9168, 16.1636],
# [61.5704, 31.9656, 26.1343, ..., 97.6185, 36.3351, 51.7871],
# [ 0.8974, 16.6530, 44.1519, ..., 60.8294, 67.9232, 85.8847],
...,
# [66.5742, 51.5837, 35.1713, ..., 32.0447, 35.4181, 49.6892],
# [75.4937, 31.4821, 46.6257, ..., 67.4422, 47.9548, 99.2506],
# [33.8725, 18.6879, 81.6916, ..., 86.6003, 37.4381, 74.6932]]) tensor([[2.],
# [1.],
# [1.],
# ...,
# [2.],
# [2.],
# [2.]])
#torch.Size([4000, 20])
#torch.Size([4000, 1])
#tensor([[64.1965, 70.5319, 70.9819, ..., 38.1955, 11.5732, 55.2129],
# [84.1224, 68.6861, 54.3906, ..., 6.9531, 99.0248, 94.4059],
# [ 8.4163, 90.3594, 80.9922, ..., 34.7041, 30.5861, 60.1388],
# ...,
# [12.2004, 91.2041, 18.1603, ..., 7.9548, 8.3422, 49.1473],
# [98.8518, 87.1700, 10.2839, ..., 92.7891, 65.7769, 65.2986],
# [73.2602, 61.5012, 53.2826, ..., 72.9232, 57.9865, 32.1918]]) tensor([[0.],
# [1.],
# [1.],
# ...,
# [1.],
# [1.],
# [2.]])
除了自己生成数据之外,我们还可以将外部导入的数据放到TensorDataset与DataLoader里来使用:
#导入sklearn中的数据
from sklearn.datasets import load_breast_cancer as LBC
data = LBC()
X = torch.tensor(data.data,dtype=torch.float32)
y = torch.tensor(data.target,dtype=torch.float32)
data = TensorDataset(X,y)
batchdata = DataLoader(data, batch_size=5, shuffle = True)
for x, y in batchdata:
print(x)
#从pandas导入数据
import pandas as pd
import numpy as np
data = pd.read_csv(r"C:\Pythonwork\DEEP LEARNING\WEEK 3\Datasets\creditcard.csv")
data.shape
data.head()
X = torch.tensor(np.array(data.iloc[:,:-1]),dtype=torch.float32)
y = torch.tensor(np.array(data.iloc[:,-1]),dtype=torch.float32)
data = TensorDataset(X,y)
batchdata = DataLoader(data, batch_size=1000,shuffle=True)
for x,y in batchdata:
print(x)
现在已经完成了对数据最基本的处理(让它能够被输入神经网络),现在让我们来从0实现神经网络的学习流程吧。
五、在MINST-FASHION上实现神经网络的学习流程
本节课我们讲解了神经网络使用小批量随机梯度下降进行迭代的流程,现在我们要整合本节课中所有的代码实现一个完整的训练流程。首先要梳理一下整个流程:
1)设置步长 l r lr lr,动量值 g a m m a gamma gamma,迭代次数 e p o c h s epochs epochs,batch_size等信息,(如果需要)设置初始权重 w 0 w_{0} w0,
2)导入数据,将数据切分成batches
3)定义神经网络架构
4)定义损失函数 L ( w ) L(w) L(w),如果需要的话,将损失函数调整成凸函数,以便求解最小值
5)定义所使用的优化算法
6)开始在epoches和batch上循环,执行优化算法:
6.1)调整数据结构,确定数据能够在神经网络、损失函数和优化算法中顺利运行
6.2)完成向前传播,计算初始损失
6.3)利用反向传播,在损失函数 L ( w ) L(w) L(w)上对每一个 w w w求偏导数
6.4)迭代当前权重
6.5)清空本轮梯度
6.6)完成模型进度与效果监控
7)输出结果
1 导库,设置各种初始值
import torch
from torch import nn
from torch import optim
from torch.nn import functional as F
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
#确定数据、确定优先需要设置的值
lr = 0.15
gamma = 0.8
epochs = 5
bs = 128
2 导入数据,分割小批量
以往我们的做法是:
#torch.manual_seed(420)
#X = torch.rand((50000,20),dtype=torch.float32) * 100 #要进行迭代了,增加样本数量
#y = torch.randint(low=0,high=3,size=(50000,1),dtype=torch.float32)
#data = TensorDataset(X,y)
#data_withbatch = DataLoader(data,batch_size=bs, shuffle = True)
这次我们要使用PyTorch中自带的数据,MINST-FATION。
import torchvision
import torchvision.transforms as transforms
#初次运行时会下载,需要等待较长时间
mnist = torchvision.datasets.FashionMNIST(
root='/Users/zhucan/Desktop/FashionMNIST'
, train=True
, download=True
, transform=transforms.ToTensor())
len(mnist) #查看特征张量
#60000
mnist.data
#tensor([[[0, 0, 0, ..., 0, 0, 0],
# [0, 0, 0, ..., 0, 0, 0],
# [0, 0, 0, ..., 0, 0, 0],
# ...,
# [0, 0, 0, ..., 0, 0, 0],
# [0, 0, 0, ..., 0, 0, 0],
# [0, 0, 0, ..., 0, 0, 0]],
#
# [[0, 0, 0, ..., 0, 0, 0],
# [0, 0, 0, ..., 0, 0, 0],
# [0, 0, 0, ..., 0, 0, 0],
# ...,
# [0, 0, 0, ..., 0, 0, 0],
# [0, 0, 0, ..., 0, 0, 0],
# [0, 0, 0, ..., 0, 0, 0]]], dtype=torch.uint8)
#这个张量结构看起来非常常规,可惜的是它与我们要输入到模型的数据结构有差异
mnist.data.shape
#torch.Size([60000, 28, 28])
#查看标签
mnist.targets
#tensor([9, 0, 0, ..., 3, 0, 5])
#查看标签的类别
mnist.classes
#['T-shirt/top',
# 'Trouser',
# 'Pullover',
# 'Dress',
# 'Coat',
# 'Sandal',
# 'Shirt',
# 'Sneaker',
# 'Bag',
# 'Ankle boot']
#查看图像的模样
mnist[0]
#(tensor([[[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0039, 0.0000, 0.0000, 0.0510,
# 0.2863, 0.0000, 0.0000, 0.0039, 0.0157, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0039, 0.0039, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0118, 0.0000, 0.1412, 0.5333,
# 0.4980, 0.2431, 0.2118, 0.0000, 0.0000, 0.0000, 0.0039, 0.0118,
# 0.0157, 0.0000, 0.0000, 0.0118],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0235, 0.0000, 0.4000, 0.8000,
# 0.6902, 0.5255, 0.5647, 0.4824, 0.0902, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0471, 0.0392, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.6078, 0.9255,
# 0.8118, 0.6980, 0.4196, 0.6118, 0.6314, 0.4275, 0.2510, 0.0902,
# 0.3020, 0.5098, 0.2824, 0.0588],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0039, 0.0000, 0.2706, 0.8118, 0.8745,
# 0.8549, 0.8471, 0.8471, 0.6392, 0.4980, 0.4745, 0.4784, 0.5725,
# 0.5529, 0.3451, 0.6745, 0.2588],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0039, 0.0039, 0.0039, 0.0000, 0.7843, 0.9098, 0.9098,
# 0.9137, 0.8980, 0.8745, 0.8745, 0.8431, 0.8353, 0.6431, 0.4980,
# 0.4824, 0.7686, 0.8980, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.7176, 0.8824, 0.8471,
# 0.8745, 0.8941, 0.9216, 0.8902, 0.8784, 0.8706, 0.8784, 0.8667,
# 0.8745, 0.9608, 0.6784, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.7569, 0.8941, 0.8549,
# 0.8353, 0.7765, 0.7059, 0.8314, 0.8235, 0.8275, 0.8353, 0.8745,
# 0.8627, 0.9529, 0.7922, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0039, 0.0118, 0.0000, 0.0471, 0.8588, 0.8627, 0.8314,
# 0.8549, 0.7529, 0.6627, 0.8902, 0.8157, 0.8549, 0.8784, 0.8314,
# 0.8863, 0.7725, 0.8196, 0.2039],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0235, 0.0000, 0.3882, 0.9569, 0.8706, 0.8627,
# 0.8549, 0.7961, 0.7765, 0.8667, 0.8431, 0.8353, 0.8706, 0.8627,
# 0.9608, 0.4667, 0.6549, 0.2196],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0157, 0.0000, 0.0000, 0.2157, 0.9255, 0.8941, 0.9020,
# 0.8941, 0.9412, 0.9098, 0.8353, 0.8549, 0.8745, 0.9176, 0.8510,
# 0.8510, 0.8196, 0.3608, 0.0000],
# [0.0000, 0.0000, 0.0039, 0.0157, 0.0235, 0.0275, 0.0078, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.9294, 0.8863, 0.8510, 0.8745,
# 0.8706, 0.8588, 0.8706, 0.8667, 0.8471, 0.8745, 0.8980, 0.8431,
# 0.8549, 1.0000, 0.3020, 0.0000],
# [0.0000, 0.0118, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.2431, 0.5686, 0.8000, 0.8941, 0.8118, 0.8353, 0.8667,
# 0.8549, 0.8157, 0.8275, 0.8549, 0.8784, 0.8745, 0.8588, 0.8431,
# 0.8784, 0.9569, 0.6235, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0706, 0.1725, 0.3216, 0.4196,
# 0.7412, 0.8941, 0.8627, 0.8706, 0.8510, 0.8863, 0.7843, 0.8039,
# 0.8275, 0.9020, 0.8784, 0.9176, 0.6902, 0.7373, 0.9804, 0.9725,
# 0.9137, 0.9333, 0.8431, 0.0000],
# [0.0000, 0.2235, 0.7333, 0.8157, 0.8784, 0.8667, 0.8784, 0.8157,
# 0.8000, 0.8392, 0.8157, 0.8196, 0.7843, 0.6235, 0.9608, 0.7569,
# 0.8078, 0.8745, 1.0000, 1.0000, 0.8667, 0.9176, 0.8667, 0.8275,
# 0.8627, 0.9098, 0.9647, 0.0000],
# [0.0118, 0.7922, 0.8941, 0.8784, 0.8667, 0.8275, 0.8275, 0.8392,
# 0.8039, 0.8039, 0.8039, 0.8627, 0.9412, 0.3137, 0.5882, 1.0000,
# 0.8980, 0.8667, 0.7373, 0.6039, 0.7490, 0.8235, 0.8000, 0.8196,
# 0.8706, 0.8941, 0.8824, 0.0000],
# [0.3843, 0.9137, 0.7765, 0.8235, 0.8706, 0.8980, 0.8980, 0.9176,
# 0.9765, 0.8627, 0.7608, 0.8431, 0.8510, 0.9451, 0.2549, 0.2863,
# 0.4157, 0.4588, 0.6588, 0.8588, 0.8667, 0.8431, 0.8510, 0.8745,
# 0.8745, 0.8784, 0.8980, 0.1137],
# [0.2941, 0.8000, 0.8314, 0.8000, 0.7569, 0.8039, 0.8275, 0.8824,
# 0.8471, 0.7255, 0.7725, 0.8078, 0.7765, 0.8353, 0.9412, 0.7647,
# 0.8902, 0.9608, 0.9373, 0.8745, 0.8549, 0.8314, 0.8196, 0.8706,
# 0.8627, 0.8667, 0.9020, 0.2627],
# [0.1882, 0.7961, 0.7176, 0.7608, 0.8353, 0.7725, 0.7255, 0.7451,
# 0.7608, 0.7529, 0.7922, 0.8392, 0.8588, 0.8667, 0.8627, 0.9255,
# 0.8824, 0.8471, 0.7804, 0.8078, 0.7294, 0.7098, 0.6941, 0.6745,
# 0.7098, 0.8039, 0.8078, 0.4510],
# [0.0000, 0.4784, 0.8588, 0.7569, 0.7020, 0.6706, 0.7176, 0.7686,
# 0.8000, 0.8235, 0.8353, 0.8118, 0.8275, 0.8235, 0.7843, 0.7686,
# 0.7608, 0.7490, 0.7647, 0.7490, 0.7765, 0.7529, 0.6902, 0.6118,
# 0.6549, 0.6941, 0.8235, 0.3608],
# [0.0000, 0.0000, 0.2902, 0.7412, 0.8314, 0.7490, 0.6863, 0.6745,
# 0.6863, 0.7098, 0.7255, 0.7373, 0.7412, 0.7373, 0.7569, 0.7765,
# 0.8000, 0.8196, 0.8235, 0.8235, 0.8275, 0.7373, 0.7373, 0.7608,
# 0.7529, 0.8471, 0.6667, 0.0000],
# [0.0078, 0.0000, 0.0000, 0.0000, 0.2588, 0.7843, 0.8706, 0.9294,
# 0.9373, 0.9490, 0.9647, 0.9529, 0.9569, 0.8667, 0.8627, 0.7569,
# 0.7490, 0.7020, 0.7137, 0.7137, 0.7098, 0.6902, 0.6510, 0.6588,
# 0.3882, 0.2275, 0.0000, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1569,
# 0.2392, 0.1725, 0.2824, 0.1608, 0.1373, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
# 0.0000, 0.0000, 0.0000, 0.0000]]]),
# 9)
import matplotlib.pyplot as plt
plt.imshow(mnist[0][0].view((28, 28)).numpy()); #imageshow
plt.imshow(mnist[1][0].view((28, 28)).numpy());
#分割batch
batchdata = DataLoader(mnist,batch_size=bs, shuffle = True) #总共多少个batch?
len(batchdata) #查看会放入进行迭代的数据结构
#15
for x,y in batchdata:
print(x.shape)
print(y.shape)
break
#torch.Size([4000, 1, 28, 28])
#torch.Size([4000])
input_ = mnist.data[0].numel() #特征的数目,一般是第一维之外的所有维度相乘的数
output_ = len(mnist.targets.unique()) #分类的数目
#最好确认一下没有错误
input_
#784
output_
#10
#==================简洁代码====================
import torchvision
import torchvision.transforms as transforms
mnist = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST'
, train=True
, download=False
, transform=transforms.ToTensor())
batchdata = DataLoader(mnist,batch_size=bs, shuffle = True)
input_ = mnist.data[0].numel()
output_ = len(mnist.targets.unique())
3 定义神经网络的架构
#定义神经网路的架构
class Model(nn.Module):
def __init__(self,in_features=10,out_features=2):
super().__init__()
#self.normalize = nn.BatchNorm2d(num_features=1)
self.linear1 = nn.Linear(in_features,128,bias=False)
self.output = nn.Linear(128,out_features,bias=False)
def forward(self, x):
#x = self.normalize(x)
x = x.view(-1, 28*28)
#需要对数据的结构进行一个改变,这里的“-1”代表,我不想算,请pytorch帮我计算
sigma1 = torch.relu(self.linear1(x))
z2 = self.output(sigma1)
sigma2 = F.log_softmax(z2,dim=1)
return sigma2
4 定义训练函数
def fit(net,batchdata,lr=0.01,epochs=5,gamma=0):
criterion = nn.NLLLoss() #定义损失函数
opt = optim.SGD(net.parameters(), lr=lr,momentum=gamma) #定义优化算法
correct = 0
samples = 0
for epoch in range(epochs):
for batch_idx, (x,y) in enumerate(batchdata):
y = y.view(x.shape[0])
sigma = net.forward(x)
loss = criterion(sigma,y)
loss.backward()
opt.step()
opt.zero_grad()
#求解准确率
yhat = torch.max(sigma,1)[1]
correct += torch.sum(yhat == y)
samples += x.shape[0]
if (batch_idx+1) % 125 == 0 or batch_idx == len(batchdata)-1:
print('Epoch{}:[{}/{}({:.0f}%)]\tLoss:{:.6f}\t Accuracy:{:.3f}'.format(
epoch+1
,samples
,len(batchdata.dataset)*epochs
,100*samples/(len(batchdata.dataset)*epochs)
,loss.data.item()
,float(correct*100)/samples))
5 进行训练与评估
#实例化神经网络,调用优化算法需要的参数
torch.manual_seed(420)
net = Model(in_features=input_, out_features=output_)
fit(net,batchdata,lr=lr,epochs=epochs,gamma=gamma)
#Epoch1:[16000/300000(5%)] Loss:0.314621 Accuracy:88.287
#Epoch1:[32000/300000(11%)] Loss:0.377433 Accuracy:88.159
#Epoch1:[48000/300000(16%)] Loss:0.380144 Accuracy:88.148
#Epoch1:[60000/300000(20%)] Loss:0.310791 Accuracy:88.140
#Epoch2:[76000/300000(25%)] Loss:0.273138 Accuracy:88.292
#Epoch2:[92000/300000(31%)] Loss:0.311703 Accuracy:88.390
#Epoch2:[108000/300000(36%)] Loss:0.256979 Accuracy:88.397
#Epoch2:[120000/300000(40%)] Loss:0.302862 Accuracy:88.426
#Epoch3:[136000/300000(45%)] Loss:0.215847 Accuracy:88.585
#Epoch3:[152000/300000(51%)] Loss:0.330663 Accuracy:88.638
#Epoch3:[168000/300000(56%)] Loss:0.219652 Accuracy:88.644
#Epoch3:[180000/300000(60%)] Loss:0.352059 Accuracy:88.672
#Epoch4:[196000/300000(65%)] Loss:0.294500 Accuracy:88.699
#Epoch4:[212000/300000(71%)] Loss:0.370549 Accuracy:88.747
#Epoch4:[228000/300000(76%)] Loss:0.331915 Accuracy:88.813
#Epoch4:[240000/300000(80%)] Loss:0.371244 Accuracy:88.828
#Epoch5:[256000/300000(85%)] Loss:0.303841 Accuracy:88.883
#Epoch5:[272000/300000(91%)] Loss:0.293404 Accuracy:88.950
#Epoch5:[288000/300000(96%)] Loss:0.193660 Accuracy:88.986
#Epoch5:[300000/300000(100%)] Loss:0.289494 Accuracy:88.994
我们现在已经完成了一个最基本的、神经网络训练并查看训练结果的代码,是不是感觉已经获得了很多支持呢?我们的模型最后得到的结果属于中规中矩,毕竟我们设置的网格结构只是最普通的全连接层,并且我们并没有对数据进行任何的处理或增强(在神经网络架构中,有被注释掉的两行关于batch normalization的代码,取消注释,你会看到神经网络的准确率瞬间增加了5%,这是常用的处理之一)。已经成熟的、更加稳定的神经网络架构可以很轻易在MINST-FASHION数据集上获得99%的准确率,因此我们还有很长的路要走。从下节课开始,我们将学习更完整的训练流程,并学习神经网络性能与效果优化相关的更多内容。
