nn.Conv1d\nn.Conv2d以及groups\dilation参数的理解

nn.Conv1d

代码:

nn.Conv1d(in_channels = 16, out_channels = 16, kernel_size = (3,2,2), stride = (2,2,1), padding = [2,2,2])

如果输入为:

x = torch.randn(10,16,30,32,34)

则:

• 10代表:batch_size
• 16代表:输入的通道数
• 30，32，34代表图片(或其他)的大小

那么经过这个nn，输出的规格为[10,16,16,18,37]
公式如下:
$$d_{out}=(d_{in}-kerne{l}_{s}ize+2\ast padding)/stride+1)$$

• (30- 3 + 2*2) / 2 + 1 = 16
• (32 - 2 + 2*2) / 2 + 1 = 18
• (34 - 2 + 2*2) / 1 + 1 = 37

可以理解为: 大小为3/3/2的三个卷积核，分别在输入图片的三个维度上，进行滑动

nn.Conv2d

代码:

nn.Conv2d(16, 32 , kernel_size(3,2), stride = (2,1))

如果输入为:

x = torch.rand(10,16,30,32)

则输出规格为[10,32,14,31]:

• 10 : batch_size
• 32 : 输出通道数
• (30 - 3 + 2 * 0)/ 2 + 1 = 14
• (32 - 2 + 2*0)/1 + 1 = 31

nn.Conv2d中groups参数和dilation参数的理解

groups

当groups=1的时候，假设此时 输入的通道数为n，输出的通道数为m，那么理解为把输入的通道分成1组(不分组)，每一个输出通道需要在所有的输入通道上做卷积，也就是一种参数共享的局部全连接。
如果把groups改成2，可以理解为把 输入的通道分成两组，此时每一个输出通道只需要在其中一组上做卷积。
如果groups=in_channels，也就是把 输入的通道分成in_channels组(每一组也就一个通道)，此时每一个输出通道只需要在其中一个输入通道上做卷积。

dilation

conv_arithmetic
dilation体现了一种叫做à trous的思想，引入dilation后的输出计算公式为 ：

$$d_{out}=(d_{in}-dilation\ast (kernelsize-1)-1+2\ast padding)/stride+1)$$
更新(2021/1/6-23:45):这个公式可以这样理解:
引入了dilation之后，整个的new_kernelsize就变成了
$$new\_kernelsize=dilation\ast (kernelsize-1)+1$$
所以
$$d_{out}=(d_{in}-new\_kernelsize+2\ast padding)/stride+1)$$
我们定义一个3 * 3的卷积核，如果dilation参数为默认(1),那就是按照常规理解来做卷积，如下图所示:

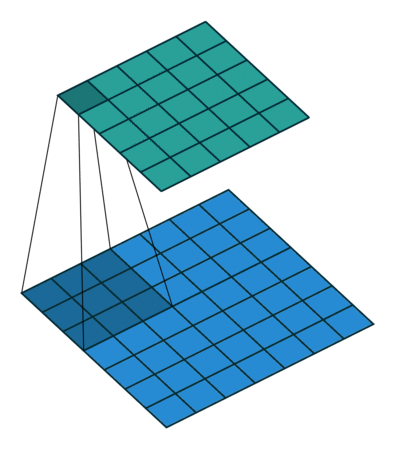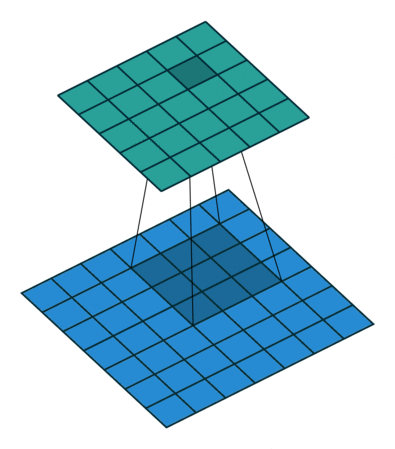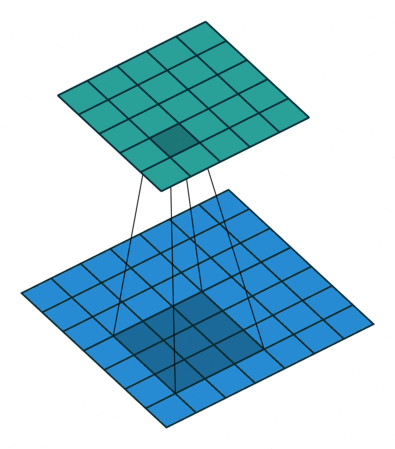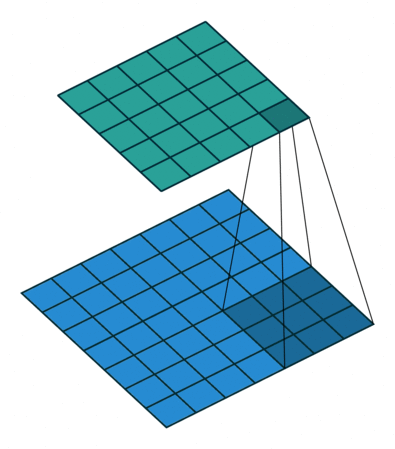
如果我们把dilation设置成2，其实也就是在两两卷积点中插入一个空白，使得3*3的卷积核，变为了5 * 5:

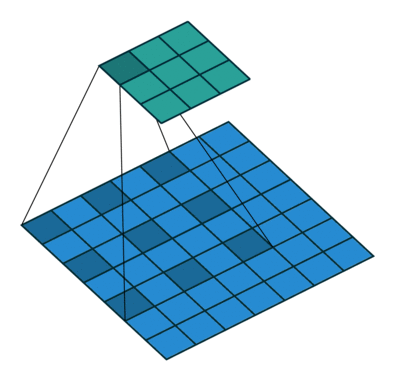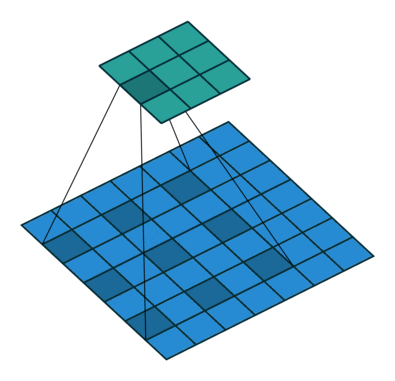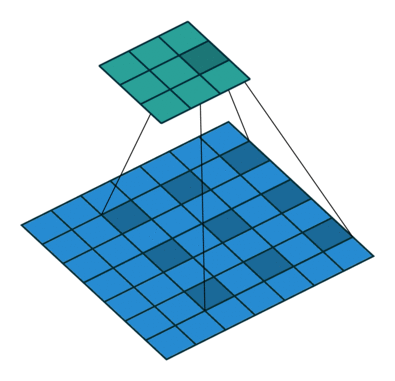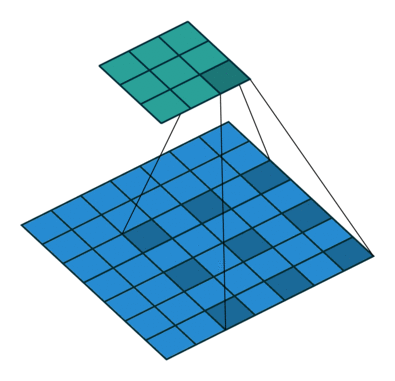
dilation = 1:

import torch.nn as nn
m = nn.Conv2d(1, 1, (3, 3), dilation=(1, 1))  # `dilation=(1,1)` = `dilation=1`
input = torch.randn(1, 1, 7, 7)
output = m(input)
print(output.shape)
>>>输出:[1,1,5,5]

dilation = 2:

import torch.nn as nn
m = nn.Conv2d(1, 1, (3, 3), dilation=(2, 2))  # `dilation=(2,2)` = `dilation=2`
input = torch.randn(1, 1, 7, 7)
output = m(input)
print(output.shape)
>>>输出:[1,1,3,3]

参考

conv_arithmetic
pytorch官网