python面积图之曲线图的填充

目录

• 基础用法
• 案例
• 复杂的fille_between(案例来源官网)
• where和interpolate
• where
• interpolate
• step

用法：

Axes.fill_between(x, y1, y2=0, where=None, interpolate=False, step=None, *, data=None, **kwargs)

参数说明：

基础用法

import matplotlib.pyplot as plt
import numpy as np
x = [1, 2, 3, 4, 5]
y1 = [1, 4, 9, 16, 25]
y2 = [9, 9, 9, 9, 9]
fig, (ax1, ax2) = plt.subplots(1,2)
ax1.fill_between(x, y1, alpha=.5, linewidth=0)
ax1.set_title('填充x,y1之间')
ax2.fill_between(x, y2, alpha=.5, linewidth=1)
ax2.set_title('填充x,y2之间')
plt.show()

当然这样时没有多大意义的,只是想展示出一个比较明确的填充,类似于区域全部填充颜色

案例

import matplotlib.pyplot as plt
import numpy as np

np.random.seed(1)
x = np.linspace(0, 8, 16)
y1 = 3 + 4*x/8 + np.random.uniform(0.0, 0.5, len(x))
y2 = 1 + 2*x/8 + np.random.uniform(0.0, 0.5, len(x))
fig, ax = plt.subplots()
ax.fill_between(x, y1, y2, alpha=.5, linewidth=0)
ax.plot(x, (y1 + y2)/2, linewidth=2)

ax.set(xlim=(0, 8), xticks=np.arange(1, 8),
       ylim=(0, 8), yticks=np.arange(1, 8))
plt.show()

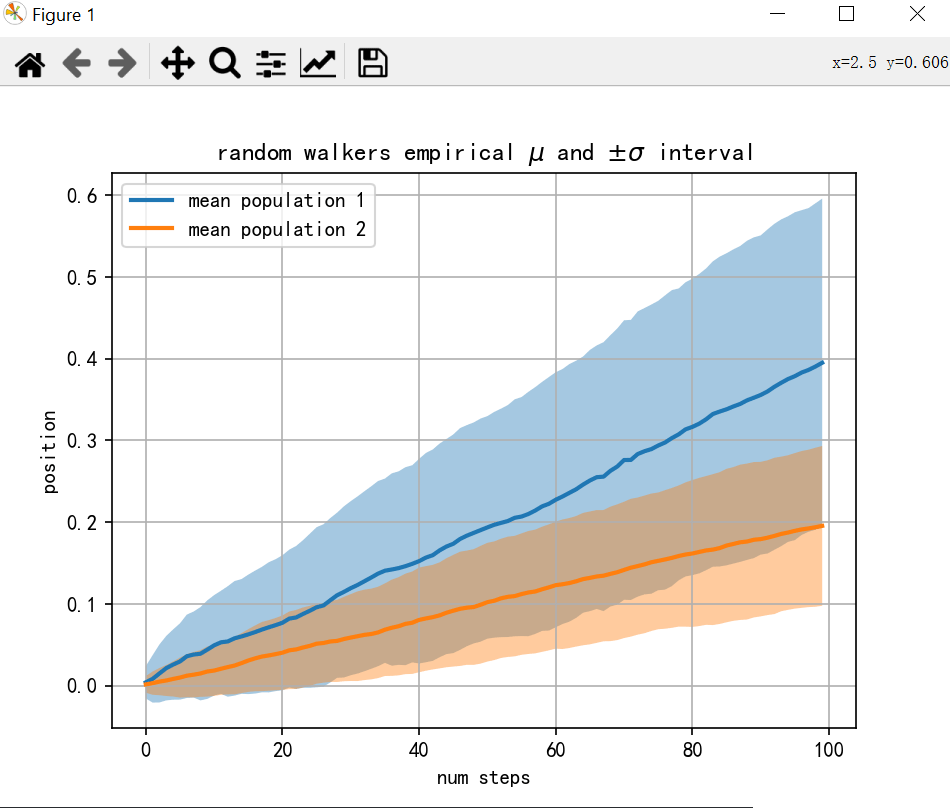
复杂的fille_between(案例来源官网)

import numpy as np
import matplotlib.pyplot as plt

Nsteps, Nwalkers = 100, 250
t = np.arange(Nsteps)
# an (Nsteps x Nwalkers) array of random walk steps
S1 = 0.004 + 0.02*np.random.randn(Nsteps, Nwalkers)
S2 = 0.002 + 0.01*np.random.randn(Nsteps, Nwalkers)
# an (Nsteps x Nwalkers) array of random walker positions
X1 = S1.cumsum(axis=0)
X2 = S2.cumsum(axis=0)
# Nsteps length arrays empirical means and standard deviations of both
# populations over time
mu1 = X1.mean(axis=1)
sigma1 = X1.std(axis=1)
mu2 = X2.mean(axis=1)
sigma2 = X2.std(axis=1)
# plot it!
fig, ax = plt.subplots(1)
ax.plot(t, mu1, lw=2, label='mean population 1')
ax.plot(t, mu2, lw=2, label='mean population 2')
ax.fill_between(t, mu1+sigma1, mu1-sigma1, facecolor='C0', alpha=0.4)
ax.fill_between(t, mu2+sigma2, mu2-sigma2, facecolor='C1', alpha=0.4)
ax.set_title(r'random walkers empirical $\mu$ and $\pm \sigma$ interval')
ax.legend(loc='upper left')
ax.set_xlabel('num steps')
ax.set_ylabel('position')
ax.grid()

where和interpolate

where

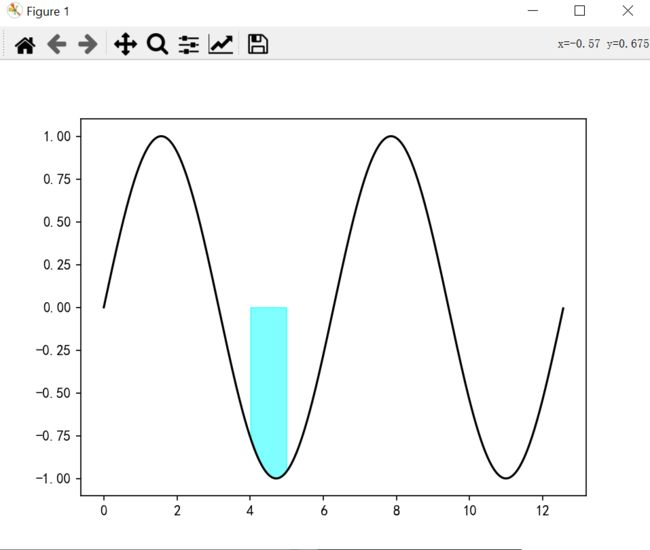
定义从何处排除要填充的某些水平区域。填充区域由坐标x[其中]定义。更准确地说，如果其中[i]和其中[i+1]，则在x[i]和x[i+1]之间填充。请注意，此定义意味着where中两个假值之间的孤立真值不会导致填充。由于相邻的假值，真实位置的两侧仍保持未填充状态。

import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots()
x = np.arange(0, 4 * np.pi, 0.01)
y = np.sin(x)
ax.plot(x, y, color='black')
ax.fill_between(x, y, 0, where=(x>4)&(x<5),color='cyan', alpha=0.5)
plt.show()

interpolate

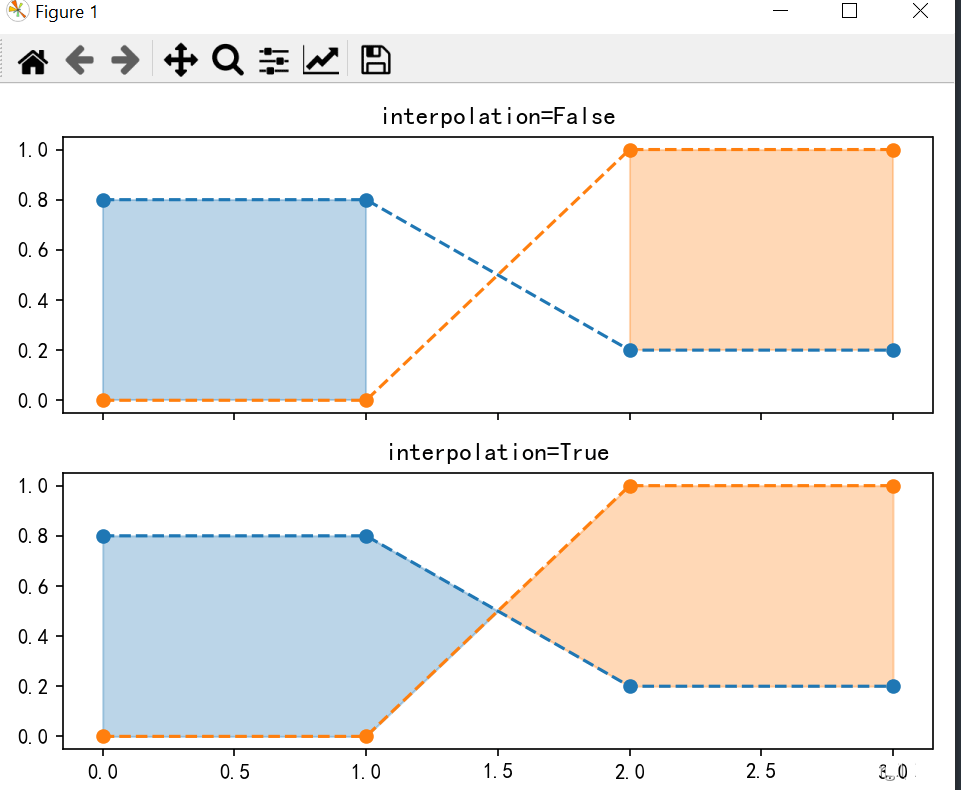
在语义上，where通常用于y1>y2或类似的词。默认情况下，定义填充区域的多边形节点将仅放置在x阵列中的位置。这样的多边形无法描述上述靠近交点的语义。包含交叉点的x截面仅被剪裁。
将“插值”设置为True将计算实际交点，并将填充区域延伸到此点。

import numpy as np
import matplotlib.pyplot as plt

x = np.array([0, 1, 2, 3])
y1 = np.array([0.8, 0.8, 0.2, 0.2])
y2 = np.array([0, 0, 1, 1])

fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
ax1.set_title('interpolation=False')
ax1.plot(x, y1, 'o--')
ax1.plot(x, y2, 'o--')
ax1.fill_between(x, y1, y2, where=(y1 > y2), color='C0', alpha=0.3)
ax1.fill_between(x, y1, y2, where=(y1 < y2), color='C1', alpha=0.3)
ax2.set_title('interpolation=True')
ax2.plot(x, y1, 'o--')
ax2.plot(x, y2, 'o--')
ax2.fill_between(x, y1, y2, where=(y1 > y2), color='C0', alpha=0.3,
                 interpolate=True)
ax2.fill_between(x, y1, y2, where=(y1 <= y2), color='C1', alpha=0.3,                interpolate=True)
fig.tight_layout()

step

包含参数为三个{‘pre’,‘post’,‘mid’}
如果填充应为阶跃函数，即x之间的常数，则定义阶跃。该值确定阶跃发生的位置：

• “pre”：y值从每个x位置持续向左，即间隔（x[i-1]，x[i]]的值为y[i]。
• “post”：y值从每个x位置持续向右，即区间[x[i]，x[i+1]）的值为y[i]。
• “mid”：步数出现在x位置的中间。

import numpy as np
import matplotlib.pyplot as plt

a = np.linspace(0,2*3.14,50) 
b = np.sin(a) 
plt.figsize=((12,6))
plt.subplot(131)
plt.fill_between(a, b, 0, where = (a > 2) & (a < 5), color = 'green', step='pre') 
plt.plot(a,b)
plt.title('step=pre')

plt.subplot(132)
plt.fill_between(a, b, 0, where = (a > 2) & (a < 5), color = 'cyan', step='post') 
plt.plot(a,b)
plt.title('step=post')

plt.subplot(133)
plt.fill_between(a, b, 0, where = (a > 2) & (a < 5), color = 'red', step='mid') 
plt.plot(a,b)
plt.title('step=mid')
plt.show()

偏移会有点不一样,因为函数的缘故,偏移不太明显

到此这篇关于python面积图之曲线图的填充的文章就介绍到这了,更多相关python曲线填充内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！