线性回归算法之鸢尾花特征分类【机器学习】

一.前言

1.1 本文原理

线性回归就是用一条直线来准确描述数据之间的关系，这样当新数据出现时，就可以预测一个简单的值。一般来说，就是将真实数据映射到坐标轴上，坐标轴上的数据呈线性形状，然后构建一个函数，使函数对应的数据尽可能接近真实数据，使函数在坐标轴上绘制的图像尽可能通过真实数据中的所有点，并尝试最小化我们构建的函数所表示的坐标轴上所有点和线之间的距离。

1.1 本文目的

• 使用scikit-learn机器学习包的线性回归算法，对鸢尾花进行分类；
• 使用scikit-learn机器学习包的线性回归算法，选择一个特征对鸢尾花进行分类；
• 使用scikit-learn机器学习包的线性回归算法，选择两个特征对鸢尾花进行分类；
• 使用scikit-learn机器学习包的线性回归算法，选择三个特征对鸢尾花进行分类；
  结合上一个数据分析和可视化实验，根据对鸢尾花数据的特征两两对比可视化图，分析特征可视化对特征选择及相关分类计算结果的影响；
• 熟悉机器学习线性回归算法
• 使用线性回归算法解决问题
  

二.实验过程

2.1使用scikit-learn机器学习包的算法，对鸢尾花进行分类

相信各位，经过上文的学习，我们已经安装了scikit-learn机器学习包。

我们先导入鸢尾花特征数据包如下：
load_iris模块里有150组鸢尾花特征数据供我们学习使用。

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
print(X.shape, X)
y = iris.target
print(y.shape, y)

下面我们对对鸢尾花进行分类。
使用plt.scatter绘制散点图，我们看一下里面的参数。
看一下他的文档：

matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None,
vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, hold=None, data=None, **kwargs)

feature = 1
feature_other = 2
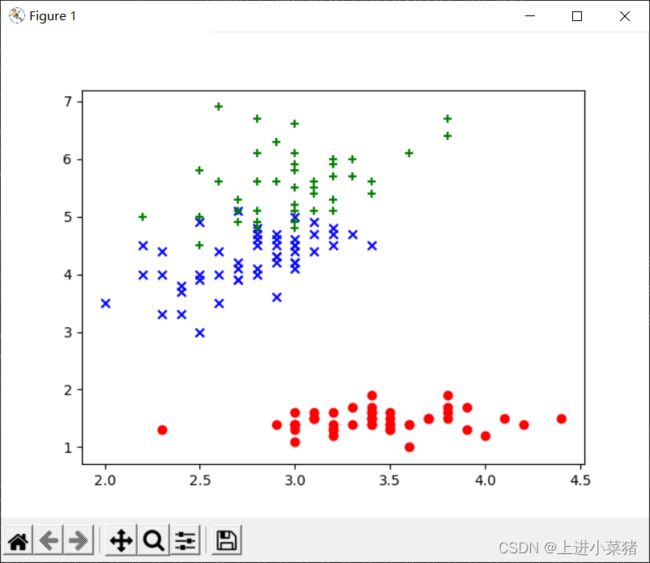
plt.scatter(X[0:50,feature], X[0:50,feature_other], color='red', marker='o', label='setosa') #前50个样本
plt.scatter(X[50:100,feature], X[50:100,feature_other], color='blue', marker='x', label='versicolor') #中间50个
plt.scatter(X[100:,feature], X[100:,feature_other],color='green', marker='+', label='Virginica') #后50个样本
plt.show()

上述代码解释：
feature为1，feature_other为2，使用scatter绘制散点图，我们分别使用它的前50个样本，中间50个，后50个样本，采用第二个特征和第三个特征。

plt.show()显示散点图：

2.2 使用scikit-learn机器学习包的线性回归算法，选择一个特征对鸢尾花进行分类

导入numpy模块，拟合运算需要;

import numpy as np

我们需要先导入linear_model模块，之后再创建一个线性模型。

from sklearn import linear_model

最小二乘法线性回归

linear_model.LinearRegression(fit_intercept=True, normalize=False,copy_X=True, n_jobs=1)

根据第一个特征进行拟合：

linear.fit(X[:,:1],y)

输出线性回归一个特征拟合得分：

print("线性回归 training score: ",linear.score(X[:,:1],y))

可视化看一下;

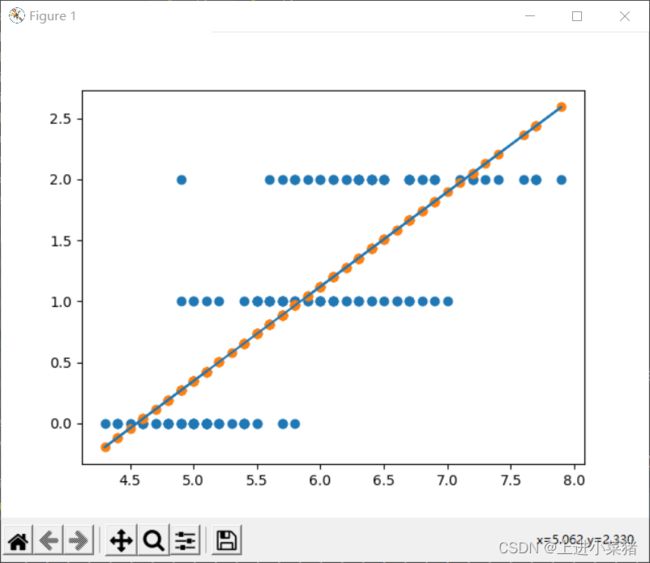
plt.scatter(X[:,:1],y)
plt.scatter(X[:,:1],np.dot(X[:,:1],linear.coef_)+linear.intercept_)
plt.plot(X[:,:1],np.dot(X[:,:1],linear.coef_)+linear.intercept_)
plt.show()

可视化结果为：

2.3 使用scikit-learn机器学习包的线性回归算法，选择两个特征对鸢尾花进行分类

使用循环取出两个不同特征进行训练。
循环训练得分如下：

for j in range(4):
    if i

2.4 使用scikit-learn机器学习包的线性回归算法，选择三个特征对鸢尾花进行分类；

写第4项代码，循环取出三个不同特征进行训练。
循环训练得分如下：

for j in range(4):
if i

2.5 结合上一个数据分析和可视化实验，根据对鸢尾花数据的特征两两对比可视化图，分析特征可视化对特征选择及相关分类计算结果的影响

在俩个特征分析是最高为0.925，说明花瓣长度，花瓣宽度属性特征选择比重较大。
在三个特征分析是最高为0.93说明花萼长度，花瓣长度，花瓣宽度属性特征选择比重较大。
，其次为0.928，说明花萼宽度，花瓣长度，花瓣宽度这三个属性特征对计算结果的影响较大。