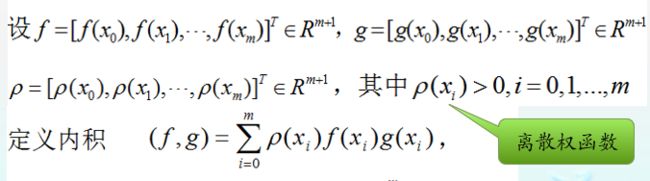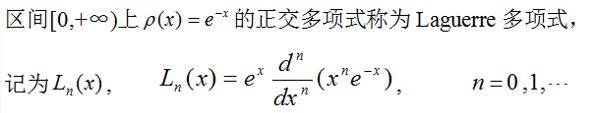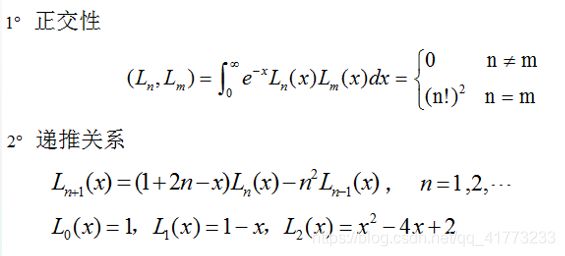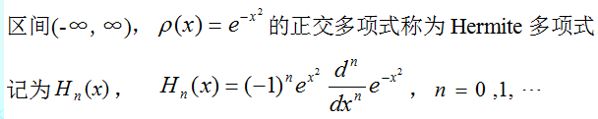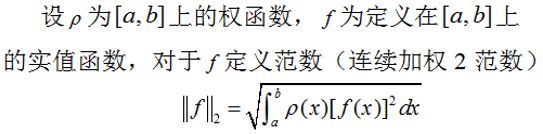数值分析(7)：函数逼近
函数逼近
- 1. 引言
- 2. 预备知识
- 3. 正交多项式
-
- 3.1 正交多项式的定义和性质
- 3.2 几个常用的正交多项式
- 4. 最佳平方逼近
- 5. 曲线拟合的最小二乘法
1. 引言
在前面章节《数值分析(6)：分段低次插值和三次样条插值》和《数值分析(5)：插值法》中已经介绍了如何用给定的插值点进行插值，得到的插值函数能够精确地经过这些给定的插值点。但是如果这些点本身就不精确，那么我们就没必要精确地经过这些点，只要保证在插值函数多项式的次数较低的情况下，和这些点保持一个较小的误差即可，即函数逼近。
首先来看代数多项式空间的概念：
再来看函数空间的概念：
显然函数空间是由函数组成的，满足加法和数乘运算的线性空间。
对于函数逼近，有以下的魏尔斯特拉斯定理
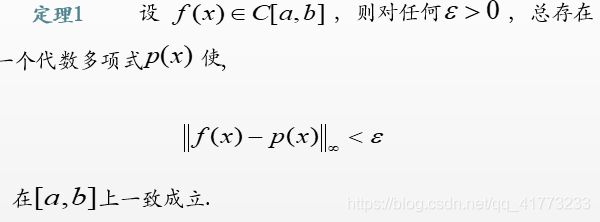伯恩斯坦1912年给出的证明是一种构造性证明.他根据函数整体逼近的特性构造出伯恩斯坦多项式，即：
其中：
这个结果不但证明了定理1，而且由(*)给出了
的一个逼近多项式，但它收敛太慢，实际中很少使用。
更一般的情况是，用函数空间的子空间 Φ \Phi Φ来求解一个函数 φ ∗ ( x ) \varphi^*(x) φ∗(x)来逼近原函数 f ( x ) f(x) f(x)，即：
本章的逼近问题即为：在某个函数空间 Φ \Phi Φ中求出 φ ( x ) \varphi(x) φ(x),使得：
最小，即曲线拟合的最小二乘法。
2. 预备知识
1.多元函数极值的必要条件：
偏导数等于0.(非充分条件)
2.向量内积的定义与其四条性质：
关于内积空间中的是否向量线性无关 （注意线性无关并不一定正交） ，可以用以下的gram矩阵判断，即：
3.权函数的定义与带权内积的定义
权函数的定义如下：
带权内积的定义如下：
可以证明，带权内积也满足内积的四条性质，那么根据带权内积可以定义连续加权⒉范数，即：
4.向量的加权内积
向量的加权内积定义如下
5.离散权函数的带权内积
离散权函数的带权内积定义如下：
离散加权2范数:
6.函数组的线性相关，线性无关
对于 i i i次多项式，有以下命题：
3. 正交多项式
3.1 正交多项式的定义和性质
根据前述的带权内积的定义，可以定义带权的正交多项式，也就是带权内积为0的多项式序列中的多项式。
如果一个多项式满足以下定义：
那么称该多项式序列 { φ n ( x ) , n ≥ 0 } \{ \varphi_n(x),n \geq0 \} {φn(x),n≥0}是在 [ a , b ] [a, b] [a,b]上带权函数 ρ ( x ) \rho(x) ρ(x)正交，并称 φ n ( x ) \varphi_n(x) φn(x)为 [ a , b ] [a, b] [a,b]上带权函数 ρ ( x ) \rho(x) ρ(x)的 n n n次正交多项式。
如果给定了区间 [ a , b ] [a, b] [a,b]和权函数 ρ ( x ) \rho(x) ρ(x)，那么构造正交多项式可以用以下方法：
其中：
C j = ( x n , φ j ( x ) ) ( φ j ( x ) , φ j ( x ) ) C_j=\frac{(x^n,\varphi_j(x))}{(\varphi_j(x),\varphi_j(x))} Cj=(φj(x),φj(x))(xn,φj(x))
正交多项式的性质有以下六条：
注意第六个性质是非常强的，n次多项式必有n个根，但是未必是不同的，实的，并且都被限制在某个区间内的。
3.2 几个常用的正交多项式
1.Legendre多项式
定义：
性质：
2.Chebyshev多项式
定义：
性质：
3.Laguerre多项式
定义：
性质：
4.Hermite多项式
定义：
4. 最佳平方逼近
在介绍最佳平方逼近之前，首先来看函数二范数的定义：
如果函数二范数是有界的，那么有如下记号：
如果空间 Φ \Phi Φ是空间 L ρ 2 [ a , b ] L^2_{\rho}[a,b] Lρ2[a,b]的子空间，那么空间 Φ \Phi Φ中的函数 s ( x ) s(x) s(x)可以记为：
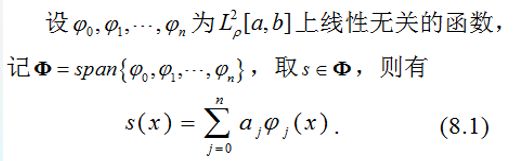
接下来开始正式地描述最佳平方逼近问题，最佳平方逼近函数的定义如下所示，如前所述，函数 f f f所处的空间 L ρ 2 [ a , b ] L^2_{\rho}[a,b] Lρ2[a,b]更大，而函数 s s s所处的空间 Φ \Phi Φ更小，最佳平方逼近所做的事情是用一个低维空间的函数去逼近 高维空间的函数，使得他们之间的平方误差最小。
最佳平方逼近问题的直观描述如下图所示：
接下来的问题是如何求解这个最佳平方逼近函数 s ∗ s^* s∗，因为 s ∗ ( x ) s^*(x) s∗(x)是 φ ( x ) \varphi(x) φ(x)的线性组合，而需要确定的只是 φ ( x ) \varphi(x) φ(x)前的系数，而需要去逼近的函数 f ( x ) f(x) f(x)是已知的，显然这就是一个求函数极值的问题，把待定系数当做自变量，而其他的部分当做已知量，求这个函数的极值，即：
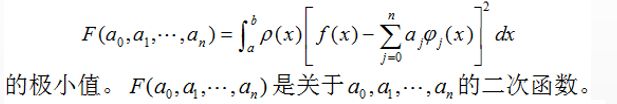
多元函数 F F F能取到极值的必要条件是对各个自变量的偏导数为0，即：
将函数 F F F的表达式代入后整理即得（其中用了一个小技巧就是求导和积分符号互换位置）：
由上图可知，法方程给定了待定系数 a j a_j aj的值，从而最佳平方逼近函数 s ∗ ( x ) s^*(x) s∗(x)就得到了求解。将上述法方程整理成矩阵的形式即为：
由于 φ j ( x ) \varphi_j(x) φj(x)是空间 L ρ 2 [ a , b ] L^2_{\rho}[a,b] Lρ2[a,b]的一组基，所以最佳平方逼近函数 s ∗ ( x ) s^*(x) s∗(x)的解唯一，即：
需要注意的是，虽然证明了 s ∗ ( x ) s^*(x) s∗(x)的存在性和唯一性，但 s ∗ ( x ) s^*(x) s∗(x)未必能使 F F F取得最小值，因为偏导数为0只是必要条件，并不是充分条件，下面还需要证明它能使 F F F取得最小值。
下面这张图给出了证明思路，只要证明 f − s ∗ f-s^* f−s∗与空间 Φ \Phi Φ中的任一函数 s s s正交，那么就可以证明 ∣ ∣ f − s ∗ ∣ ∣ ≤ ∣ ∣ f − s ∣ ∣ ||f-s^*|| \leq||f-s|| ∣∣f−s∗∣∣≤∣∣f−s∣∣
根据法方程可知：
上式也就说明了 f − s ∗ f-s^* f−s∗与空间 Φ \Phi Φ中的所有基函数正交，从而也就说明了与与空间 Φ \Phi Φ中的任意函数正交。从而证明就结束了， ∣ ∣ f − s ∗ ∣ ∣ ||f-s^*|| ∣∣f−s∗∣∣即为 ∣ ∣ f − s ∣ ∣ ||f-s|| ∣∣f−s∣∣的最小值。以上是从几何的角度给出的证明，用代数的角度给出证明如下：
逼近的误差称为最佳平方逼近误差，即：
对于最佳平方逼近函数，来考虑一种特殊的情况，即空间 Φ \Phi Φ是多项式函数组成的空间：
相应的待定系数可以通过法方程求解，即：
遗憾的是，虽然这个 Φ \Phi Φ空间的基足够简单，但是Hilbert矩阵是病态的，想要通过这个矩阵求解系数 a j ∗ a^*_j aj∗非常困难。因此为了简化法方程，通常采用Gram-Schemidt 方法将 Φ \Phi Φ空间的基转换为正交基，从而法方程的系数矩阵会变为一个对角矩阵，从而最佳平方逼近函数 s ∗ ( x ) s^*(x) s∗(x)可以写为：
上式中要求 φ j ( x ) \varphi_j(x) φj(x)是 Φ \Phi Φ空间的正交基。
5. 曲线拟合的最小二乘法
我们首先来看曲线拟合问题：
通过给定的离散数据，找一个函数（这个函数的次数由我们给定）能够使得其拟合的误差最小，显然，这就是最佳平方逼近的离散版本。
最小二乘法曲线拟合的数学定义如下：
解决最小二乘法曲线拟合问题，只需要定义一下离散版本的函数加权内积即可，即：
那么就有法方程来求解最小二乘解（即最佳平方逼近函数） s ∗ ( x ) s^*(x) s∗(x)
同理可以定义均方误差为：
如果给定的离散数据呈现出指数函数形态，那么最佳平方逼近函数 s ∗ ( x ) s^*(x) s∗(x)最好也具有指数函数形态，即：
其中 a , b a,b a,b为待定常数，直接求 a , b a,b a,b会出现非线性方程组，求解相当困难，因此先化成线性问题。通常办法是对(9.10）的两边取对数转换为线性问题，即：
当然，关于类似于指数函数的非多项式函数的拟合函数，有一些常见的做法如下：
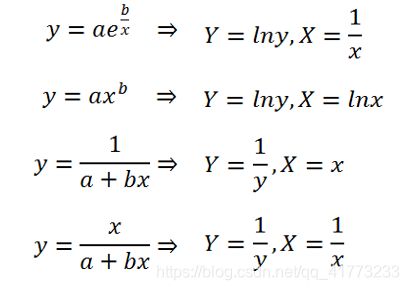
注:用多项式做最小二乘曲线拟合，法方程是病态方程组，此时可用正交多项式做最小二乘曲线拟合。
如果搞明白了最佳平方逼近问题，那么超定方程组的最小二乘解问题也就很自然地类比解决了，即：
参考文献：
关治，陆金甫《数值方法》