评价学习算法：欠拟合和过拟合，方差和偏差，学习曲线，不同神经网络架构优缺点

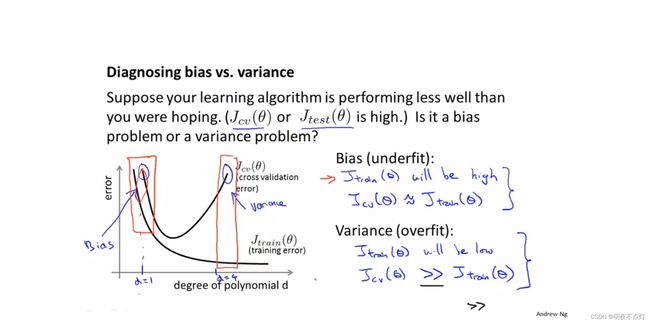
训练误差会随着多项式的次数增加而下降，交叉验证误差会随着多项式的次数的增加先下降后上升

过拟合和欠拟合的判断依据

1.如果训练误差很大，交叉验证误差也很大且约等于训练误差，则说明这是欠拟合的情况

2.如果训练误差较小，交叉验证误差很大且远远大于训练误差，则说明这是过度拟合的情况。

1.算法正则化可以有效防止过拟合的问题，正则化就是在代价方差函数之后添加一项，惩罚西塔参数，让西塔参数不至于过大

2.当正则化参数很大时，正则化项对参数西塔的惩罚很大，会导致欠拟合的情况发生。

3.当正则化参数较小时，正则化项对参数西塔几乎没有惩罚，会导致过度拟合的情况发生。 

模型选择在选取正则化参数兰达时的应用

选择参数的步骤如下：

1.列举出所有的正则化参数兰达

2.用训练集拟合参数分别最小化在每个兰达下的代价函数J，从而确定在每个兰达下的参数向量西塔

3.对于所求的参数用交叉验证集来评价它们得到模型，测出每一个参数向量西塔在交叉验证集上的平均方差

4.选取交叉验证集误差最小的参数模型

5.对所选择的参数模型观察其在测试集上的表现来检测其在新样本的泛化能力

 正则化参数兰达对训练误差和交叉验证误差的影响

1.训练误差不包括正则化项

2.训练误差在正则化参数兰达很小时较小因为对参数西塔的惩罚较小，在兰达很大时较大 因为对西塔的惩罚较大导致参数西塔较小。

3.交叉验证误差在兰达较小时较大，为高方差；在兰达较大时也较大，为高偏差。这两个模型的拟合效果不好。只有在中间合适位置最小，对新样本的拟合效果最好。

学习曲线

1.对于低阶拟合函数，当样本数量较少时，能够实现很好的拟合特性；当样本数量较多时，拟合程度下降；训练误差也会随着样本数量的增加而增大。

2. 当训练样本越多，函数拟合得就会越准确，就越具有规律性，越适合泛化样本，故交叉验证误差就会越小。

高偏差情况下

1.当学习算法处于高偏差 （参数较少但样本数量较多）时，随着训练样本的增加，交叉验证验差会由高慢慢下降直至稳定，训练误差会由低慢慢升高直至稳定，并且向交叉验证误差接近。

2.样本数量的增加对于高偏差的训练误差和交叉验证误差的变化不大。

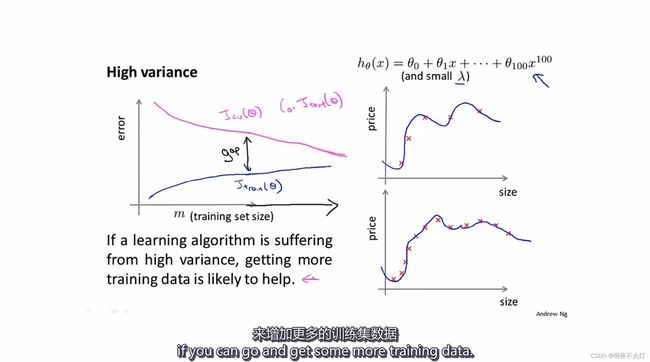
高方差情况

1.当参数较多处于高方次函数且正则化参数很小时，会出现过拟合，为高方差情况。

2.在样本数量较少时，过拟合情况会教严重；当样本数量较多时，由于曲线无法对每个样本数据都进行拟合，所以过拟合情况会减轻。

3.训练误差会随着训练样本数量的增加而逐渐增大，因为训练样本数量较多时无法对每一样本进行拟合。

4.交叉验证误差会随着训练样本数量的增加而较小，随着训练样本数量的增加，所拟合出来的曲线更具有代表性，因此泛化能力更强。

5.随着训练样本数量的增加，训练误差和交叉验证误差会逐渐接近。

 

对应的方法及解决的问题

方差：variane  偏差：bias 

 

 

不同神经网络架构的优劣

 

1.当神经网络架构较简单，参数和层数较少时，容易出现欠拟合情况，优点是计算量较小。

2.当神经网络架构较复杂，参数和层数较多时，容易出现过拟合和计算量过大的情况，但同时性能较好。当出现过拟合的情况时，可以调整正则化参数进行修正。