Java常见排序算法
Java常见排序算法
- 1. 排序算法概述
-
- 1.1 排序算法分类
- 1.2 排序算法总结
- 2. 排序算法
-
- 2.1 冒泡排序
- 2.2 快速排序
- 2.3 直接插入排序
- 2.4 希尔排序
- 2.5 简单选择排序
- 2.6 堆排序
- 2.7 归并排序
- 2.8 桶排序
- 2.9 计数排序
- 2.10 基数排序
1. 排序算法概述
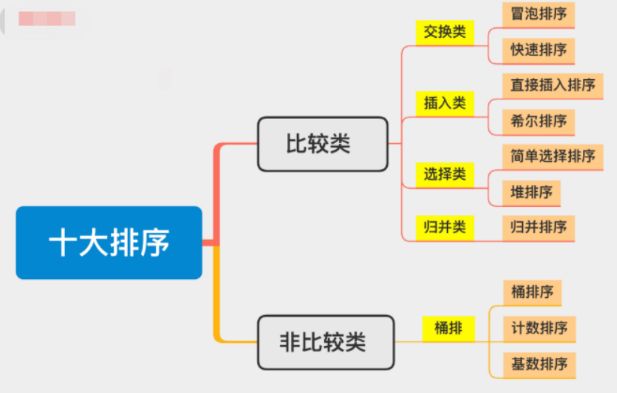
1.1 排序算法分类
数据结构与算法作为开发的基础是必不可少的技能,排序作为数据结构中比较重要且基础的能力。常见的排序算法按是否比较分为比较类与非比较类。
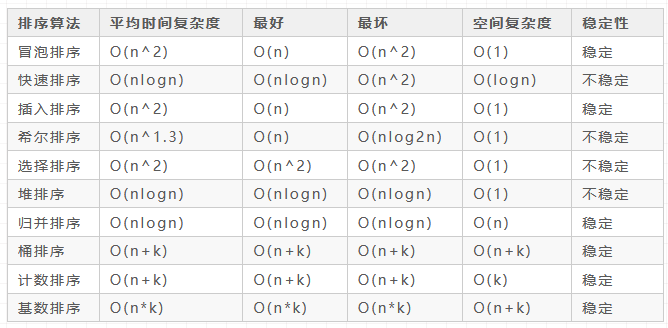
1.2 排序算法总结
2. 排序算法
2.1 冒泡排序
冒泡排序,又称起泡排序,它是一种基于交换的排序典型,也是快排思想的基础,冒泡排序是一种稳定排序算法,时间复杂度为O(n^2).基本思想是:「循环遍历多次每次从前往后把大元素往后调,每次确定一个最大(最小)元素,多次后达到排序序列。」(或者从后向前把小元素往前调)。
排序思想
从第一个元素开始往后遍历,每到一个位置判断是否比后面的元素大,如果比后面元素大,那么就交换两者大小,然后继续向后,这样的话进行一轮之后就可以保证「最大的那个数被交换交换到最末的位置可以确定」。
第二次同样从开始起向后判断着前进,如果当前位置比后面一个位置更大的那么就和他后面的那个数交换。但是有点注意的是,这次并不需要判断到最后,只需要判断到倒数第二个位置就行(因为第一次我们已经确定最大的在倒数第一,这次的目的是确定倒数第二)
同理,后面的遍历长度每次减一,直到第一个元素使得整个元素有序。
排序案例
例如2 5 3 1 4排序过程如下
第一趟排序:
第一次比较,因为2小于5所以不变:2 5 3 1 4
第二次比较,因为5大于3交换位置:2 3 5 1 4
第三次比较,因为5大于1交换位置:2 3 1 5 4
第四次比较,因为5大于4交换位置:2 3 1 4 5
至此完成第一趟排序:2 3 1 4 5
第二趟排序:21345
第三趟排序:12345
代码实现
/**
* 冒泡排序
*
* @param array 要排序的数组
*/
private static void bubbleSort(int[] array) {
for (int i = array.length - 1; i >= 0; i--) {
for (int j = 0; j < i; j++) {
// 如果array[j]>array[j+1],交换位置
if (array[j] > array[j + 1]) {
int variable = array[j];
array[j] = array[j + 1];
array[j + 1] = variable;
}
}
}
System.out.println("冒泡排序:" + JSON.toJSONString(array));
}
2.2 快速排序
快速排序是对冒泡排序的一种改进,采用递归分治的方法进行求解。而快排相比冒泡是一种不稳定排序,时间复杂度最坏是O(n^2),平均时间复杂度为O(nlogn),最好情况的时间复杂度为O(nlogn)。
排序思想
快排需要将序列变成两个部分,就是「序列左边全部小于一个数」,「序列右面全部大于一个数」,然后利用递归的思想再将左序列当成一个完整的序列再进行排序,同样把序列的右侧也当成一个完整的序列进行排序。
其中这个数在这个序列中是可以随机取的,可以取最左边,可以取最右边,当然也可以取随机数。但是「通常」不优化情况我们取最左边的那个数。
排序案例
例如2 5 3 1 4排序过程如下
第一次排序,选定第一个数字2作为比较分为两部分,[1] 2 [5 3 4]
第二次排序,1就剩一个不在处理,处理5 3 4,取5作为比较,[3 4] 5
至此完成排序,1 2 3 4 5
代码实现
/**
* 快速排序
*
* @param array 要排序的数组
* @param left 第一个元素下标
* @param right 最后一个元素下标
*/
private static void quickSort(int[] array, int left, int right) {
int low = left;
int high = right;
if (low > high) {
return;
}
// 取数组第一个数k作为衡量标准
int k = array[low];
while (low < high) {
// 右侧找到第一个小于k的停止
while (low < high && array[high] >= k) {
high--;
}
// 找到第一个比k小的数,放在low的位置
array[low] = array[high];
//找到第一个大于k的值停止
while (low < high && array[low] <= k) {
low++;
}
array[high] = array[low];
}
//赋值,然后左右递归
array[low] = k;
quickSort(array, left, low - 1);
quickSort(array, low + 1, right);
System.out.println("快速排序:" + JSON.toJSONString(array));
}
2.3 直接插入排序
直接插入排序在所有排序算法中的是最简单排序方式之一。和我们上学时候 从前往后、按高矮顺序排序,那么一堆高低无序的人群中,从第一个开始,如果前面有比自己高的,就直接插入到合适的位置。「一直到队伍的最后一个完成插入」整个队列才能满足有序。
直接插入排序遍历比较时间复杂度是每次O(n),交换的时间复杂度每次也是O(n),那么n次总共的时间复杂度就是O(n2)。有人会问折半(二分)插入能否优化成O(nlogn),答案是不能的。因为二分只能减少查找复杂度每次为O(logn),而插入的时间复杂度每次为O(n)级别,这样总的时间复杂度级别还是O(n2).
排序思想
选取当前位置(当前位置前面已经有序) 目标就是将当前位置数据插入到前面合适位置。
向前枚举或者二分查找,找到待插入的位置。
移动数组,赋值交换,达到插入效果。
排序案例
例如2 5 3 1 4排序过程如下
第一趟排序:2 5 3 1 4
第二趟排序:2 5 3 1 4
第三趟排序:2 5 3 1 4
代码实现
/**
* 直接插入排序
*
* @param array 要排序的数组
*/
private static void insertSort(int[] array) {
int variable;
for (int i = 0; i < array.length; i++) {
variable = array[i];
for (int j = i - 1; j >= 0; j--) {
if (array[j] > variable) {
array[j + 1] = array[j];
array[j] = variable;
} else {
break;
}
}
}
System.out.println("直接插入排序:" + JSON.toJSONString(array));
}
2.4 希尔排序
直接插入排序因为是O(n^2),在数据量很大或者数据移动位次太多会导致效率太低。很多排序都会想办法拆分序列,然后组合,希尔排序就是以一种特殊的方式进行预处理,考虑到了「数据量和有序性」两个方面纬度来设计算法。使得序列前后之间小的尽量在前面,大的尽量在后面,进行若干次的分组别计算,最后一组即是一趟完整的直接插入排序。
排序思想
对于一个长串,希尔首先将序列分割(非线性分割)而是「按照某个数模」(取余这个类似报数1、2、3、4。1、2、3、4)这样形式上在一组的分割先「各组分别进行直接插入排序」,这样「很小的数在后面」可以通过「较少的次数移动到相对靠前」的位置。然后慢慢合并变长,再稍稍移动。
因为每次这样插入都会使得序列变得更加有序,稍微有序序列执行直接插入排序成本并不高。所以这样能够在合并到最终的时候基本小的在前,大的在后,代价越来越小。这样希尔排序相比插入排序还是能节省不少时间的。
排序案例
代码实现
/**
* 希尔排序
*
* @param array 要排序的数组
*/
private static void hillSort(int[] array) {
int d = array.length;
//临时变量
int variable;
//共分成d组
for (; d >= 1; d /= 2) {
//到那个元素就看这个元素在的那个组即可
for (int i = d; i < array.length; i++) {
variable = array[i];
for (int j = i - d; j >= 0; j -= d) {
if (array[j] > variable) {
array[j + d] = array[j];
array[j] = variable;
} else {
break;
}
}
}
}
System.out.println("希尔排序:" + JSON.toJSONString(array));
}
2.5 简单选择排序
简单选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到「已排序序列的末尾」。以此类推,直到所有元素均排序完毕。
排序思想
排序案例
代码实现
/**
* 简单选择排序
*
* @param array 要排序的数组
*/
private static void selectSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
int min = i; // 最小位置
for (int j = i + 1; j < array.length; j++) {
if (array[j] < array[min]) {
min = j; // 更换最小位置
}
}
if (min != i) {
swap(array, i, min); // 与第i个位置进行交换
}
}
System.out.println("简单选择排序:" + JSON.toJSONString(array));
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
2.6 堆排序
对于堆排序,首先是建立在堆的基础上,堆是一棵完全二叉树,还要先认识下大根堆和小根堆,完全二叉树中所有节点均大于(或小于)它的孩子节点,所以这里就分为两种情况
如果所有节点「大于」孩子节点值,那么这个堆叫做「大根堆」,堆的最大值在根节点。
如果所有节点「小于」孩子节点值,那么这个堆叫做「小根堆」,堆的最小值在根节点。
排序思想
排序案例
代码实现
static void swap(int arr[],int m,int n)
{
int team=arr[m];
arr[m]=arr[n];
arr[n]=team;
}
//下移交换 把当前节点有效变换成一个堆(小根)
static void shiftDown(int arr[],int index,int len)//0 号位置不用
{
int leftchild=index*2+1;//左孩子
int rightchild=index*2+2;//右孩子
if(leftchild>=len)
return;
else if(rightchild<len&&arr[rightchild]<arr[index]&&arr[rightchild]<arr[leftchild])//右孩子在范围内并且应该交换
{
swap(arr, index, rightchild);//交换节点值
shiftDown(arr, rightchild, len);//可能会对孩子节点的堆有影响,向下重构
}
else if(arr[leftchild]<arr[index])//交换左孩子
{
swap(arr, index, leftchild);
shiftDown(arr, leftchild, len);
}
}
//将数组创建成堆
static void creatHeap(int arr[])
{
for(int i=arr.length/2;i>=0;i--)
{
shiftDown(arr, i,arr.length);
}
}
static void heapSort(int arr[])
{
System.out.println("原始数组为 :"+Arrays.toString(arr));
int val[]=new int[arr.length]; //临时储存结果
//step1建堆
creatHeap(arr);
System.out.println("建堆后的序列为 :"+Arrays.toString(arr));
//step2 进行n次取值建堆,每次取堆顶元素放到val数组中,最终结果即为一个递增排序的序列
for(int i=0;i<arr.length;i++)
{
val[i]=arr[0];//将堆顶放入结果中
arr[0]=arr[arr.length-1-i];//删除堆顶元素,将末尾元素放到堆顶
shiftDown(arr, 0, arr.length-i);//将这个堆调整为合法的小根堆,注意(逻辑上的)长度有变化
}
//数值克隆复制
for(int i=0;i<arr.length;i++)
{
arr[i]=val[i];
}
System.out.println("堆排序后的序列为:"+Arrays.toString(arr));
}
2.7 归并排序
在归并类排序一般只讲归并排序,但是归并排序也分二路归并、多路归并,这里就讲较多的二路归并排序,且用递归方式实现。
排序思想
归并和快排都是「基于分治算法」的,分治算法其实应用挺多的,很多分治会用到递归,但事实上「分治和递归是两把事」。分治就是分而治之,可以采用递归实现,也可以自己遍历实现非递归方式。而归并排序就是先将问题分解成代价较小的子问题,子问题再采取代价较小的合并方式完成一个排序。
至于归并的思想是这样的:
第一次:整串先进行划分成一个一个单独,第一次是将序列中(1 2 3 4 5 6—)两两归并成有序,归并完(xx xx xx xx----)这样局部有序的序列。
第二次就是两两归并成若干四个(1 2 3 4 5 6 7 8 ----)「每个小局部是有序的」。
就这样一直到最后这个串串只剩一个,然而这个耗费的总次数logn。每次操作的时间复杂的又是O(n)。所以总共的时间复杂度为O(nlogn).
排序案例
代码实现
private static void mergesort(int[] array, int left, int right) {
int mid=(left+right)/2;
if(left<right)
{
mergesort(array, left, mid);
mergesort(array, mid+1, right);
merge(array, left,mid, right);
}
}
private static void merge(int[] array, int l, int mid, int r) {
int lindex=l;int rindex=mid+1;
int team[]=new int[r-l+1];
int teamindex=0;
while (lindex<=mid&&rindex<=r) {//先左右比较合并
if(array[lindex]<=array[rindex])
{
team[teamindex++]=array[lindex++];
}
else {
team[teamindex++]=array[rindex++];
}
}
while(lindex<=mid)//当一个越界后剩余按序列添加即可
{
team[teamindex++]=array[lindex++];
}
while(rindex<=r)
{
team[teamindex++]=array[rindex++];
}
for(int i=0;i<teamindex;i++)
{
array[l+i]=team[i];
}
}
2.8 桶排序
桶排序是一种用空间换取时间的排序,桶排序重要的是它的思想,而不是具体实现,时间复杂度最好可能是线性O(n),桶排序不是基于比较的排序而是一种分配式的。桶排序从字面的意思上看:
桶:若干个桶,说明此类排序将数据放入若干个桶中。
桶:每个桶有容量,桶是有一定容积的容器,所以每个桶中可能有多个元素。
桶:从整体来看,整个排序更希望桶能够更匀称,即既不溢出(太多)又不太少。
排序思想
桶排序的思想为:「将待排序的序列分到若干个桶中,每个桶内的元素再进行个别排序。」 当然桶排序选择的方案跟具体的数据有关系,桶排序是一个比较广泛的概念,并且计数排序是一种特殊的桶排序,基数排序也是建立在桶排序的基础上。在数据分布均匀且每个桶元素趋近一个时间复杂度能达到O(n),但是如果数据范围较大且相对集中就不太适合使用桶排序。
排序案例
代码实现
/**
* 桶排序
*/
private static void bucketSort() {
int[] a = {1, 8, 7, 44, 42, 46, 38, 34, 33, 17, 15, 16, 27, 28, 24};
List[] buckets = new ArrayList[5];
//初始化
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new ArrayList<Integer>();
}
//将待排序序列放入对应桶中
for (int i = 0; i < a.length; i++) {
int index = a[i] / 10;//对应的桶号
buckets[index].add(a[i]);
}
//每个桶内进行排序(使用系统自带快排)
for (int i = 0; i < buckets.length; i++) {
buckets[i].sort(null);
for (int j = 0; j < buckets[i].size(); j++)//顺便打印输出
{
System.out.print(buckets[i].get(j) + " ");
}
}
}
2.9 计数排序
计数排序是一种特殊的桶排序,每个桶的大小为1,每个桶不在用List表示,而通常用一个值用来计数。
在「设计具体算法的时候」,先找到最小值min,再找最大值max。然后创建这个区间大小的数组,从min的位置开始计数,这样就可以最大程度的压缩空间,提高空间的使用效率。
排序思想
排序案例
代码实现
/**
* 计数排序
*/
private static void countSort(int[] a) {
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
//找到max和min
for (int i = 0; i < a.length; i++) {
if (a[i] < min) {
min = a[i];
}
if (a[i] > max) {
max = a[i];
}
}
int[] count = new int[max - min + 1];//对元素进行计数
for (int i = 0; i < a.length; i++) {
count[a[i] - min]++;
}
//排序取值
int index = 0;
for (int i = 0; i < count.length; i++) {
while (count[i]-- > 0) {
a[index++] = i + min;//有min才是真正值
}
}
}
2.10 基数排序
基数排序是一种很容易理解但是比较难实现(优化)的算法。基数排序也称为卡片排序,基数排序的原理就是多次利用计数排序(计数排序是一种特殊的桶排序),但是和前面的普通桶排序和计数排序有所区别的是,「基数排序并不是将一个整体分配到一个桶中」,而是将自身拆分成一个个组成的元素,每个元素分别顺序分配放入桶中、顺序收集,当从前往后或者从后往前每个位置都进行过这样顺序的分配、收集后,就获得了一个有序的数列。
排序思想
排序案例
代码实现
/**
* 基数排序
*/
private static void radixSort(int[] arr) {
{
ArrayList[] bucket = new ArrayList[10];
for (int i = 0; i < 10; i++) {
bucket[i] = new ArrayList<>();
}
//找到最大值
int max = 0;//假设都是正数
for (int i = 0; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
int divideNum = 1;//1 10 100 100……用来求对应位的数字
while (max > 0) {//max 和num 控制
for (int num : arr) {
bucket[(num / divideNum) % 10].add(num);//分配 将对应位置的数字放到对应bucket中
}
divideNum *= 10;
max /= 10;
int idx = 0;
//收集 重新捡起数据
for (List<Integer> list : bucket) {
for (int num : list) {
arr[idx++] = num;
}
list.clear();//收集完需要清空留下次继续使用
}
}
}
}