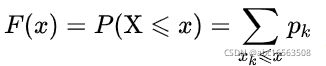NDT（正态分布变换）算法学习
NDT（正态分布变换）算法学习
近期阅读NICP. Dense Normal Based Point Cloud Registration论文，其中的点云配准算法：ICP、NDT、GICP、NICP较感兴趣，小白进行学习。
推荐相关视频或文章：https://www.bilibili.com/video/BV1NK411T71n（NDT算法）
概率分布函数、概率密度函数 - 知乎（概率分布函数、概率密度函数）
如何直观地理解「协方差矩阵」？ - 知乎（协方差矩阵）
引入：三维空间中一个点有xyz三个数据，xyz数据使用双精度值来描绘（双精度值：比如一个数据是八个比特，三个xyz就是3*8=24bit，几万个点的话数据量很大）。
NDT（正态分布变换）算法：可以保证一个方格里就用一个概率分布函数进行描绘（概率分布函数主要因素是协方差矩阵、平均值 [为什么使用协方差矩阵和平均值？文章结尾的名词解释我觉得可以挺好的理解]）。此算法可以将离散的点变连续函数描绘，并场景信息压缩（压缩方法：放在一个方格中进行协方差矩阵、平均值的计算）
上述：双精度、概率密度函数、协方差名词解释在文章结尾，图片引用的是视频中的。
二维场景：
二维点是稀疏的，有的方块里密集有的方块里稀疏（求导求拐点是不适用的）
上图中密集方格中的点如何将其变成一个连续的函数去描绘？
答：用概率分布函数进行描绘，这个方格里出现的点云概率是多少，红色和黄色的部分就是通过求解点云的协方差矩阵、平均值得到。（这些点离其平均值越远，他的协方差矩阵在这个方向上的特征向量的特征值越大），总的来说可以描绘这部分点云的朝向、平整度。
三维场景：
有三个特征向量，可以形象的有三个箭头，如果一个箭头比较长的话。会将这团点云的形状拉长。同样也是在一个方格中，与上述二维场景的解释相呼应。
算法优化：如果一个方格一个方格分的话，方格和方格之间会有抖动（激变），会导致之后配准有误差。1、一个方格一个方格之间平移半个方格，这中间会有重叠区域，有重叠区域的拼出来的概率分布函数会有平滑的效果，对配准有很大帮助。2、八叉树的优化方法：在点云稀疏的部分用大方格，点云密集的部分用小方格对数据量进一步压缩，运算压力进一步释放。
视频中还有闭环检测，暂时没有详细学习，后续学习加入。
名词解释：（开头的链接感兴趣的可以详细看看，真心写的挺好）
双精度值：与单精度的区别在于小数点后面保留位数不一致（即精度）。浮点数
float的精度是6位有效数字，取值范围是10的-38次方到10的38次方，float占用4字节空间
double的精度是15位有效数字，取值范围是10的-308次方到10的308次方,double占用8字节空间。
概率分布函数：又称为离散型随机变量的分布函数，通过下式得到是X≤x的诸值xk的概率之和，又称之为积累概率函数。
概率函数是用函数的形式来表达概率，概率函数一次只能一个取值的概率。
概率分布侧重点在分布，离散型随机变量的值分布和概率分布。
概率密度函数：连续型随机变量的概率函数，首先连续型随机变量的数值是连续的。其次，概率密度函数其实是一个定积分函数，定积分在数学一般用来求面积。然后记住概率密度函数值就是概率在该点的变化率
方差：方差是标准差的平方，标准差的意义是数据集中各个点到均值点距离的平均值，反应的是数据的离散程度。
协方差：标准差和方差是描述一维数据的，当存在多维数据的时候，需要知道每个维数的变量中间是否存在关联。协方差是衡量多维数据中变量之间相关性的统计量。比如一个人身高和体重的关系，两变量之间协方差为正值，则两个变量之间存在正相关。
协方差矩阵：当变量多了，超过两个变量，就用协方差矩阵衡量多变量之间的相关性。由方差和协方差两部分组成，方差构成了对角线上的元素，协方差构成了非对角线上的元素。协方差矩阵的特征向量控制旋转，特征值控制尺度，均值向量控制位置