深度推荐模型 -NFM

NFM

参考 推荐系统遇上深度学习(七)–NFM模型理论和实践

提出背景 & 与其他模型的关系

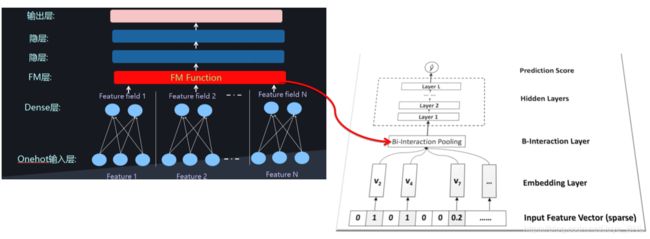
NFM这个模型是在FM的基础上提出的，是为了改进FM模型只能表达特征之间两两组合之间的关系，无法建模两个特征之间深层次的关系或者说多个特征之间的交互关系，同时为了建模更高阶的特征而提出的。NFM是串行结构中一种较为简单的网络模型。

NFM(Neural Factorization Machines)是2017年由新加坡国立大学的何向南教授等人在SIGIR会议上提出的一个模型，**传统的FM模型仅局限于线性表达和二阶交互， 无法胜任生活中各种具有复杂结构和规律性的真实数据。**针对FM的这点不足，作者提出了一种将FM融合进DNN的策略，通过引进了一个特征交叉池化层的结构，使得FM与DNN进行了完美衔接，这样就组合了FM的建模低阶特征交互能力和DNN学习高阶特征交互和非线性的能力，形成了深度学习时代的神经FM模型(NFM)。

结构	描述	常见模型
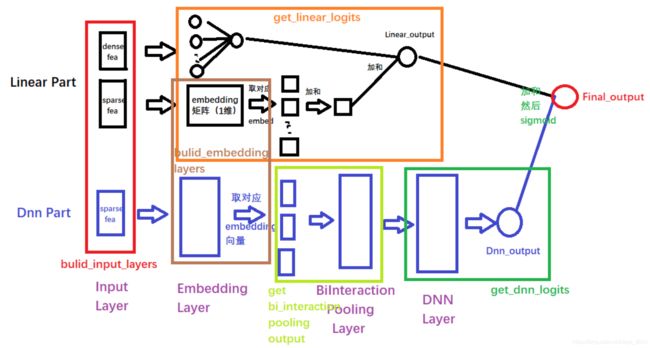
并行结构	FM部分和DNN部分分开计算，只在输出层进行一次融合得到结果	DeepFM，DCN，Wide&Deep
串行结构	将FM的一次项和二次项结果(或其中之一)作为DNN部分的输入，经DNN得到最终结果	PNN,NFM,AFM

FM回顾

FM模型用n个隐变量来刻画特征之间的交互关系。这里要强调的一点是，n是特征的总数，是one-hot展开之后的，比如有三组特征，两个连续特征，一个离散特征有5个取值，那么n=7而不是n=3.

$\hat{y}(X)={\omega }_0+{\sum }_{i=1}^n{\omega }_i{x}_i+{\sum }_{i=1}^{n-1}{\sum }_{j=i+1}^n<v_i,v_j>x_i{x}_j$
$<v_i,v_j>={\sum }_{f=1}^k{v}_{i,f}\cdot v_{j,f}$

FM的化简公式也很重要：
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \sum_{i=1}^{n-…

• $v_{i,f}$ 是一个具体的值；
• 第1个等号：对称矩阵 $W$ 对角线上半部分；
• 第2个等号：把向量内积 $v_i$,$v_j$ 展开成累加和的形式；
• 第3个等号：提出公共部分；
• 第4个等号： $i$ 和 $j$ 相当于是一样的，表示成平方过程。
  不考虑最外层的求和时，我们可以得到一个K维的向量。

NFM公式

${\hat{y}}_{NFM}(\mathbf{x})=w_0+{\sum }_{i=1}^n{w}_i{x}_i+f(\mathbf{x})$

对比FM，发现变化的是第三项，前两项还是原来的。因为FM的一个问题，就是只能到二阶交叉，且是线性模型。作者在这里改进的思路就是用一个表达能力更强的函数来替代原FM中二阶隐向量内积的部分。这个能力够强的函数就是神经网络，因为神经网络理论上可以拟合任何复杂的函数。

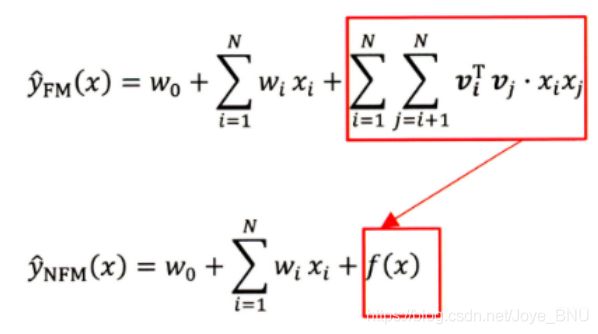
NFM网络总体结构

这个结构和PNN非常像，只不过那里是一个product_layer， 而这里换成了Bi-Interaction Pooling了， 这个也是NFM的核心结构了。注意，这里忽略了一阶部分，只可视化出来了$f(x)$.

网络各层的详细解释

Input层和Embedding层

输入层的特征， 文章指定了稀疏离散特征居多， 这种特征我们也知道一般是先one-hot, 然后会通过embedding，处理成稠密低维的。 所以这两层还是和之前一样，假设${\mathbf{v}}_{\mathbf{i}}\in {\mathbb{R}}^k$为第$i$个特征的embedding向量， 那么${\mathcal{V}}_x=\left\{x_1{\mathbf{v}}_1,\dots ,x_n{\mathbf{v}}_n\right\}$表示的下一层的输入特征。这里带上了$x_i$是因为很多$x_i$转成了One-hot之后，出现很多为0的， 这里的$\{x_i{v}_i\}$是$x_i$不等于0的那些特征向量。

Bi-Interaction Pooling layer

在Embedding层和神经网络之间加入了特征交叉池化层是本网络的核心创新了，**正是因为这个结构，实现了FM与DNN的无缝连接，组成了一个大的端到端网络，且能够正常的反向传播。**假设${\mathcal{V}}_x$是所有特征embedding的集合， 那么在特征交叉池化层的操作：
$f_{BI}\left({\mathcal{V}}_x\right)={\sum }_{i=1}^n{\sum }_{j=i+1}^n{x}_i{\mathbf{v}}_i\odot x_j{\mathbf{v}}_j$
$\odot$表示两个向量的元素积操作，即两个向量对应维度相乘得到的元素积向量（可不是点乘呀），其中第$k$维的操作：
${\left(v_i\odot v_j\right)}_k={\mathbf{v}}_{ik}{\mathbf{v}}_{jk}$

这便定义了在embedding空间特征的二阶交互，这个不仔细看会和感觉FM的最后一项很像，但是不一样，要注意这个地方不是两个隐向量的内积，而是元素积，也就是这一个交叉完了之后k个维度不求和，最后会得到一个$k$维向量，而FM那里内积的话最后得到一个数，在进行两两Embedding元素积之后，对交叉特征向量取和，得到该层的输出向量，很显然，输出是一个$k$维的向量。

加入特征池化层之后，把二阶交互的信息合并，且上面接了一个DNN网络，这样就能够增强FM的表达能力了，因为FM只能到二阶，而这里的DNN可以进行多阶且非线性，只要FM把二阶的学习好了，DNN学习来会更加容易。作者在论文中也说明了这一点，且通过后面的实验证实了这个观点。

如果不加DNN，NFM就退化成了FM（还是有区别的吧，毕竟FM特征交叉时使用的是内积），所以改进的关键就在于加了一个BI-interaction Pooling层，组合了一下二阶交叉的信息，然后又给了DNN进行高阶交叉的学习，成了一种“加强版”的FM。

Bi-Interaction层不需要额外的模型学习参数，更重要的是它在一个线性的时间内完成计算，和FM一致的，即时间复杂度为$O\left(k{N}_x\right)$，$N_x$为embedding向量的数量。参考FM，可以将上式转化为：
$$f_{BI}\left({\mathcal{V}}_x\right)=\frac{1}{2}\left[{\left(\sum _{i=1}^n{x}_i{\mathbf{v}}_i\right)}^2-\sum _{i=1}^n{\left(x_i{\mathbf{v}}_i\right)}^2\right]$$
后面代码复现NFM就是用的这个公式直接计算。

隐藏层

这一层就是全连接的神经网络， DNN在进行特征的高层非线性交互上有着天然的学习优势，公式如下：
$$\begin{array}{rl}{\mathbf{z}}_1=& {\sigma }_1\left({\mathbf{W}}_1{f}_{BI}\left({\mathcal{V}}_x\right)+{\mathbf{b}}_1\right)\\ {\mathbf{z}}_2=& {\sigma }_2\left({\mathbf{W}}_2{\mathbf{z}}_1+{\mathbf{b}}_2\right)\\ \dots \dots & \\ {\mathbf{z}}_L=& {\sigma }_L\left({\mathbf{W}}_L{\mathbf{z}}_{L-1}+{\mathbf{b}}_L\right)\end{array}$$
这里的${\sigma }_i$是第$i$层的激活函数，可不要理解成sigmoid激活函数。

预测层

$f(\mathbf{x})={\mathbf{h}}^T{\mathbf{z}}_L$
注意由于这里是回归问题，没有加sigmoid激活。

小结

NFM模型的前向传播过程总结如下：
$$\begin{array}{rl}{\hat{y}}_{NFM}(\mathbf{x})& =w_0+\sum _{i=1}^n{w}_i{x}_i\\ & +{\mathbf{h}}^T{\sigma }_L\left({\mathbf{W}}_L\left(\dots {\sigma }_1\left({\mathbf{W}}_1{f}_{BI}\left({\mathcal{V}}_x\right)+{\mathbf{b}}_1\right)\dots \right)+{\mathbf{b}}_L\right)\end{array}$$

这就是NFM模型的全貌，NFM相比较于其他模型的核心创新点是特征交叉池化层，基于它，实现了FM和DNN的无缝连接，使得DNN可以在底层就学习到包含更多信息的组合特征，这时候，就会减少DNN的很多负担，只需要很少的隐藏层就可以学习到高阶特征信息。NFM相比之前的DNN， 模型结构更浅，更简单，但是性能更好，训练和调参更容易。集合FM二阶交叉线性和DNN高阶交叉非线性的优势，非常适合处理稀疏数据的场景任务。在对NFM的真实训练过程中，也会用到像Dropout和BatchNormalization这样的技术来缓解过拟合和在过大的改变数据分布。

总体的结构图如下：