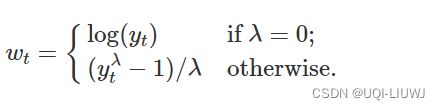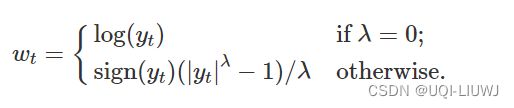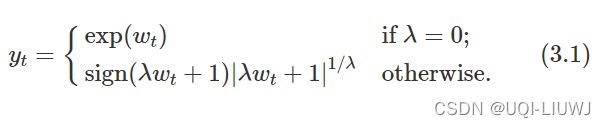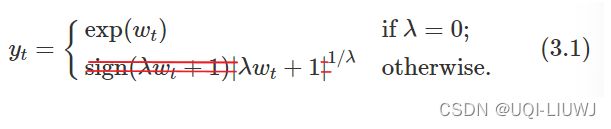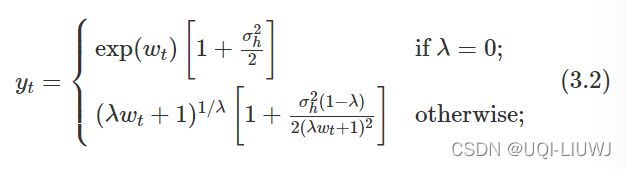机器学习笔记 时间序列预测（基本数据处理，Box-Cox）

  数据调整

         调整历史数据通常会导致更简单的预测任务。

        在这里，我们处理四种调整：日历调整、人口调整、通货膨胀调整和数学变换。

        这些调整和转换的目的是通过消除已知的变化源或通过使整个数据集的模式更加一致来简化历史数据中的模式。 更简单的模式通常会导致更准确的预测。

1 日历调整

        在季节性数据中看到的一些变化可能是由于简单的日历效应。 在这种情况下，如果在拟合预测模型之前消除变化，通常更容易。

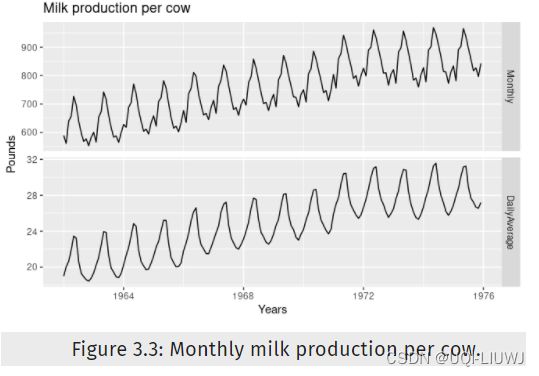
        例如，如果您正在研究农场的每月牛奶产量，除了全年的季节性变化外，由于每个月的天数不同，月份之间也会存在差异。

        

         请注意，与每月总产量图（上图）相比，平均日产量图（下图）中的季节性模式要简单得多。 通过查看平均每日产量而不是每月总产量，我们有效地消除了由于月份长度不同而导致的变化。 更简单的模式通常更容易建模并导致更准确的预测。

2 人口调整

        任何受人口变化影响的数据都可以调整为人均数据。 也就是说，考虑每人（或每千人或每百万人）的数据而不是总数。

         例如，如果您正在研究某个特定地区的医院床位数量随时间的变化，如果您通过考虑每千人的床位数量来消除人口变化的影响，那么结果会更容易解释。 然后你可以看到床的数量是否真的增加了，或者增加是否完全是由于人口的增加。 总床位数可能增加，但每千人床位数减少。 当人口增长速度快于病床数量时，就会出现这种情况。

         对于大多数受人口变化影响的数据，最好使用人均数据而不是总数。

3 通货膨胀调整

        受货币价值影响的数据最好在拟合模型之前进行调整。

        例如，由于通货膨胀，过去几十年来新房的平均成本将会增加。 今年 20 万美元的房子和 20 年前 20 万美元的房子不同。 出于这个原因，通常会调整金融时间序列，以便所有值都以特定年份的美元值表示。 例如，房价数据可能以 2000 年美元表示。

        为了进行这些调整，使用了价格指数。 如果 zt 表示价格指数，yt 表示 t 年的原始房价，则 xt=yt/zt ∗z2000 给出 2000 年美元价值的调整后房价。 价格指数通常由政府机构构建。 对于消费品，常见的价格指数是消费者价格指数（或 CPI）。

4 数学调整

        如果数据显示随序列水平增加或减少的变化，则数据转换可能很有用。

         例如，对数变换通常很有用。 如果我们将原始观测值表示为 y1,...,yT 并将转换后的观测值表示为 w1,...,wT ，那么 wt=log(yt) 。

        对数很有用，因为它们是可解释的：对数值的变化是原始尺度上的相对（或百分比）变化。 因此，如果使用以 10 为底的对数，则对数刻度增加 1 对应于原始刻度的 10 倍增。

        对数转换的另一个有用特性是它们将预测限制为在原始规模上保持正数。

         有时也使用其他转换（尽管它们不是那么可解释）。 例如，可以使用平方根和立方根。 这些被称为幂变换，因为它们可以写成形式

4.1Box-Cox 变换族 

         一个有用的变换族，包括对数和幂变换，是 Box-Cox 变换族，它取决于参数 λ，定义如下：

        

         Box-Cox 变换中的对数始终是自然对数（即以 e 为底）。 因此，如果 λ=0 ，则使用自然对数，但如果 λ≠0 ，则使用幂变换，然后进行一些简单的缩放。

        如果 λ=1 ，则 wt=yt−1 ，因此变换后的数据向下移动，但时间序列的形状没有变化。 但对于 λ 的所有其他值，时间序列将改变形状。

        如何选择λ呢？Box-Cox希望转换后的数据服从线性，即 【换句话说，是把一组数据变得正态化】

用图像来表示的话（使用Box-Cox转换的益处 - 知乎 (zhihu.com)

Box-Cox可以是做这样的事

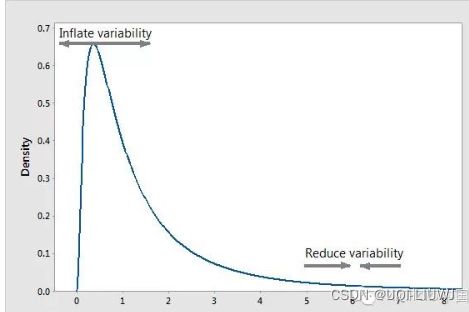
原来（Y）的数据分布

 那么我们希望0~1部分分布区域变大，1~8部分分布区域变小

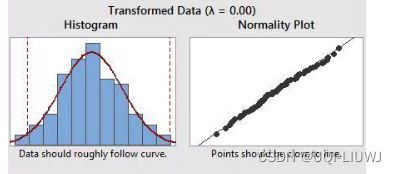
下面是Box-Cox 变换之后的分布

 可以发现不对称分布的数据已经转换成了一个对称的正态分布

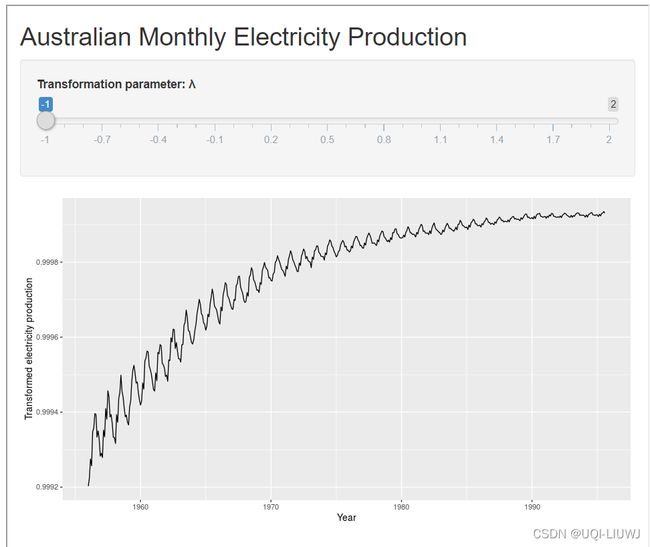
4.1.1 不同λ下Box-Cox的曲线

比如这是λ=1的时候的曲线：

λ=-1时候的曲线

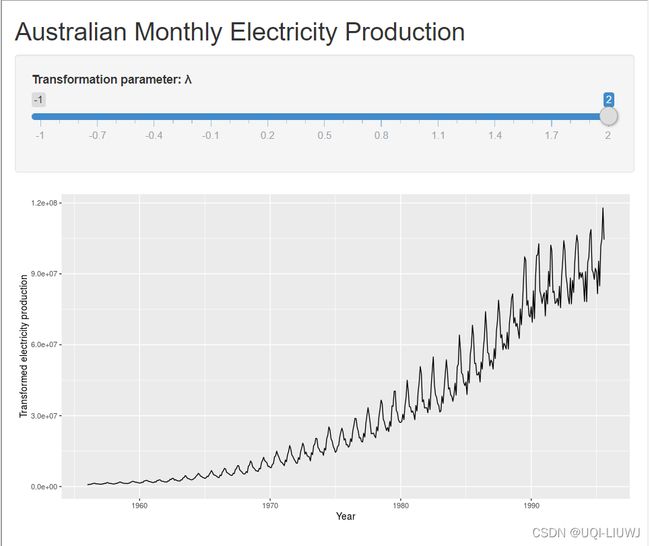
 λ=2时候的曲线

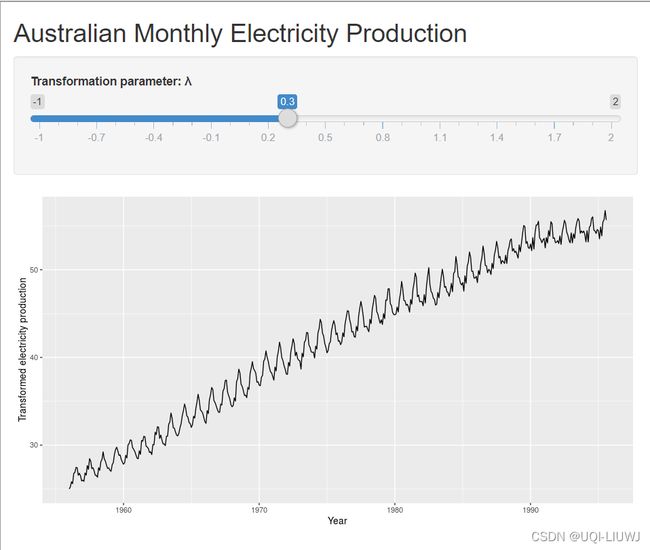
         一个好的 λ 值可以使整个系列的季节变化的大小大致相同，因为这使得预测模型更简单。 在这种情况下，λ=0.30 效果很好，尽管 0 到 0.5 之间的任何 λ 值都会给出类似的结果。

        

 4.1.2 R语言实现

library(BoxCox)

y<-ts(c(5,3,3.1,3.2,3.3,3.4,3.5,3.3,3.2,4,4.1,4.2,
         6,4,4.1,4.2,4.3,4.4,4.5,4.6,4.7,4.8,4.9,5,
         10,9,8,8.5,8.4,8.5,8.6,8.7,8.8,8.9,9,9.5),
       start = 2020,
       frequency = 12)

b=boxcox(y~.,data=y)
l=which(b$y==max(b$y))

l  #75

b$x[l]  #0.989899

也就是这里0.989899就是最佳的λ，也就是'b=boxcox(y~.,data=y)'输出的图的最高点

  4.1.3 允许负数的Box-Cox变换（及其逆变换）

       BoxCox() 命令实际上实现了对 Box-Cox 变换的轻微修改，当 λ>0 时允许 yt 为负值：

        

        正数部分的yt，和原来的Box-Cox变换是一样的

         选择转换后，我们需要预测转换后的数据。 然后，我们需要逆向变换（或反向变换）以获得原始尺度的预测。 反向 Box-Cox 变换由下式给出      

                 

 5 偏差调整

        使用诸如 Box-Cox 变换之类的数学变换的一个问题是，反向变换的点预测将不是预测分布的平均值。 事实上，它通常是预测分布的中位数（假设变换空间上的分布是对称的）。

 

        出于许多目的，这是可以接受的，但有时需要平均预测。 例如，您可能希望将各个地区的销售预测相加，形成整个国家的预测。 但是中位数不加起来，而平均值加起来。

以不考虑负数的Box-Cox为例：

它的逆变换为

 而逆变换的均值为：

 其中 是 h 步预测方差。 预测方差越大，均值和中位数之间的差异越大。         

（3.1改）给出的简单反向变换预测与（3.2）给出的平均值之间的差异称为偏差。 当我们使用平均值而不是中位数时，我们说点预测已经过偏差调整 bias-adjusted。

5.1 R语言实现

        要了解这种偏差调整有多大差异，请考虑以下示例，我们使用带有对数变换 (λ=0) 的漂移方法预测鸡蛋的年平均价格。 在这种情况下，对数转换有助于确保预测和预测区间保持正数。

 漂移方法见：机器学习笔记 时间序列预测（最基本的方法【benchmark】）_UQI-LIUWJ的博客-CSDN博客

library(forecast)

fc<-rwf(y,drift=TRUE,h=50)

fc1<-rwf(y,drift=TRUE,h=50,biasadj = TRUE)

autoplot(y)+
 autolayer(fc,series='simple back transformation')+
 autolayer(fc1,series = 'bias adjusted',PI=FALSE)

参考内容 使用Box-Cox转换的益处 - 知乎 (zhihu.com)