研究生工作周报

学习目标（第二周）：

吴恩达教授深度学习课程《神经网络与深度学习》

• 神经网络基础

《机器学习实战》

• 对十大机器学习算法初步了解，会调用scikit learn和它的contrib库，熟练之后尝试复现。
• 结合视频课程以及之前的基础，计划重点看监督学习算法。逻辑回归，决策树，朴素贝叶斯，支持向量机和降维方法PCA
  
  

学习内容：

视频课程内容

1. 二元分类 (Binary Classification)
2. Logistic 回归 (Logistic Regression)
3. 梯度下降法 (Gradient Descent)
4. 向量化 (Vectorization)
5. 向量化 Logistic 回归的梯度输出 (Vectorizing Logistic Regression’s Gradient Computation)
6. 建立一个【猫猫识别】神经网络

《机器学习实战》前六章

熟悉算法原理，跑示例代码帮助理解

---

学习时间：

• 5.15-5.21

---

学习产出：

• 完成Week2 神经网络基础课后习题以及编程作业
• CSDN 博客 1 篇
  
  

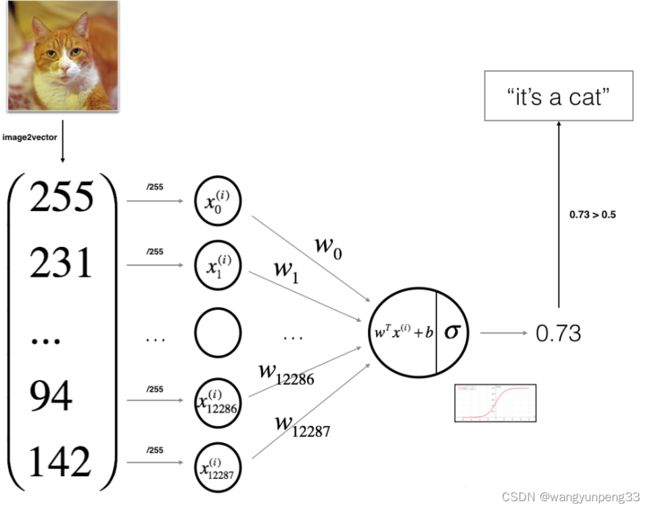
二元分类

 在二分类问题中，我们的目标就是习得一个分类器，它以图片的特征向量x作为输入，然后预测输出 y 结果为1还是0。

逻辑回归

逻辑回归适用于解决二分类问题，给出输入 $x$ 以及参数 $w$ 和 $b$ 之后，产生输出预测值
$$\hat{y}=\sigma (w^{T}x+b)$$
$$\sigma (z)=\frac{1}{1+e^{-z}}$$
损失函数(误差函数)$L$：

$$L(\hat{y},y)=-y\log (\hat{y})-(1-y)\log (1-\hat{y})$$
损失函数是在单个训练样本中定义的，它衡量的是算法在单个训练样本中的表现，为了衡量算法在全部训练样本上的表现如何，我们需要定义一个算法的代价函数，算法的代价函数是对 m 个样本的损失函数求和然后除以 m :

$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})=\frac{1}{m}\sum _{i=1}^m(-y^{(i)}\log {\hat{y}}^{(i)}-(1-y^{(i)})\log (1-{\hat{y}}^{(i)}))$$
所以在训练逻辑回归模型时候，我们需要找到合适的 $w$ 和 $b$ ，来让代价函数 $J$ 的总代价降到最低。

梯度下降法 (Gradient Descent)

在测试集上，通过最小化代价函数（成本函数） $J(w,b)$来训练的参数 $w$和$b$

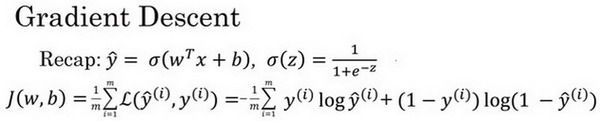
朝最陡的下坡方向走一步，不断地迭代，直到走到全局最优解或者接近全局最优解的地方。

α 表示学习率（learning rate），用来控制步长（step）
α越小，代价函数J收敛的越慢，而α过大又会导致J在最小值附近震荡

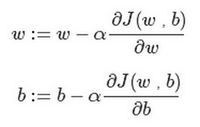
例如对于有两个特征$w1$ $w2$的m个样本的逻辑回归梯度下降算法

代码流程

J=0;dw1=0;dw2=0;db=0;
for i = 1 to m
    z(i) = wx(i)+b;
    a(i) = sigmoid(z(i));
    J += -[y(i)log(a(i))+(1-y(i)）log(1-a(i));
    dz(i) = a(i)-y(i);
    dw1 += x1(i)dz(i);
    dw2 += x2(i)dz(i);
    db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db

向量化 (Vectorization)

在应用深度学习算法时，显式地使用for循环使算法很低效，引入向量化技术,它可以允许你的代码摆脱这些显式的for循环。
在逻辑回归中你需要去计算 $z=w^{T}x+b$

x
z=0
for i in range(n_x)
    z+=w[i]*x[i]
z+=b

向量化实现z=np.dot(w,x)+b

理解Python的广播（broadcasting）功能以及在Python-numpy中构造向量
记录两道有意思的题

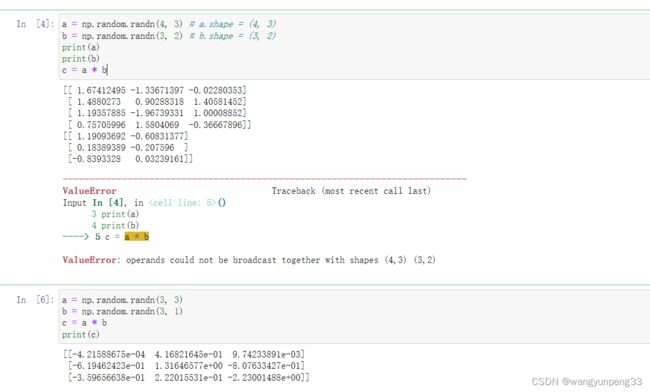
Q1:考虑以下两个随机数组a和b：

a = np.random.randn(4, 3) # a.shape = (4, 3)
b = np.random.randn(3, 2) # b.shape = (3, 2)
c = a * b

计算不成立因为这两个矩阵维度不匹配

Q2: 考虑以下代码段：

a = np.random.randn(3, 3)
b = np.random.randn(3, 1)
c = a * b

这会触发广播机制，b会被复制3次变成(3 * 3)，而 * 操作是元素乘法，所以c.shape = (3, 3)

本周编程作业

搭建一个能够 【识别猫猫】的简单的神经网络
本次作业参考【Kulbear】的github中的文章Logistic Regression with a Neural Network mindset

数据集地址

建立神经网络的主要步骤及关键代码：

1. 定义模型结构（例如输入特征的数量）

2. 初始化模型的参数

构建sigmoid()，初始化参数w和b

#标准化数据集
train_set_x = train_set_x_flatten / 255
test_set_x = test_set_x_flatten / 255

def sigmoid(z):
    s = 1 / (1 + np.exp(-z))
    return s

def initialize_with_zeros(dim):
    w = np.zeros(shape = (dim,1))
    b = 0
    #使用断言来确保我要的数据是正确的
    assert(w.shape == (dim, 1)) #w的维度是(dim,1)
    assert(isinstance(b, float) or isinstance(b, int)) #b的类型是float或者是int

    return (w , b)

3. 循环：
   3.1 计算当前损失（正向传播）
   3.2 计算当前梯度（反向传播）
   3.3 更新参数（梯度下降）

def propagate(w, b, X, Y):

    m = X.shape[1]

    #正向传播
    A = sigmoid(np.dot(w.T,X) + b) #计算激活值，请参考公式2。
    cost = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A))) #计算成本，请参考公式3和4。
    
    #反向传播
    dw = (1 / m) * np.dot(X, (A - Y).T) #请参考视频中的偏导公式。
    db = (1 / m) * np.sum(A - Y) #请参考视频中的偏导公式。

    #使用断言确保我的数据是正确的
    assert(dw.shape == w.shape)
    assert(db.dtype == float)
    cost = np.squeeze(cost)
    assert(cost.shape == ())
    
    #创建一个字典，把dw和db保存起来。
    grads = {
                "dw": dw,
                "db": db
             }
    return (grads , cost)

使用梯度下降更新参数，最小化成本函数$J$来学习 $w$ 和$b$
参数 $\theta =\theta -\alpha d\theta$

def optimize(w , b , X , Y , num_iterations , learning_rate , print_cost = True):
    
    costs = []
    
    for i in range(num_iterations):
        
        grads, cost = propagate(w, b, X, Y)
        
        dw = grads["dw"]
        db = grads["db"]
        
        w = w - learning_rate * dw
        b = b - learning_rate * db
        
        #记录成本
        if i % 100 == 0:
            costs.append(cost)
        #打印成本数据
        if (print_cost) and (i % 100 == 0):
            print("迭代的次数: %i ， 误差值： %f" % (i,cost))
        
    params  = {
                "w" : w,
                "b" : b }
    grads = {
            "dw": dw,
            "db": db } 
    return (params , grads , costs)

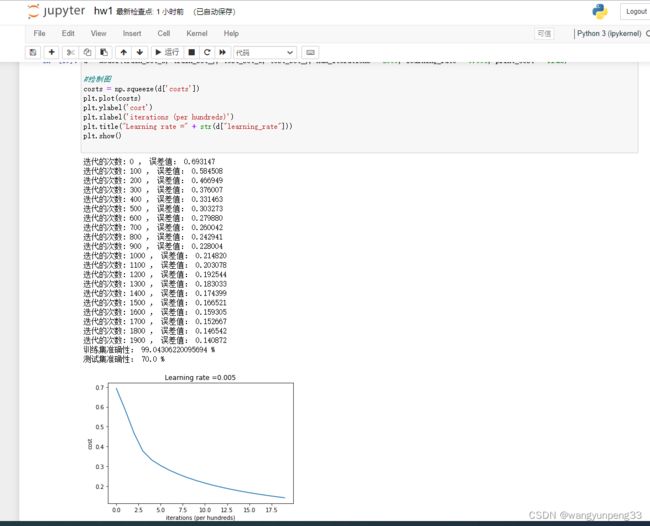
模型建好之后的实际测试结果：

机器学习算法

 机器学习算法可以分为三大类：

• 监督学习算法 (Supervised Algorithms） 在监督学习训练过程中，可以由训练数据集学到或建立一个模式（函数 / learning model），并依此模式推测新的实例。主要包括神经网络、支持向量机、K-近邻居法、朴素贝叶斯法、决策树等。
• 无监督学习算法 (Unsupervised Algorithms) 没有明确目的的训练方式，你无法提前知道结果是什么。常见的2类算法是：聚类、降维。
• 强化学习算法 (Reinforcement Algorithms) 主要基于决策进行训练，算法根据输出结果（决策）的成功或错误来训练自己，通过大量经验训练优化后的算法将能够给出较好的预测

基本的机器学习算法：

• 线性回归算法 Linear Regression
• 支持向量机算法 (Support Vector Machine,SVM)
• 最近邻居/k-近邻算法 (K-Nearest Neighbors,KNN)
• 逻辑回归算法 Logistic Regression
• 树算法 Decision Treek
• 平均算法 K-Means
• 随机森林算法 Random Forest
• 朴素贝叶斯算法 Naive Bayes
• 降维算法 Dimensional Reduction
• 梯度增强算法 Gradient Boosting

KNN(K Nearest Neighbor) K近邻（有监督算法，分类算法）

分类数据最简单有效的算法，优点是可以用来填充缺失值，可以处理非线性问题。调优方法在于K值的选择，k值太小，容易过拟合。缺点是对数据的局部结构非常敏感。计算量大，需要对数据进行规范化处理，使每个数据点都在相同的范围，因为需要求所有邻居的距离，所以效率低下，数据集较大时非常耗时。主要应用于样本数少，特征个数较少的数据集，KNN更适合处理一些分类规则相对复杂的问题，在推荐系统大量使用。

Decision Tree决策树（有监督算法，概率算法）
只接受离散特征，属于分类决策树。条件熵的计算 H(Label |某个特征) 这个条件熵反映了在知道该特征时，标签的混乱程度，可以帮助我们选择特征，选择下一步的决策树的节点。 决策树作为一种贪心算法，无法从全局的观点来观察决策树，从而难以调优。优点在于可解释性强，可视化。缺点是容易过拟合（通过剪枝避免过拟合），很难调优，准确率不高。决策树算法可以看成是把多个逻辑回归算法集成起来。

Naive Bayes朴素贝叶斯算法
基于概率论的贝叶斯定理，适用于特征之间的相互独立的场景，例如利用花瓣的长度和宽度来预测花的类型。“朴素”的内涵可以理解为特征和特征之间独立性强，从而降低了对数据量的要求。提供了利用已知值估计未知概率的方法。

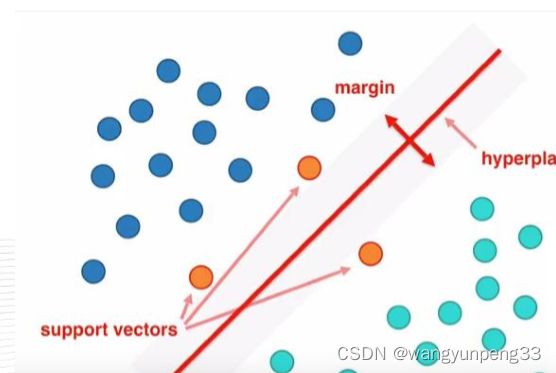
SVM（Support Vector Machine）支持向量机

寻找一个超平面$w^{T}x+b$将样本分为两类，且间隔最大。不易过拟合，适合处理复杂非线性问题。SVM算法是介于简单算法和神经网络之间的最好的算法。 只通过几个支持向量就确定了超平面，说明它不在乎细枝末节，所以不容易过拟合，处理复杂的非线性问题。缺点在于计算量大。



Dimensional Reduction 降维算法

降维有以下一系列原因：使数据更易使用，降低算法开销，去除噪声，使结果易懂。其中主成分分析适用于数值型数据，由于Numpy中的模块linalg可以用eig()求解出特征值和特征向量，方便我们实现PCA。
PCA大致步骤为去平均值，计算协方差矩阵，用linalg.eig()求解特征值特征向量，特征值排序，利用最大的N个特征向量构成的矩阵做空间变换。