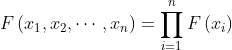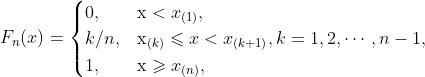数理统计（python）

一般认为，统计学是收集、分析、表述和解释数据的科学，统计学是一门处理数据的方法和技术的学科。

1.总体和样本 

研究对象的全体称为总体， 构成总体的每个成员称为个体 ,

总体就是一个概率分布，总体的数量指标就是服从该概率分布的一个随机变量。

一般来说，总体分为：有限总体和无限总体, 大多数我们说的总体是无限总体。 

为了了解总体的分布， 我们从总体中随机地抽取 n个个体， 记其指标值为 x1,x2,⋯, xn, 则 x1,x2,⋯,xn称为总体的一个样本,n 称为样本容量,或简称样本量，样本中的个体称为样品。 

样本的二重性 

一方面, 由于样本是从总体中随机抽取的， 抽取前无法预知它们的数值， 因此， 样本是一个随机变量， 用大写字母 X1,X2,⋯,Xn表示 

另一方面， 样本在抽取以后经观测就有确定的观测值， 因此， 样本又是一组数值， 此时用小写字母 x1,x2,⋯,xn表示是合适的。 

为了描述的简单，我们只用小写字母表示样本x1,x2,⋯,xn，不管样本是随机变量还是具体的数值，都用小写字母表示。 

简单随机抽样的需求

 从总体中抽取的样本具有代表性：具有代表性要求总体中每一个个体都有同等机会被选入样本中，也就意味着样本中的每一个样品xi与总体X有相同的分布，简称“同分布”。

从总体中抽取的样本具有独立性：具有独立性即要求样本中每一样品的取值不影响其他样品的取值， 也就意味着 x1,x2,⋯,xn之间相互独立。

 总结起来：在简单随机抽样这种抽样方法下，样本中的每一个样品x1,x2,⋯,xn之间独立同分布，同分布于总体分布，简称：iid。用简单随机抽样方法得到的样本称为简单随机样本，也简称样本。

设总体 X 具有分布函数 F(x),x1,x2,⋯,xn 为取自该总体的容量为 n 的样本，则样本联合分布函数为 

 

2.经验分布函数与直方图 

（1）经验分布函数： 

经验分布函数就是使用样本信息构造的分布函数近似未知的总体分布函数 

设 x1,x2,⋯,xn是取自总体分布函数为 F(x) 的样本， 若将样本观测值由小到大进行排列， 记为 x(1),x(2),⋯,x(n), 则 x(1),x(2),⋯,x(n) 称为有序样本， 用有序样本定义如下函数 

 

则 Fn(x)是一非减右连续函数， 且满足 

 

由此可见， Fn(x)是一个分布函数， 称 Fn(x)为该样本的经验分布函数。 

（2）直方图：频数直方图和频率直方图 

直方图是数值数据分布的精确图形表示， 这是一个连续变量（定量变量）的概率分布的估计

# 频数直方图
x_samples = np.random.randn(1000)
plt.hist(x_samples, bins=10,color='blue',alpha=0.6)  # bins=10代表10根柱子
plt.xlabel("x")
plt.ylabel("频数 n")
plt.title("频数直方图")
plt.show()

# 频率直方图
x_samples = np.random.randn(1000)
plt.hist(x_samples, bins=10,color='blue',alpha=0.6,density=True)  # bins=10代表10根柱子
plt.xlabel("x")
plt.ylabel("频率 p")
plt.title("频率直方图")
plt.show()

 3.统计量与三大抽样分布

 设 x1,x2,⋯,xn 为取自某总体的样本， 若样本函数 T=T(x1,x2,⋯,xn) 中不含有任何末知参数， 则称 T 为统计量。统计量的分布称为抽样分布。

值得注意的是：统计量由样本决定，从而统计量因样本而异，对于同一总体，由于抽取样本是具有随机性的，因此抽取不同的样本，统计量就不同，从而统计量也是一个随机变量。统计量的分布称为抽样分布。虽然统计量不依赖于任何参数，但统计量的分布一般依赖于未知参数。