PMSM FOC位置环S曲线控制算法(恒定急动度)
文章目录
-
- 一 原理
- 二 代码
之前做FOC位置环控制的时候,简单地加了一个S曲线控制,参考链接如下: FOC 单电阻采样 位置环控制伺服电机
这里面代码实现其实就是在每step个ADC中断中,根据函数 f ( x ) = 1 1 + e − x \Large f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1生成一个uint16的S曲线定点数组,每次计算位置增加的比例,进而设置位置环的目标值。当然还需要考虑一些问题,比如S曲线有一些地方很平缓,增量不高,所以在还没到step个ADC中断的时候,PID就已经收敛了,所以电机就会在目标位置轻微抖动。当然这个BUG稍稍修改一下代码就可以避免了,但是有没有更好的控制方法呢?
一 原理
如图所示,如果采用恒定加速度,先以加速度a加速,再匀速,再以加速度-a减速。
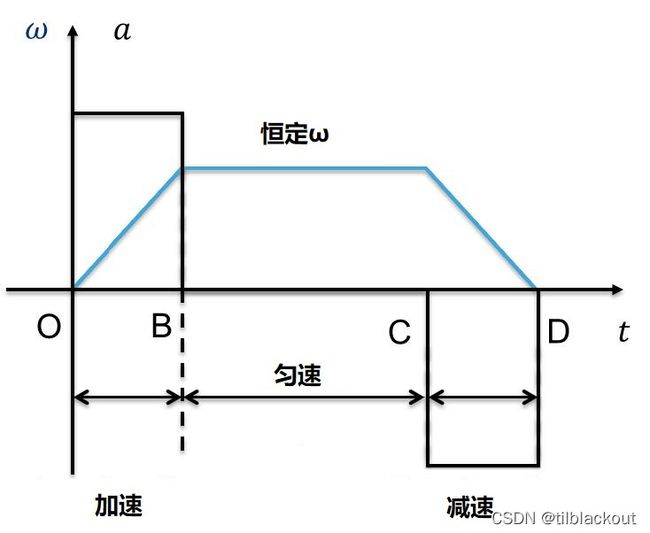
但是这样的话,加速度就有一个阶跃变化,这在物理上是不可实现的,同时也会损坏电机。所以这里考虑将对加速度进行微分,就可以得到急动度(Jerk/Jolt),它用物理量J表示,即 J = d a d t \Large J=\frac{da}{dt} J=dtda。
这样就可以让加速度以梯形波形式变化:

那么到底这样的加速度函数会产生什么样的速度和角度曲线呢?
编写Matlab程序,对加速度求积分得到速度曲线,对速度曲线求积分得到角度曲线。这里初始化J=1、A=1(单位控制时间),曲线形状不受这两个变量大小的影响,仅仅会影响曲线的宽窄程度。
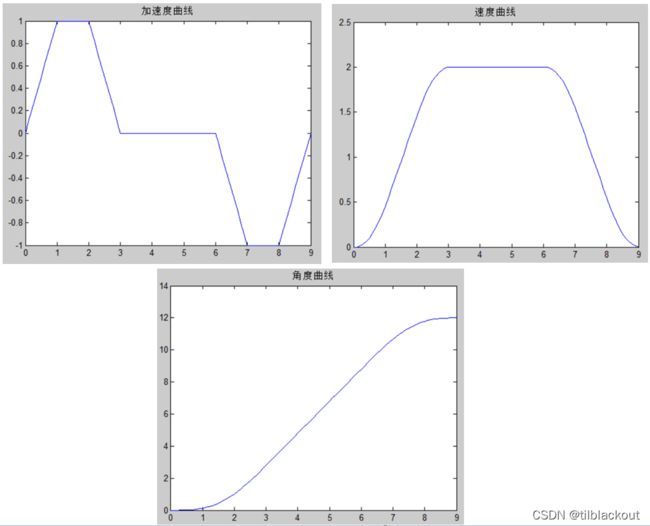
可以看到角度的变化正好是S曲线,有了这样的结果,我们开始对整个过程进行数学分析。这里以加速阶段为例进行分析,如下图所示,将加速阶段分为三段,持续时间t=A。

(1)Ⓞ->①阶段:恒定+J
初始时刻 a 0 = 0 a_{0} = 0 a0=0、 ω 0 = 0 \omega _{0} = 0 ω0=0、 θ 0 = 0 \theta _{0} = 0 θ0=0。
{ a 1 = a 0 + J t = J A ω 1 = ω 0 + ∫ 0 t a 1 d t = ω 0 + a 0 t + 1 2 J t 2 = 1 2 J A 2 θ 1 = θ 0 + ∫ 0 t ω 1 d t = θ 0 + ω 0 t + 1 2 a 0 t 2 + 1 6 J t 3 = 1 6 J A 3 \left\{\begin{matrix} a_{1} = a_{0} + Jt = JA \\ \omega_{1} = \omega_{0} + \int_{0}^{t}a_{1}dt =\omega_{0} + a_{0}t + \frac{1}{2}Jt^{2} = \frac{1}{2}JA^{2} \\ \theta_{1} = \theta_{0} + \int_{0}^{t}\omega_{1}dt = \theta_{0} + \omega_{0}t + \frac{1}{2}a_{0}t^{2}+\frac{1}{6}Jt^{3} = \frac{1}{6}JA^{3} \end{matrix}\right. ⎩⎨⎧a1=a0+Jt=JAω1=ω0+∫0ta1dt=ω0+a0t+21Jt2=21JA2θ1=θ0+∫0tω1dt=θ0+ω0t+21a0t2+61Jt3=61JA3
(2)①->②阶段:J=0,a恒定
{ a 2 = a 1 = J A ω 2 = ω 1 + ∫ 0 t a 2 d t = ω 1 + a 2 t = 3 2 J A 2 θ 2 = θ 1 + ∫ 0 t ω 2 d t = θ 1 + ω 1 t + 1 2 a 2 t 2 = 7 6 J A 2 \left\{\begin{matrix} a_{2} = a_{1} = JA \\ \omega_{2} = \omega_{1} + \int_{0}^{t}a_{2}dt= \omega_{1}+a_{2}t = \frac{3}{2}JA^{2} \\ \theta_{2} = \theta_{1} + \int_{0}^{t}\omega_{2}dt = \theta_{1}+\omega_{1}t+\frac{1}{2}a_{2}t^{2}= \frac{7}{6}JA^{2} \end{matrix}\right. ⎩⎨⎧a2=a1=JAω2=ω1+∫0ta2dt=ω1+a2t=23JA2θ2=θ1+∫0tω2dt=θ1+ω1t+21a2t2=67JA2
(3)②->③阶段:恒定-J
{ a 3 = a 2 − J t = 0 ω 3 = ω 2 + ∫ 0 t a 3 d t = ω 2 + a 2 t − 1 2 J t 2 = 2 J A 2 θ 3 = θ 2 + ∫ 0 t ω 3 d t = θ 2 + ω 2 t + 1 2 a 2 t 2 − 1 6 J A 2 = 3 J A 3 \left\{\begin{matrix} a_{3} = a_{2} - Jt=0 \\ \omega_{3} = \omega_{2} + \int_{0}^{t} a_{3}dt= \omega_{2} + a_{2}t-\frac{1}{2}Jt^{2}=2JA^{2} \\ \theta_{3} = \theta_{2}+\int_{0}^{t} \omega_{3}dt=\theta_{2} + \omega_{2}t + \frac{1}{2}a_{2}t^{2}-\frac{1}{6}JA^{2}=3JA^{3} \end{matrix}\right. ⎩⎨⎧a3=a2−Jt=0ω3=ω2+∫0ta3dt=ω2+a2t−21Jt2=2JA2θ3=θ2+∫0tω3dt=θ2+ω2t+21a2t2−61JA2=3JA3
这样就计算出了加速阶段转过的角度,而减速过程与加速过程对称,故 θ a c c e l e r a t e = θ d e c e l e r a t e = θ 3 = 3 J A 3 \theta_{accelerate} = \theta_{decelerate}= \theta_{3} = 3JA^{3} θaccelerate=θdecelerate=θ3=3JA3。中间是加速度为0,速度为 ω 3 \omega _{3} ω3,时间为3A的匀速阶段。
最终得到总旋转角度 θ t o t a l = θ a c c e l e r a t e + ω 3 t + θ d e c e l e r a t e = 12 J A 3 \theta_{total} = \theta_{accelerate} + \omega_{3}t+\theta_{decelerate} = 12JA^{3} θtotal=θaccelerate+ω3t+θdecelerate=12JA3
二 代码
参考代码:X-CUBE-MCSDK库
1、位置环结构体
了解了前面的原理后,这些变量的含义就很清楚了。原本角度相关的变量是float类型的,这里为了方便和系统中的电角度变量统一,所以这里都改为了int16类型。而急动度、加速度、时间等参数不得不设置为浮点型,因为特定旋转角度和时间对应的急动度不一定是整数。
typedef enum {
TC_READY_FOR_COMMAND = 0,
TC_MOVEMENT_ON_GOING = 1, /* MOVE模式 */
TC_TARGET_POSITION_REACHED = 2, /* 到达位置 */
} PosCtrlStatus_t;
typedef struct
{
float SamplingTime;
float MovementDuration;
float SubStep[6];
float SubStepDuration;
float ElapseTime;
float Jerk;
float CruiseSpeed;
float Acceleration;
float Omega;
float OmegaPrev;
float ThetaPrev;
int16_t StartingAngle;
int16_t FinalAngle;
int16_t AngleStep;
int16_t Theta;
int16_t hMaxTorque;
int16_t flag;
PosCtrlStatus_t PositionCtrlStatus;
PID_Handle_t *PIPos;
} PosControl_Handle_t;
2、参数计算与状态切换
计算旋转参数,如急动度、巡航速度(CruiseSpeed),然后初始化时间、加速度、角速度、角度为初始值,最后将状态设置为TC_MOVEMENT_ON_GOING,这表示在中频任务调用位置环函数中将执行我们的S曲线位置环过程。
void TC_MoveCommand(PosControl_Handle_t *pHandle, int16_t startingAngle, int16_t angleStep, float movementDuration)
{
float fMinimumStepDuration;
if ( (pHandle->PositionCtrlStatus == TC_READY_FOR_COMMAND) && (movementDuration > 0) )
{
/* 总时间 */
fMinimumStepDuration = (9.0f * pHandle->SamplingTime);
/* 传入的运动时间参数是浮点数,但它只能是最小时间的整数倍 */
pHandle->MovementDuration = (float)((int)(movementDuration / fMinimumStepDuration)) * fMinimumStepDuration;
pHandle->StartingAngle = startingAngle;
pHandle->AngleStep = angleStep;
pHandle->FinalAngle = startingAngle + angleStep;
/* 将总持续时间分为9段 */
pHandle->SubStepDuration = pHandle->MovementDuration / 9.0f;
// 加速阶段
pHandle->SubStep[0] = 1 * pHandle->SubStepDuration; /* Sub-step 1 of acceleration phase */
pHandle->SubStep[1] = 2 * pHandle->SubStepDuration; /* Sub-step 2 of acceleration phase */
pHandle->SubStep[2] = 3 * pHandle->SubStepDuration; /* Sub-step 3 of acceleration phase */
// 减速阶段
pHandle->SubStep[3] = 6 * pHandle->SubStepDuration; /* Sub-step 1 of deceleration phase */
pHandle->SubStep[4] = 7 * pHandle->SubStepDuration; /* Sub-step 2 of deceleration phase */
pHandle->SubStep[5] = 8 * pHandle->SubStepDuration; /* Sub-step 3 of deceleration phase */
// J = DeltaTheta/(12 * A * A * A)
pHandle->Jerk = pHandle->AngleStep / (12 * pHandle->SubStepDuration * pHandle->SubStepDuration * pHandle->SubStepDuration);
// Speed cruiser = 2*J*A*A)
pHandle->CruiseSpeed = 2 * pHandle->Jerk * pHandle->SubStepDuration * pHandle->SubStepDuration;
pHandle->ElapseTime = 0.0f;
pHandle->Omega = 0.0f;
pHandle->Acceleration = 0.0f;
pHandle->Theta = startingAngle;
pHandle->PositionCtrlStatus = TC_MOVEMENT_ON_GOING;
}
}
3、位置环函数
这里就是根据之前计算的急动度等参数,执行位置环过程,最终计算出theta用于位置环PID控制的目标值中。但由于浮点运算的误差,最终值会和目标值有一定误差,有可能超过目标值,也可能小于目标值。所以在到达ElapseTime,直接将theta设置为最终的角度值。这里加了个判断,防止位置过调。
int16_t delta_end,delta_tmp;
int16_t get_delta()
{
int16_t tmp;
tmp = PosCtrlM.Theta - PosCtrlM.FinalAngle;
return tmp;
}
uint8_t flag_end=0;
void TC_MoveExecution(PosControl_Handle_t *pHandle)
{
float jerkApplied = 0;
if(pHandle->PositionCtrlStatus != TC_MOVEMENT_ON_GOING)
{
return;
}
if (pHandle->ElapseTime < pHandle->SubStep[0]) // 1st Sub-Step interval time of acceleration phase
{
jerkApplied = pHandle->Jerk;
}
else if (pHandle->ElapseTime < pHandle->SubStep[1]) // 2nd Sub-Step interval time of acceleration phase
{
}
else if (pHandle->ElapseTime < pHandle->SubStep[2]) // 3rd Sub-Step interval time of acceleration phase
{
jerkApplied = -(pHandle->Jerk);
}
else if (pHandle->ElapseTime < pHandle->SubStep[3]) // Speed Cruise phase (after acceleration and before deceleration phases)
{
pHandle->Acceleration = 0.0f;
pHandle->Omega = pHandle->CruiseSpeed;
}
else if (pHandle->ElapseTime < pHandle->SubStep[4]) // 1st Sub-Step interval time of deceleration phase
{
jerkApplied = -(pHandle->Jerk);
}
else if (pHandle->ElapseTime < pHandle->SubStep[5]) // 2nd Sub-Step interval time of deceleration phase
{
}
else if (pHandle->ElapseTime < pHandle->MovementDuration) // 3rd Sub-Step interval time of deceleration phase
{
jerkApplied = pHandle->Jerk;
}
else
{
jerkApplied = pHandle->Jerk;
}
delta_end = get_delta();
//a = a0 + jt
pHandle->Acceleration += jerkApplied * pHandle->SamplingTime;
//v = v0 + at
pHandle->Omega += pHandle->Acceleration * pHandle->SamplingTime;
//θ = θ0 + vt
pHandle->Theta += pHandle->Omega * pHandle->SamplingTime;
/* 变化小时,0~16384测试,最后会卡一下再继续旋转,因为前面减速认为已经到目标位置了omega几乎为0,随着时间推移才变大 */
delta_tmp = get_delta();
if((delta_end < 0 && delta_tmp > 0) || (delta_end > 0 && delta_tmp < 0) || (delta_end == 0))
{
pHandle->Theta = pHandle->FinalAngle;
pHandle->PositionCtrlStatus = TC_READY_FOR_COMMAND;//REACH后不变为TC_READY_FOR_COMMAND
flag_end = 0;
return;
}
pHandle->ElapseTime += pHandle->SamplingTime;
4、位置环函数
该函数在中频任务中执行。
void TC_PositionRegulation(PosControl_Handle_t *pHandle)
{
int16_t wMecAngleRef;
int16_t wMecAngle;
int16_t wError;
int32_t hTorqueReference;
TC_MoveExecution(pHandle);
wMecAngleRef = pHandle->Theta;
wMecAngle = ENCODER_M._Super.hMecPosition;
wError = wMecAngle - wMecAngleRef;
hTorqueReference = PID_Controller(pHandle->PIPos, wError);
if(hTorqueReference < 0)
{
if(hTorqueReference < -pHandle->hMaxTorque)
hTorqueReference = -pHandle->hMaxTorque;
}
else
{
if(hTorqueReference > pHandle->hMaxTorque)
hTorqueReference = pHandle->hMaxTorque;
};
FOCVars.hTeref = hTorqueReference;
}
5、更改位置API
在我的应用中,位置环仅在一圈内进行旋转,所以前面设置的是int16类型的角度。在有些应用中,需要旋转多圈。如输入70000,就是先旋转2圈(65535),在旋转4465,这就需要将前面的变量设置为uint32类型。这里的代码也需要做小小的修改。
void MCI_ExecPositionCommand( PosControl_Handle_t * pHandle, int16_t FinalPosition, float Duration )
{
int16_t currentPosition = ENCODER_M._Super.hMecPosition;
int16_t angleStep = FinalPosition - currentPosition;
pHandle->PositionCtrlStatus = TC_READY_FOR_COMMAND;
TC_MoveCommand(pHandle, currentPosition, angleStep, Duration);
}
6、待解决
浮点运算的误差产生了很多问题:
- 将float的角度转为int16,每次计算的角度本来是浮点数被化成了整数,所以可以多用一个浮点变量来记录小数点后的角度,最后忽略掉小数点赋值给int16的电角度,这样不会有累积的更多误差。
- 旋转一圈误差可能还可以接收,但如果旋转多圈,浮点运算次数变多,最终结束后与目标值的偏差就很大,然后运动过程结束,直接设置为目标值,电机就会有一个迅速旋转到目标值的过程,误差越大越明显。实际测试,不仅最后的值会小于目标值,还有可能大于目标值,也就是会超调。
我的解决办法是:由于我们对旋转时间的要求可能没有那么高,所以就根据用户设置的值,寻找一个近似的时间,这样计算出来的急动度为整数,或者说小数部分正好是 2 − i 2^{-i} 2−i,这样后续的计算就没有浮点误差。如果大家还有什么好的解决办法,欢迎讨论。