【CV-baseline】05GoogLeNet_v3(笔记)
论文标题:Rethinking the Inception Architecture for Computer Vision
作者: Christian Szegedy etc.
单位: Google Inc.
时间: 2015
学习目标
- 模型设计准则
- 模型设计技巧
- 卷积分解
- 辅助分类层探讨
- 特征图下降策略
- 标签平滑
- 低分辨率图像分类
- 测试技巧
- Multi-crop测试
- 多模型融合
论文导读
研究背景
GoogLeNet–V1 采用多尺度卷积核, 1 × 1 1\times 1 1×1卷积操作, 辅助损失函数,实现更深的22层卷积神经网络,夺得 ILSVRC-2014 分类和检测冠军,定位亚军GoogLeNet-V2 基础上加入BN层,并将 5 × 5 5\times5 5×5卷积全面替 换为2个3*3卷积堆叠的形式,进一步提高模型性能。
但是VGG网络模型大,参数多,计算量大,不适用于真实场景
研究成果
- 提出inception-v2和inception-v3,inception-v3模型获得了ILSVRC分类任务SOTA
- 提出4个网络模型设计准则,为模型设计提供参考
- 提出卷积分解、高效率降低特征图分辨率方法和标签平滑技巧。提升了网络速度和精度
研究意义
- 总结模型设计准则,为卷积神经网络模型设计提供参考
- 提出3个技巧,结合Inception,奠定Inception系列最常用模型——Inception-V3
注意:GoogLeNet-V2(论文) 不是 Inception-V2, Inception-V2是GoogLeNet-V3(论文) 中提出的
论文泛读
摘要
- 介绍背景:自2014年以来,深度卷积神经网络成为主流,在多个任务中获得优异成绩
- 提出问题:目前精度高的卷积神经网络,参数多,计算量大,存在落地困难问题
- 解决问题:本文提出分解卷积及正则化策略,提升深度卷积神经网络速度和精度
- 本文成果:单模型+single crop,top-5, 5.6%; 模型融合+multi-crop,top-5,3.5%
论文精读
网络设计准则
通过大量实验得出的结论,并无理论证明
- 尽量避免信息瓶颈,通常发生在池化层,即特征图变小,信息量减少,类似一个瓶颈
- 采用更高维的表示方法能够更容易的处理网络的局部信息
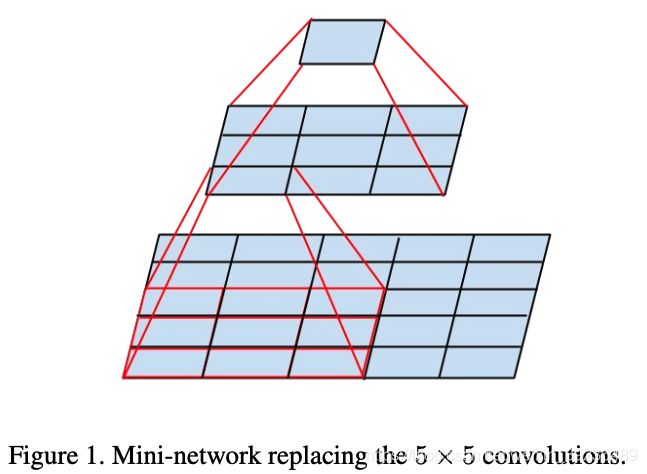
- 大的卷积核可以分解为数个小卷积核,且不会降低网络能力
- 把握好深度和宽度的平衡
【第2、4点根本就是废话】
卷积分解(factorizing convolutions)
卷积分解1
大卷积核分解为小卷积核堆叠。 1个 5 × 5 5\times 5 5×5卷积分解为2个 3 × 3 3\times 3 3×3卷积。参数减少了1-(9+9)/25 = 28%
卷积分解2
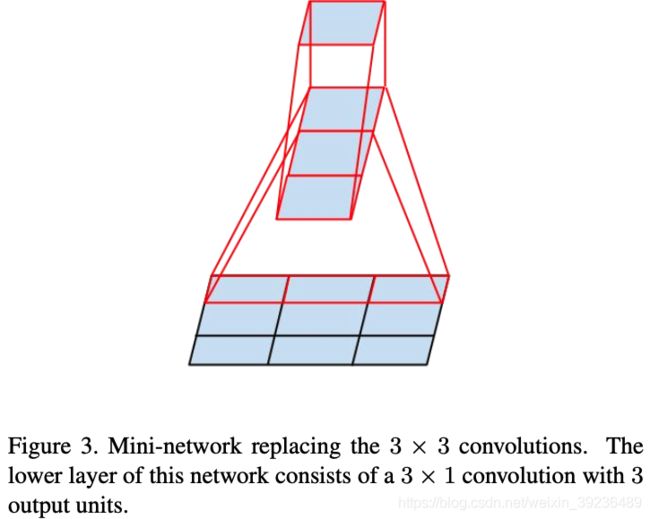
1个 n × n n\times n n×n卷积分解为 1 × n 1\times n 1×n卷积和 n × 1 n\times 1 n×1卷积堆叠。对于 3 × 3 3\times 3 3×3而言,参数减少了1-(3+3)/9=33%
注意:非对称卷积在后半段网络使用效果才好,特别是特征图分辨率在12-20之间,本文在分辨率为 17 × 17 17\times 17 17×17的时候使用非对称卷积分解
辅助分类层
GoogLeNet-V1中提出辅助分类层,用于缓解梯度消失, 提升低层的特征提取能力 本文对辅助分类层进行分析,得出结论:
- 辅助分类层在初期起不到作用,在后期才能提升网
络性能 - 移除第一个辅助分类层不影响精度
- 辅助分类层可辅助低层提取特征是不正确的
- 辅助分类层对模型起到正则的作用
- googlenet-v3在 17 × 17 17\times 17 17×17特征图结束接入辅助分类层
高效特征图下降策略
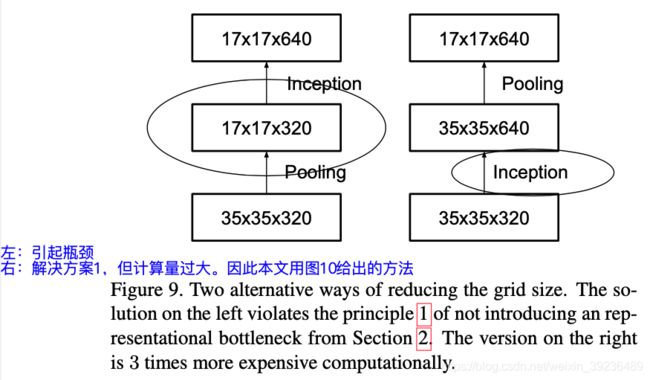
传统池化方法存在信息表征瓶颈问题,违反了设计准则1,也就是特征图信息变少了(如图9左所示)
简单解决方法:先用卷积将特征图通道数翻倍,再用池化。存在问题:计算量过大
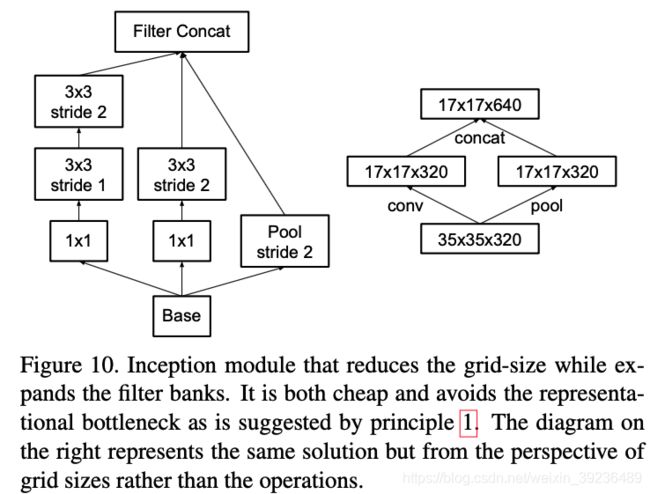
进一步策略:用卷积得到一半特征图,用池化的到一半特征图。用较少的计算量获得较多的信息,避免信息表征瓶颈。
base是 35 × 35 × 320 35\times 35\times 320 35×35×320, concat之后就变成了 17 × 17 × 640 17\times 17\times 640 17×17×640.
该inception-module用于 35 × 35 35\times 35 35×35下降至 17 × 17 17\times 17 17×17以及 17 × 17 17\times 17 17×17下降至 8 × 8 8\times 8 8×8
标签平滑
传统的one-hot编码存在问题:过度自信,导致过拟合
文中提出标签平滑:把one-hot中概率为1的那一项进行衰减,避免过度自信,衰减的那部分confidence平均分到每一个类别中。
举例:4分类任务,label=(0, 1, 0, 0)
label smoothing: ( 0.001 4 , 1 − 0.001 + 0.001 4 , 0.001 4 , 0.001 4 ) = ( 0.00025 , 0.99925 , 0.00025 , 0.00025 ) (\dfrac{0.001}{4}, 1-0.001+\dfrac{0.001}{4}, \dfrac{0.001}{4}, \dfrac{0.001}{4})=(0.00025, 0.99925, 0.00025, 0.00025) (40.001,1−0.001+40.001,40.001,40.001)=(0.00025,0.99925,0.00025,0.00025)
标签平滑公式
回顾交叉熵定义: H ( q , p ) = − ∑ k = 1 K log ( p k ) q k \mathrm{H}(q, p)=-\sum_{k=1}^{K} \log \left(p_{k}\right) q_{k} H(q,p)=−∑k=1Klog(pk)qk。这里k是指有多少种标签类别
对于这里的问题, q是one-hot标签分布 。还是用上面的例子作为一个样本来分析。 q = [ 0 , 1 , 0 , 0 ] q=\left[0, 1, 0, 0\right] q=[0,1,0,0], 假如 p = q p=q p=q,那么 H ( q , p ) = − ( 0 log 0 + 1 log 1 + 0 log 0 + 0 log 0 ) = 0 H(q, p)=-(0\log0+1\log1 +0\log0+0\log0)=0 H(q,p)=−(0log0+1log1+0log0+0log0)=0.
现在我们考虑标签平滑,把 q q q平滑变为 q ′ q^{\prime} q′,让模型输出的 p p p分布去逼近 q ′ q^{\prime} q′。假设添加的扰动是 ϵ = 0.001 \epsilon=0.001 ϵ=0.001,我们有
q ′ ( k ∣ x ) = ( 1 − ε ) δ k , y + ϵ u ( k ) = ( 1 − ε ) δ k , y + ϵ K q^{\prime}(k \mid x)=(1-\varepsilon) \delta_{k, y} + \epsilon u(k)\\ =(1-\varepsilon) \delta_{k, y} + \frac{\epsilon}{K} q′(k∣x)=(1−ε)δk,y+ϵu(k)=(1−ε)δk,y+Kϵ
这里y表示标签1出现的位置索引,这里y=1。也就是说,对于k=y=1, δ = 1 \delta=1 δ=1, 对于其他的位置 k = 0 , 2 , 3 k=0, 2, 3 k=0,2,3, δ = 0 \delta=0 δ=0。因此
q ′ ( 0 ∣ x ) = ϵ u ( 0 ) = 0.001 / 4 = 0.00025 q ′ ( 1 ∣ x ) = ( 1 − ϵ ) + ϵ u ( 1 ) = 0.999 + 0.001 / 4 = 0.99925 q^{\prime}(0 \mid x) = \epsilon u(0) = 0.001 / 4=0.00025\\ q^{\prime}(1 \mid x) =(1-\epsilon) + \epsilon u(1) = 0.999 + 0.001 / 4=0.99925 q′(0∣x)=ϵu(0)=0.001/4=0.00025q′(1∣x)=(1−ϵ)+ϵu(1)=0.999+0.001/4=0.99925
标签平滑后的交叉熵损失函数是
l H ( q ′ , p ) = − ∑ k = 1 K log ( p k ) q k = − ∑ k = 1 K log ( p k ) [ ( 1 − ε ) δ k , y + ε K ] = − ∑ k = 1 K log ( p k ) ( 1 − ε ) δ k , y + [ − ∑ k = 1 K log ( p k ) ε k ] = ( 1 − ε ) [ − ∑ k = 1 K log ( p k ) δ k , y ] + ε [ − ∑ k = 1 K log ( p k ) 1 k ] = ( 1 − ε ) H ( q , p ) + ϵ H ( u , p ) \begin{aligned}{l} H(q^{\prime},p) &= -\sum_{k=1}^{K} \log \left(p_{k}\right) q_{k}\\ &= -\sum_{k=1}^{K} \log \left(p_{k}\right)\left[(1-\varepsilon) \delta_{k, y}+\frac{\varepsilon}{K}\right]\\ &= -\sum_{k=1}^{K} \log \left(p_{k}\right)(1-\varepsilon) \delta_{k, y}+\left[-\sum_{k=1}^{K} \log \left(p_{k}\right) \frac{\varepsilon}{k}\right]\\ &=(1-\varepsilon) \left[-\sum_{k=1}^{K} \log \left(p_{k}\right) \delta_{k, y}\right]+\varepsilon \left[-\sum_{k=1}^{K} \log \left(p_{k}\right) \frac{1}{k}\right]\\ &=(1-\varepsilon) H(q, p)+\epsilon H(u, p) \end{aligned} lH(q′,p)=−k=1∑Klog(pk)qk=−k=1∑Klog(pk)[(1−ε)δk,y+Kε]=−k=1∑Klog(pk)(1−ε)δk,y+[−k=1∑Klog(pk)kε]=(1−ε)[−k=1∑Klog(pk)δk,y]+ε[−k=1∑Klog(pk)k1]=(1−ε)H(q,p)+ϵH(u,p)
这里要注意, − ∑ k = 1 K log ( p k ) δ k , y = H ( q , p ) = − ∑ k = 1 K log ( p k ) q k -\sum_{k=1}^{K} \log \left(p_{k}\right) \delta_{k, y}= H(q, p)=-\sum_{k=1}^{K} \log \left(p_{k}\right) q_{k} −∑k=1Klog(pk)δk,y=H(q,p)=−∑k=1Klog(pk)qk.这是因为只有k=y=1的时候才有 q = 1 , δ k , y = 1 q=1, \delta_{k, y}=1 q=1,δk,y=1。 平滑后的交叉熵损失函数可以看出,现在我们有了两个交叉熵,分别是原来的交叉熵,还有扰动的平均分布与预测之间的交叉熵。最后的交叉熵结果就是这两个交叉熵的加权平均,其实就是通过引入平均分布使得标签不那么分布集中,达到正则的效果。
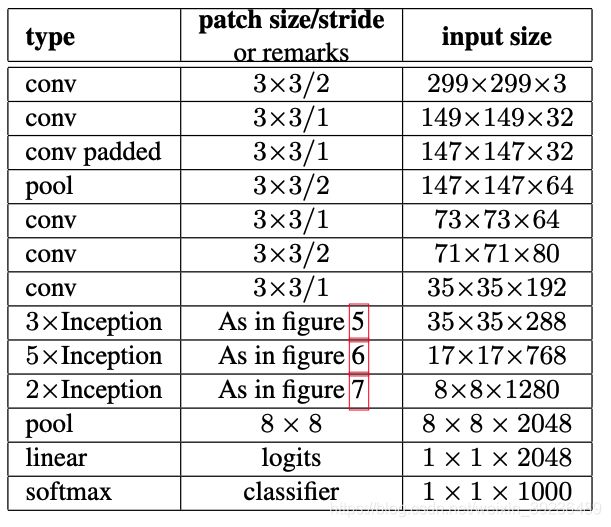
Inception-v2/3结构
Inception-V2
针对V1主要变化:
- 采用3个 3 × 3 3\times 3 3×3卷积替换1个 7 × 7 7\times 7 7×7卷积,并且在第一个卷积就采用stride=2来降低分辨率
- 第二个3个 3 × 3 3\times 3 3×3卷积,在第2个卷积才下降分辨率
- 第一个block增加一个inception-module,第一个 inception-module只是将 5 × 5 5\times 5 5×5卷积替换为2个 3 × 3 3\times 3 3×3卷积
- 第二个block,处理 17 × 17 17\times 17 17×17特征图,采用非对称卷积
- 第三个block,处理 8 × 8 8\times 8 8×8特征图,遵循准则2,提出拓展的卷积
- 最后输出2048个神经元,V1是1024个神经元
Inception-V2 和 V3
InceptionV3:在InceptionV2基础上改进4点
- 采用RMSProp优化方法
- 采用Label Smoothing正则化方法
- 采用非对称卷积提取 17 × 17 17\times 17 17×17特征图
- 采用带BN的辅助分类层
低分辨率图像分类策略
低分辨率图片分类在目标检测中广泛应用,而如何有效对低分辨率图像进行分类值得思考。如果直接把低分辨率图片resize成大尺寸图片,分辨率更低,作用不大。
本文方案:
-
对于 151 × 151 151\times 151 151×151图像,将第一个卷积层stride=2改为stride=1,
-
对于 79 × 79 79\times 79 79×79图像, stride=2改为stride=1,移除第一个池化层
借鉴思路:修改网络模型头部stride和池化,来处理低分辨率图片, 可尽可能的保留原网络模型结构,不损失网络精度。
实验结果分析
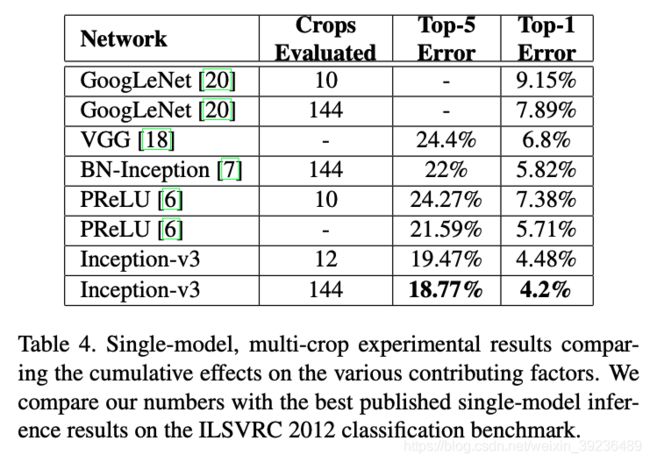
GoogLeNet系列对比
对比GoogLeNet-V1、V2,以及Inception-V2和本文采用的 4个技巧,得到最优的Inception-V2+BN+auxiliary+标签平滑+卷积分解 7 × 7 7\times 7 7×7 (也就是Inception-V3)
单模型对比
单模型上横向对比,Inception-V3优于目前各模型
多模型融合对比
采用4个Inception-v3进行融合,得到当时SOTA, Top5-error为 3.58%
论文总结
关键点&创新点
- 非对称卷积分解:减少参数计算量,为卷积结构设计提供新思路
- 高效特征图下降策略:利用stride=2的卷积与池化,避免信息表征瓶颈
- 标签平滑:避免网络过度自信,减轻过拟合
启发点
- CNN的分类是CNN视觉任务的基础:在分类上表现好的CNN,通常在其它视觉任务中表现也良好
- Google很多论文的最优结果均是通过大量实验得出,一般玩家难以复现
- 非对称卷积分解在分辨率为12-20的特征图上效果较好,且用 1 × 7 1\times 7 1×7和 7 × 1 7\times 1 7×1进行特征提取
- 在网络训练初期,辅助分类层的加入并没有加快网络收敛,在训练后期,才加快网络的收敛 (是否可针对性的设定训练方式?论文中并未详细说明这一点)
- 移除两个辅助分类层中的第一个,并不影响网络性能
- 标签平滑参数设置,让非标签的概率保持在 1 0 − 4 10^{-4} 10−4左右, 也就是根据任务的变化而变化,设置不同的超参数值 ϵ \epsilon ϵ. 【这里有点技巧,在本文中分类数量是1000,那么 u ( k ) = 1 / 1000 = 0.001 , ϵ = 0.1 , ϵ u = 0.001 × 0.1 = 1 0 − 4 u(k)=1/1000=0.001, \epsilon=0.1, \epsilon u=0.001\times 0.1=10^{-4} u(k)=1/1000=0.001,ϵ=0.1,ϵu=0.001×0.1=10−4, 如果任务换成其他,比如分类数量是10, 那么 u ( k ) = 0.1 u(k)=0.1 u(k)=0.1, ϵ \epsilon ϵ就可以变为 1 0 − 4 0.1 = 0.001 \dfrac{10^{-4}}{0.1}=0.001 0.110−4=0.001 】