CMSA-Net论文和代码笔记

最近比较关注self-attention在CV方面的应用。最近，看到一篇2019年的CVPR文章Cross-Modal Self-Attention Network for Referring Image Segmentation，同时涉及了CV和NLP领域，结果也比较有趣。
论文链接：https://arxiv.org/abs/1904.04745
代码链接：https://paperswithcode.com/paper/cross-modal-self-attention-network-for#code

论文笔记

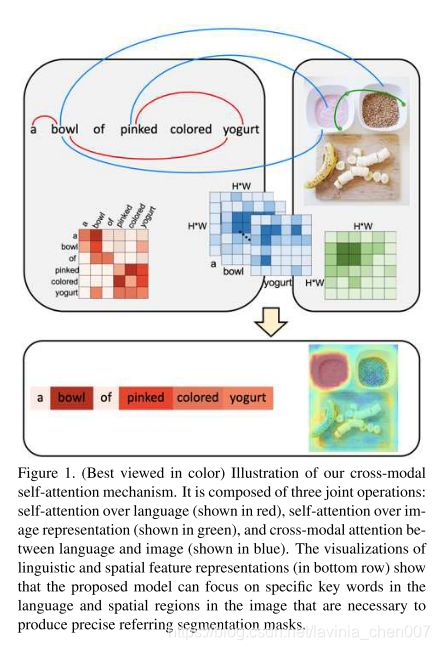
Given an input image and a natural language expression, the goal is to segment the object referred by the language expression in the image

这篇文章要完成的任务是，当给定一张图片和一句自然语言表达，网络能据此分割出表达中指代的物件。

之前工作的问题是

Existing works in this area treat the language expression and the input image separately in their representations. They do not sufficiently capture long-range correlations between these two modalities.

图片和语言表达的表示是分开进行的，也就意味着二者之间长距离的相关性无法被充分捕捉和利用。

本文提取了一个全新的模块cross-modal self-attention (CMSA) module， 能够有效的捕捉视觉和语言学特征长距离的依赖性；以及一个gated multi-level fusion module，能够有选择性地根据图像的不同层级整合自关注跨模态（self-attentive cross-modal）特征。

下图是CMSA模块工作机制的一个示例。

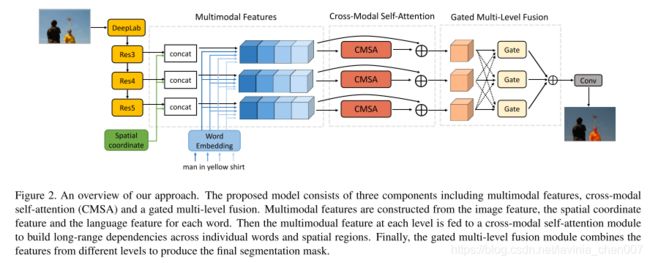
网络结构

网络结构如下图

多模态特征

图像特征：通过一个CNN（DeepLab）提取
指代表达：每个词表示为一个词嵌入向量
空间坐标特征(spatial coordinate feature)：8维，前3个维度对归一化的水平位置进行编码；接下来的3个维度对归一化的垂直位置进行编码；最后两个维度对归一化的图像宽和高进行编码。
多模态特征：每一个空间坐标对应的图像特征、词向量和空间坐标特征进行级联形成多模态特征。

对应位置$p$和第$n$个词的多模态特征$f_{pn}$为：
$f_{pn}=Concat(\frac{v_p}{\Vert v_p{\Vert }_2},\frac{e_n}{\Vert e_p{\Vert }_2},s_p)$
定义可具体参见文中3.1部分。
$F=\{f_{pn},\forall p,\forall n\}$不同空间位置和词语特征$f_{pn}$的集合，其维度为$N\times H\times W\times (C_v+C_l+8)$。

CMSA

由于多模态特征$F$维度大且可能存在很多冗余信息，且$F$的维度取决于语言描述中的词数。
文章提出CMSA模块，能同时利用多模态之间的长距离依赖性，且其输出不依赖于语言描述中的词数。
给定一个特征向量$f_{pn}$，query，key和value分别为其线性变换：
$q_{pn}=W_q{f}_{pn}$,$k_{pn}=W_k{f}_{pn}$和$v_{pn}=W_v{f}_{pn}$，$W_q,W_k,W_v\in {\mathbb{R}}^{512\times (C_v+C_l+8)}$.

cross-modal self-attentive特征 ${\hat{v}}_{p}n$可以表示为：
${\hat{v}}_{pn}={\sum }_{p^{\prime }}{\sum }_{n^{\prime }}{a}_{p,n,p^{\prime },n^{\prime }}{v}_{p^{\prime },n^{\prime }}$
$a_{p,n,p^{\prime },n^{\prime }}=Softmax(q_{p^{\prime },n^{\prime }}^T,k_{p^{\prime },n^{\prime }})$
其中$a_{p,n,p^{\prime },n^{\prime }}$是关于$(p,n)$和另一种组合$(p^{\prime },n^{\prime })$相关性的attention score。

CMSA的最终输出为
$\widehat{f_p}={\text{avg-pool}}_n(W_{\hat{v}}{\hat{v}}_{pn}+f_{pn})=\frac{{\sum }_{n=1}^N(W_{\hat{v}}{\hat{v}}_{pn}+f_{pn})}{N}$
$\hat{F}=\{\widehat{f_p}:\forall p\}$,$\hat{F}\in {\mathbb{R}}^{N\times H\times W\times (C_v+C_l+8)}$
下图为cross-modal self-attentive特征生成过程的示意图

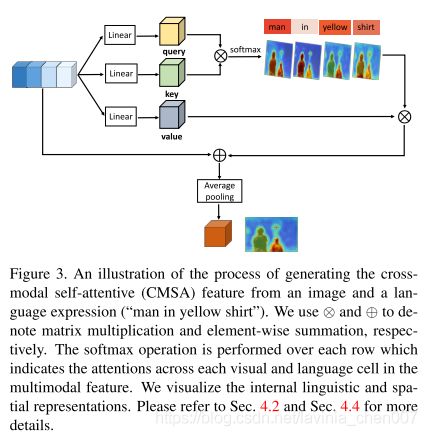
Gated Multi-Level Fusion Module

gated multi-level fusion module用于整合多层级特征。$\widehat{F^{(i)}}$为$i$层的cross-modal self-attentive特征。

对第$i$层，我们生成一个记忆门$m^i$和一个重置门$r^i$（$m^i$，$r^i$ \in ${\mathbb{R}}^{H_i\times W_i}$），类似LSTM中的记忆门和重置门。这些门控制各层中的有多少视觉特征将对最终结果合成的特征做出贡献。

每一层同时还具有一个上下文控制器$G^i$,对其他层流向第$i$层的信息流进行调制。
$G^i=(1-m^i)\odot X^i+{\sum }_{j\in \{1,2,3\}/\{i\}}{\gamma }^j{m}^j\odot X^j$
$F_o^i=r^i\odot \tanh (G^i)+(1-r^i)\odot X^i,\forall i\in \{1,2,3\}$
再通过3x3conv以及sigmoid函数产生最终输出的probability map。

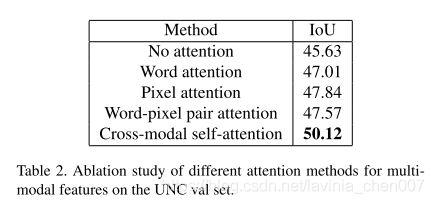
实验结果

在UNC数据集上进行Alation Study结果显示如下
与SOTA方法比较结果显示如下
结果示意

代码笔记

代码通过TensorFlow实现。

特征

空间坐标特征

def generate_spatial_batch(N, featmap_H, featmap_W):
    spatial_batch_val = np.zeros((N, featmap_H, featmap_W, 8), dtype=np.float32)
    for h in range(featmap_H):
        for w in range(featmap_W):
            xmin = w / featmap_W * 2 - 1
            xmax = (w+1) / featmap_W * 2 - 1
            xctr = (xmin+xmax) / 2
            ymin = h / featmap_H * 2 - 1
            ymax = (h+1) / featmap_H * 2 - 1
            yctr = (ymin+ymax) / 2
            spatial_batch_val[:, h, w, :] = \
                [xmin, ymin, xmax, ymax, xctr, yctr, 1/featmap_W, 1/featmap_H]
    return spatial_batch_val

CMSA层

 def cmsa_layer(self, in_feats, name, dim= 512, sub = 2, out_dim = 2008):
        with tf.variable_scope(name):
            theta = tf.layers.conv3d(in_feats, filters= dim, kernel_size= 1, padding='SAME', dilation_rate=(1, 1, 1),  activation= tf.nn.relu, kernel_initializer= tf.contrib.layers.xavier_initializer())
            theta = tf.reshape(theta, [self.batch_size,-1, dim])
            phi = tf.layers.conv3d(in_feats, filters= dim, kernel_size= 1, padding='SAME', dilation_rate=(1, 1, 1),  activation= tf.nn.relu, kernel_initializer= tf.contrib.layers.xavier_initializer())
            phi = tf.layers.max_pooling3d(phi, pool_size = sub, strides=sub, padding='same')
            phi = tf.reshape(phi, [self.batch_size,-1, dim])
            phi = tf.transpose(phi, perm=[0,2,1])
            feat_nl = tf.matmul(theta, phi) # b, thw, thw
            feat_nl = tf.nn.softmax(feat_nl, -1)
   
            feats = tf.layers.conv3d(in_feats, filters= dim, kernel_size= 1, padding='SAME', dilation_rate=(1, 1, 1),  activation= tf.nn.relu, kernel_initializer= tf.contrib.layers.xavier_initializer()) # bthwc
            feats = tf.layers.max_pooling3d(feats, pool_size = sub, strides=sub, padding='same')
            feats = tf.reshape(feats, [self.batch_size,-1, dim])
            feats = tf.matmul(feat_nl, feats)
            feats = tf.reshape(feats, [self.batch_size,-1, 40,40, dim])
            
            feats = tf.layers.conv3d(feats, filters= out_dim, kernel_size= 1, padding='SAME', dilation_rate=(1, 1, 1),  activation= tf.nn.relu, kernel_initializer= tf.contrib.layers.xavier_initializer())
            feats = feats + in_feats 
            
            feats = tf.reduce_mean(feats, axis=1, keep_dims=False)
            return feats

Gated Multi-Level Fusion Module

 def MGATE(self, name, h_feats, l1_feats, l2_feats, c_dim, alpha = 0.5 ):
        with tf.variable_scope(name):
            x1 , x2 , x3 = h_feats, l1_feats, l2_feats # batch h w c
            x1_out = self.GATECell('x1', x1, x2,x3, c_dim, alpha)
            x2_out = self.GATECell('x2', x2, x1,x3, c_dim, alpha)
            x3_out = self.GATECell('x3', x3, x1,x2, c_dim, alpha)
            out = x1_out + x2_out + x3_out
            
            return out

    def GATECell(self, name, x1, x2, x3, c_dim, alpha ):
        with tf.variable_scope(name):
            y = tf.layers.conv2d(x1, filters= c_dim*3, kernel_size= 3, padding='SAME', dilation_rate=(1, 1),  activation= None, kernel_initializer= tf.contrib.layers.xavier_initializer())
            i, f, r = tf.split(y, 3, axis= 3)
            f = tf.sigmoid(f + 1.0) 
            r = tf.sigmoid(r + 1.0) 
            a = tf.Variable(alpha, trainable=True)
            c = a*f*x2 + (1-a)*f*(x3) + (1-f)*i
            out = r * tf.tanh(c) + (1-r)*x1
            return out