西电数据挖掘实验1——二分网络上的链路预测

一、实验内容

  基于网络结构的链路预测算法被广泛的应用于信息推荐系统中。算法不考虑用户和产品的内容特征，把它们看成抽象的节点，利用用户对产品的选择关系构建二部图。为用户评估它从未关注过的产品，预测用户潜在的消费倾向。

  MovieLens是历史最悠久的推荐系统。它由美国Minnesota大学计算机科学与工程学院的GroupLens项目组创办，是一个非商业性质的、以研究为目的的实验性站点。MovieLens主要使用Collaborative Filtering和Association Rules相结合的技术，向用户推荐他们感兴趣的电影。

  数据集：ml-latest-small.zip中包括700个用户对9000部电影的100000条评价。

二、分析及设计

  Step1：采用二分网络模型，对ml-1m文件夹中的“用户-电影”打分数据进行建模

  用户对自己看过的电影打分1-5分，其中1分表示最不喜欢，5分表示最喜欢。假设分数大于3分的，表示用户喜欢这部电影，在二部图中构建一条从用户到该电影的连边。

  考虑由$m$个用户$n$部电影构成的电影推荐系统。若用户$i$对电影$j$打分超过3分，就在$i$和$j$之间连接一条边$a_{ij}=1$，否则$a_{ij}=0$。

  在计算出$a$后，我们首先要处理$a$中无意义的电影列，即去掉那些未被任何用户评价过的电影及编号不存在的电影所在的列。为此，我们要先计算出电影的度矩阵$k\_movie$和用户的度矩阵$k\_user$（同时也便于后续求资源配额矩阵）。找到$k\_movie$中度为0的电影并将其对应的列从$a$中删去即完成了数据预处理。

  数据预处理完成后，我们就可以划分数据集了：随机取$a$中90%的数据构成训练集，剩余10%构成测试集。

  Step2：计算资源配额矩阵

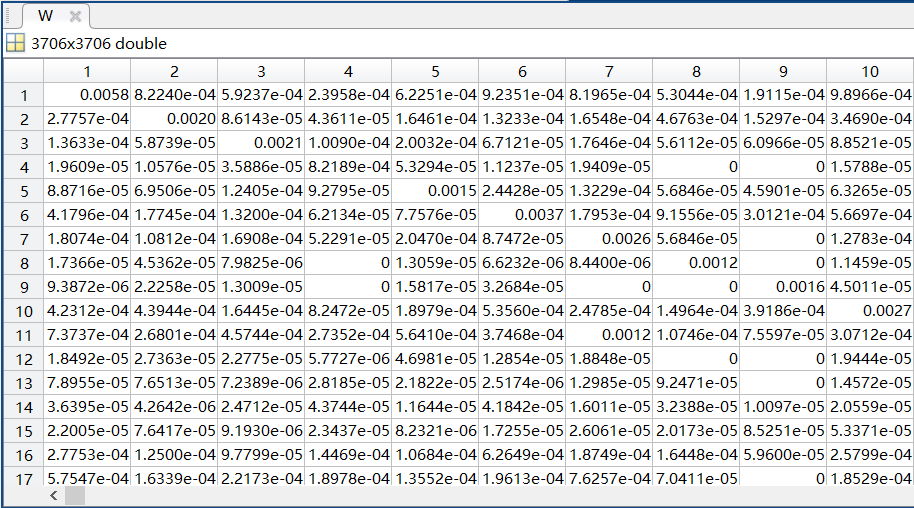
  用训练集数据计算资源配额矩阵$W$。$W$中的元素$w_{ij}$表示产品$j$愿意分配给产品$i$的资源配额（假设一个用户选择过的产品$j$都有向该用户推荐其他产品$i$的能力）。$w_{ij}$的计算公式如下：
$$w_{ij}=\frac{1}{k_j}\sum _{l=1}^m\frac{a_{li}{a}_{lj}}{k_l}$$
其中$k_j$表示产品$j$的度（被多少用户评价过），表示$k_l$用户$l$的度（评价过多少产品）。

  在计算$W$时，若采用三重循环的方式进行计算，则复杂度将达到$O(m{n}^2)$，计算耗时太长，所以在这里我采用了矩阵乘法加快运算。具体做法是先对矩阵$a$的第$j$列除以$k\_movie(j)$，再对$a$的第$i$行除以$k\_user(i)$，最后用得到的矩阵与$a$进行矩阵乘法即可得到矩阵$W$，具体实现见下文代码。

  Step3：对于目标用户，按照其喜欢程度，对电影进行排名，进行电影推荐

  我们对测试集中的用户进行电影推荐。设目标用户的资源分配矩阵为$f$。初始时，将各用户喜欢的电影的对应项资源设置为1，其他为0，即可得到尺寸为$n\times n$的0/1矩阵。将$f$与资源配额矩阵$W$相乘，得到最终的资源分配矩阵:
$$f^{\prime }=Wf$$
  将用户所有没看过的电影按照$f^{\prime }$中对应项的得分进行降序排列，将排名靠前的电影推荐给目标用户。

  Step4：计算r值量化评价算法的精确度

  对给定用户$i$，假设他对$L_i$个电影的评分≤3，如果在测试集中用户$i$喜欢了电影$j$（打分＞3），而电影$j$依据向量$f^{\prime }$被排在第$R_{ij}$位，定义该电影的相对位置：
$$r_{ij}=\frac{R_{ij}}{L_i}$$
  越精确的算法，给出的$r_{ij}$越小。对所有用户的$r_{ij}$求平均值$r\_score$来量化评价算法的精确度。

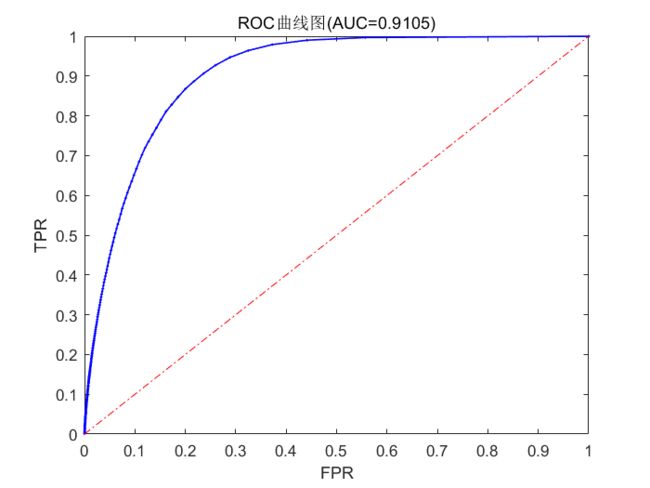
  Step5：绘制ROC曲线并计算AUC衡量算法的预测准确性

  将$f^{\prime }$矩阵中的电影推荐评分从高到低降序排列，依次选取不同的电影推荐得分作为阈值，计算测试集中所有用户对应的TP、FP、TN、FN值并进一步求出各自的FPR、TPR值。求出这些用户的FPR均值、TPR均值作为ROC曲线上的一对(FPR,TPR)值，最终绘制出ROC曲线。在绘制出ROC曲线后，我又采取了近似算法计算了AUC以更为直观地对不同的ROC曲线进行比较。

三、详细实现

  考虑到本次实验有很多关于矩阵的运算，而Matlab的Workplace能提供运算过程中各变量信息、内容的实时查看，便于我们对照Workplace检查各矩阵的尺寸、值是否正确无误，因此我使用Matlab编写了本次实验的程序。具体代码实现如下（所有重要语句均已给出相应的注释）：

1.读取ratings评分文件，然后提取主要信息，并计算出用户数、电影数：

clear;
close all;
% 读取评分文件
ratings = dlmread('C:\Users\HP\Desktop\数据挖掘上机作业\ml-1m\ratings.dat');
% 我们只需要提取用户、电影、评分这3列
ratings = ratings(:, [1,3,5]);
% 求用户数及总电影数
user_num = max(ratings(:,1));
movie_num = max(ratings(:,2));

2.计算二部图邻接矩阵，若用户对电影的评分大于3，则在二部图中添加一条对应的边：

% 初始化二部图邻接矩阵a
a = zeros(user_num,movie_num);
for i = 1 : user_num
    % 找到所有第一列值为i的行号
    temp_index = find(ratings(:,1)==i);
    % 取出第一列值为i的所有行放入temp矩阵
    temp = ratings(temp_index,:);
    for j = 1 : length(temp_index)
        % 若评分大于3，则在二部图中添加一条对应的边
        if temp(j,3) > 3
            a(i,temp(j,2)) = 1;
        end
    end
end

3.计算用户和电影的k值：

% 初始化用户k值和电影k值
k_user = zeros(user_num,1);
k_movie = zeros(movie_num,1);
% 计算用户k值
for i = 1 : user_num
    k_user(i) = length(find(ratings(:,1)==i));
end
% 计算电影k值
for i = 1 : movie_num
    k_movie(i) = length(find(ratings(:,2)==i));
end

4.清理噪声数据，然后划分训练集和测试集，计算训练集和测试集各自对应的用户k值：

% 先通过k_movie找出所有未被任何一个用户评价过的电影，清理噪声数据
bad_index = find(k_movie == 0);
a(:,bad_index) = [];
k_movie(bad_index) = [];
[~,movie_num] = size(a);

% 划分数据集：90%作为训练集，10%作为测试集
test_num = round(user_num * 0.1);
train_num = user_num - test_num;
% 随机抽取a矩阵中10%的行出来构成测试集
rand_idx = randperm(user_num);
test_index = rand_idx(1:test_num);
a_test = a(test_index,:);
a(test_index,:) = [];
% a中剩下的90%的行构成训练集
a_train = a;
% 计算训练集和测试集中的用户k值
k_user_test = k_user(test_index,:);
k_user(test_index,:) = [];
k_user_train = k_user;

5.根据公式计算资源配额矩阵W：

% 利用训练集计算资源分配矩阵W
% 初始化计算需要用到的临时矩阵
temp1 = zeros(train_num,movie_num);
temp2 = zeros(train_num,movie_num);
% 先对a_train的列进行除操作
for i = 1 : movie_num
    temp1(:,i) = a_train(:,i) / k_movie(i);
end
% 再对a_train的行进行除操作
for i = 1 : train_num
    temp2(i,:) = temp1(i,:) / k_user_train(i);
end
% 由矩阵乘法得到W，加速计算过程
% W是n×n矩阵
W = a_train' * temp2;

6.在测试集上计算推荐评分矩阵f，然后计算r矩阵，最后计算出衡量算法准确度的r值：

% -------------下面是测试集运算---------------------%
% 用测试集计算推荐评分矩阵f，尺寸为test_num×movie_num
f = (W * a_test')';
% 初始化R矩阵，第i行存放对于用户i，这些电影中的每个电影在评分中的排名
R = zeros(test_num,movie_num);
% 初始化r矩阵
r = zeros(test_num,movie_num);
% 计算R矩阵
for i = 1 : test_num
    [~,R(i,:)] = sort(f(i,:), 'descend');
end
% 计算r矩阵
for i = 1 : test_num
    % r(i,:) = R(i,:) / (movie_num - k_user_test(i));
    r(i,:) = R(i,:) / (movie_num - sum(a_test(i)));
end
% 计算r值，衡量模型准确度
r_score = mean(r(:));

7.最后，计算TP,TN,FP,FN，然后求出FPR,TPR并绘制ROC曲线，求出AUC值：

% 最后一步，绘制ROC曲线
% 设置阈值分别为0-1.4中间的若干个数
% 定义最大循环次数
max_epoch = 5000;
% 初始化x,y向量，存放每个阈值下对应的fpr和tpr
x = zeros(1,max_epoch);
y = zeros(1,max_epoch);
% count记录循环次数
count = 1;
for t = 0 : 0.001 : 1.4
    % 初始化pred矩阵，代表当前阈值下的推荐电影(预测)矩阵
    pred = double(f >=t);
    % fact矩阵是真实矩阵，代表用户真实喜欢的电影
    fact = a_test;
    % 下面计算TP TN FP FN矩阵(尺寸为600×1)
    TP = sum(double((pred == 1) & (fact== 1)),2);
    FP = sum(double((pred == 1) & (fact== 0)),2);
    TN = sum(double((pred == 0) & (fact== 0)),2);
    FN = sum(double((pred == 0) & (fact== 1)),2);
    % 计算FPR TPR矩阵
    FPR = FP ./ (FP + TN);
    TPR = TP ./ (TP + FN);
    % 对各用户的FPR TPR求均值，得到一个阈值下最终的FPR和TPR
    fpr = mean(FPR);
    tpr = mean(TPR);
    x(count) = fpr;
    y(count) = tpr;
    count = count + 1;
end

% 近似计算AUC值
AUC = 0;
for i = 2 : length(x)
    AUC = AUC + (x(i-1) - x(i)) * y(i-1);
end
disp(AUC);

% 绘制ROC曲线图
plot(x,y,'-bo','LineWidth',1,'MarkerSize',1);
xlabel('FPR');
ylabel('TPR');
title(sprintf("ROC曲线图(AUC=%.4f)", AUC));
hold on;
line([0,1],[0,1],'linestyle','-.','color','r');

四、实验结果

• 资源配额矩阵$W$部分内容展示：

• 电影评分矩阵$f$部分内容展示：

• 算法的$r=0.5002$，说明模型预测的结果比较准确：

• ROC曲线：

五、心得体会

  1. 一开始我在计算$W$时用三重循环，发现跑了很长时间才算出结果（344.5秒），后来在纸上推导了一下矩阵运算步骤，把用循环计算$w_{ij}$的过程转换为了矩阵相乘的操作，极大地提升了运算速度（1.87秒）。

  2. 一开始我在计算得到$W$后，检查$W$值，发现其中有部分列为全$NAN$，这会影响后续计算矩阵$f$。分析数据集可知有部分电影编号并未出现在1-3952中，也有部分电影并未被任何一个用户评价过，而这部分电影会影响后续计算。在发现这一点后，我先在矩阵$a$中去除了这些电影对应的列，再计算$W$，最终得到正确结果。

  3. 在计算$r$时，实验文档中写的一句话是“如果在测试集中用户$i$选择了电影$j$”。我认为，对于这其中的“选择”有两种理解，一种是该用户仅仅评论过该电影，另一种是该用户喜欢了该电影（即打分＞3）。若从不同的理解出发去算$r$值和后续的ROC曲线，会有一些不同之处。为了进行充分的对比说明，我又进行了对照实验，结果如下：

认为“选择”是评价过电影

认为“选择”是喜欢了电影

  可以发现，若认为用户选择了电影仅是评价过电影，则计算出的r值较大(0.5254)，若认为用户选择了电影是用户喜欢了电影，即对电影的评分＞3，则计算出的r值较小(0.5002)，即算法的精确性更高。而两者在ROC曲线及其AUC值上的表现并没有明显的区别。