《融合TangentBug与Dubins曲线的智能轮式车辆局部路径规划算法》论文解读一

本文参考Bug算法(Bug Algorithms)简介（Bug1 & Bug2 & Tangent Bug）_nullwh的博客-CSDN博客_bug算法

原始书籍(PDF) Principles of Robot Motion: Theory, Algorithms, and Implementation ERRATA!!!! 1 (researchgate.net)

这篇论文主要利用TangentBug与Dubins曲线进行轨迹规划，下面先介绍TangentBug算法的具体细节，以便对论文的理解

目录

1 Bug类算法

1.1 Bug1算法

1.2 Bug2算法

2 TangentBug算法

2.1 算法的改进

2.2 算法具体细节

2.2.1算法过程

2.2.2 启发式距离的设定

2.2.3 重规划

2.2.4 切换运动方式的最短距离

​2.2.5 算法伪代码

​2.3 激光雷达半径对算法的影响

3 Dubins曲线

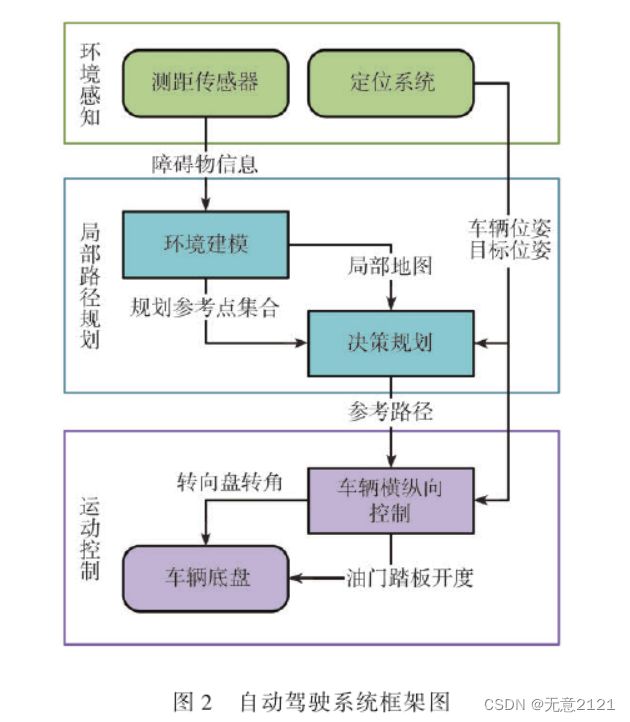
4 论文自动驾驶系统框架

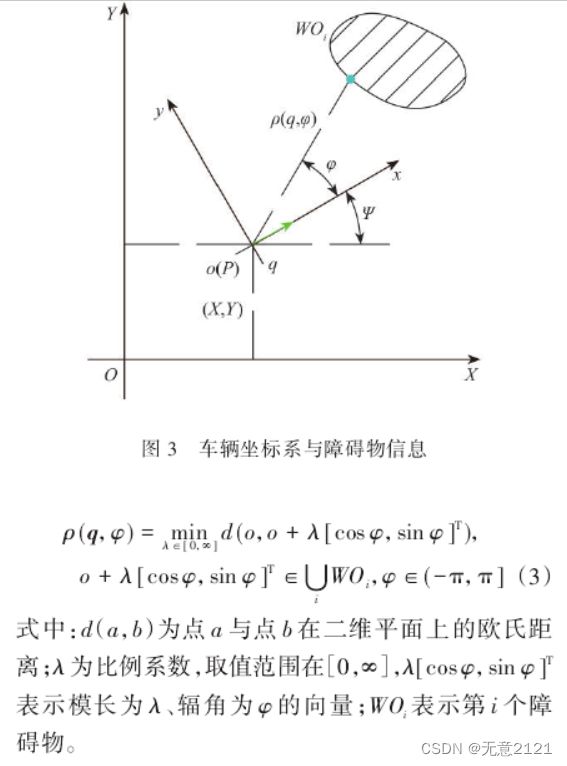
5 环境建模

---

1 Bug类算法

智能仿生类算法参考了生物的行为模式和特性，其中Lumelsky等人参考爬虫（Bug）的行为模式，针对仅能获取局部地图和定位信息的情况，提出了Bug1算法和Bug2算法。

1.1 Bug1算法

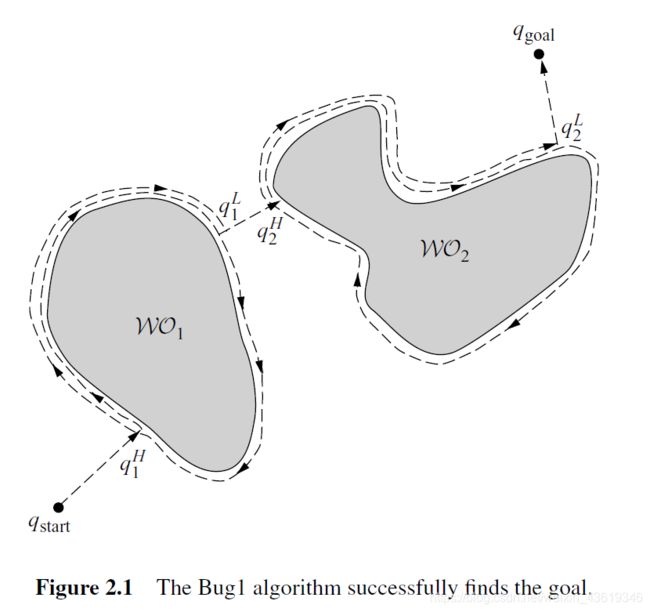
该算法核心思想是在没有障碍物时，沿着从当前位置向目标运动的直线可以得到最短的路线。当传感器检测到障碍物时，机器人绕行障碍物一圈检测出障碍物的边界离目标最近的位置，再从该位置出发。

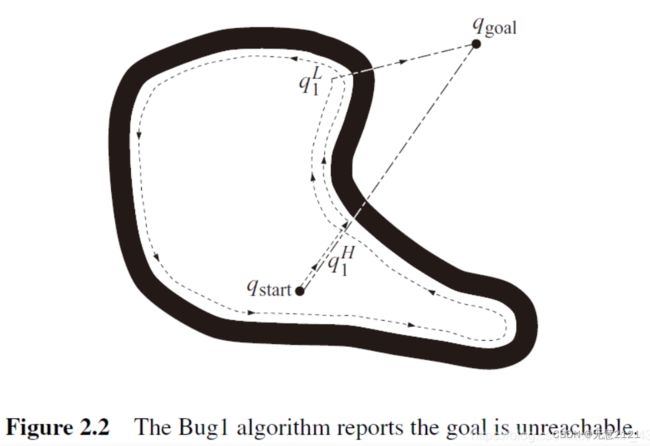
 如图2.1所示，起始点和目标点分别为qstart 和qgoal，令qL0 = qstart 。当前位置是qLi-1，并称连接qLi-1 和 qgoal的线段为最新的m-line. 没有遇到障碍时，机器人沿着m-line朝目标qgoal直线移动. 如果遇到障碍，则称点qHi为第 i 次遇到障碍时的撞击点（hit point）. 接着，机器人环绕障碍物移动直至返回 qHi点。然后判断出障碍物边界上离目标最近的点，并移到这个点上，该点称为离开点（leave point），由 qLi表示。从qLi开始机器人再次沿直线驶向目标，如果这条线与到最近障碍物的距离过短，则不存在到达目标的路径，如图2.2，否则继续重复上述步骤。但是Bug1算法的效率很低，绕行障碍物一圈耗费过多时间，但可以保证机器人能到达任何可达的目标，具有概率完备性。

伪代码如下

1.2 Bug2算法

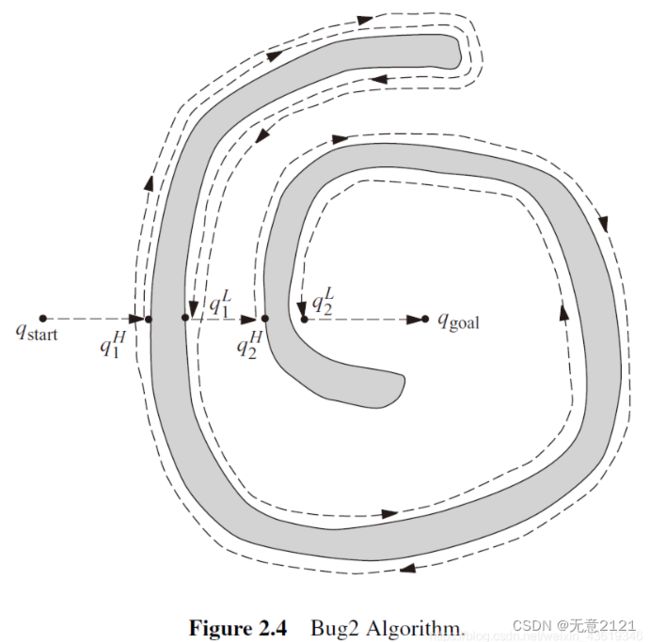
Bug2算法与Bug1算法最大的区别是m-line没有实时更新，Bug2始终认为出发点到目标点的方向是最短路径的方向，而Bug1认为当前障碍物边界离目标点最近的方向是最短路径的方向。所以Bug2算法中的机器人会在环绕障碍物的时候，判断是否回到了m-line上，一旦回到那条直线就再次沿着直线运动。假如回到了撞击点，那么意味着不能到达目标点。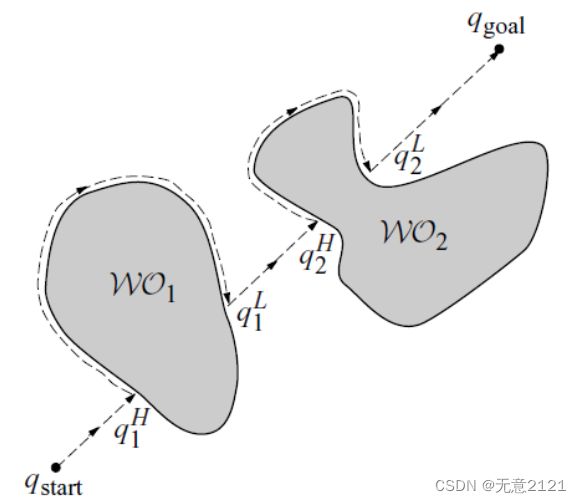

伪代码如下

对于一般的环境，Bug2算法的效率更高；而对于复杂形状的障碍物，保守的Bug1算法性能却更优。Bug2算法也有缺陷的地方，如图2.4所示的螺旋形障碍物，Bug2算法会得到过长的路径。

 

2 TangentBug算法

2.1 算法的改进

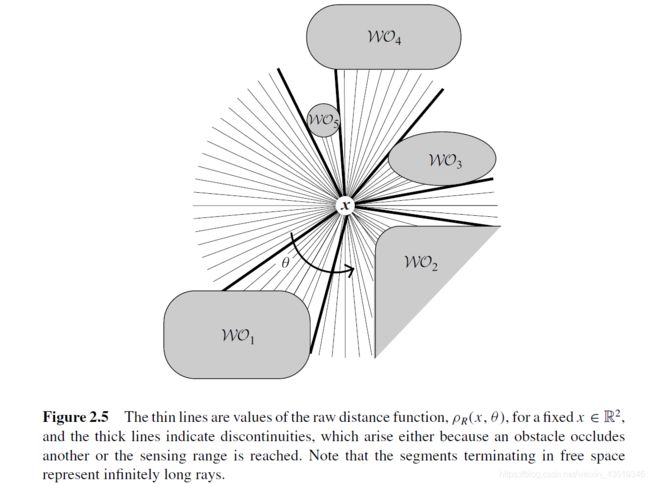
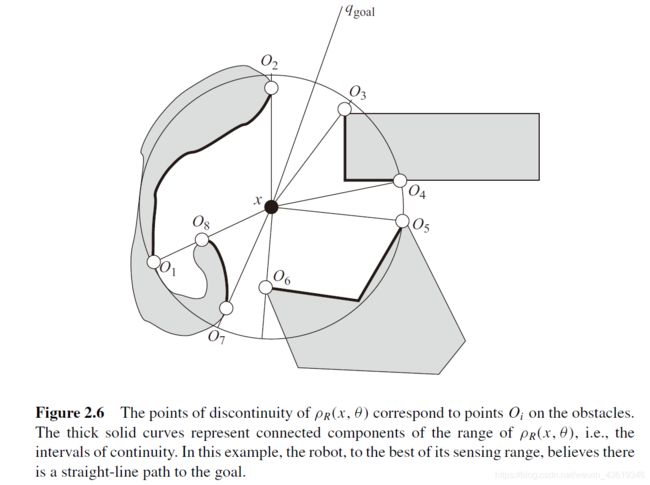
TangentBug算法是对Bug2算法的改进。它利用机器人上距离传感器的读数对障碍物做出提前规避，可以获得更短更平滑的机器人路径。假设机器人上安装有360°激光雷达(或者红外距离传感器),传感器检测的范围有限，因此有一个最大距离。那么我们可以测得每束光线到达障碍物的距离。细线代表发出的红外线,粗线代表了红外线被遮挡(说明机器人无法到达这些位置)。

并对障碍物边界离当前位置的距离连续变化的范围进行标记，下面我都称其为临界点，如图2.6，O1到O2之间障碍物边界到当前位置的距离连续变化，O1与O2这两个点都会发生突变，这些临界点就是机器人避开障碍物的关键

2.2 算法具体细节

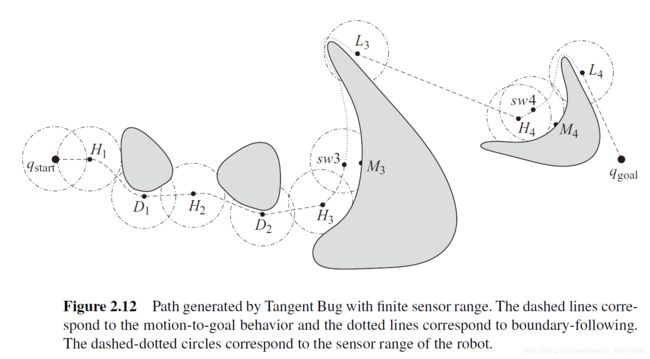
2.2.1算法过程

（1）沿着初始位置向目标位置的方向前进

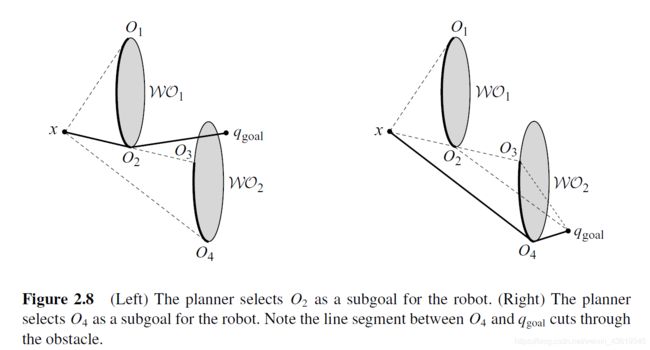
（2）当激光雷达检测到障碍物，对临界点进行标记，并计算临界点的启发式距离，比较这些临界点的启发式距离，朝着启发式距离最小的临界点前进

（3）以一定时间间隔更新临界点，从而动态调整速度方向，使得最后的轨迹较平滑

2.2.2 启发式距离的设定

启发式距离是人为规定的，论文中选择 d(x,Oi)+d(Oi,qgoal)

2.2.3 重规划

临界点是实时更新的，这将导致最后机器人靠近障碍物时行走的轨迹是一条曲线而不是直线，从而更符合机器人的运动学规律，为控制模块服务。

2.2.4 切换运动方式的最短距离

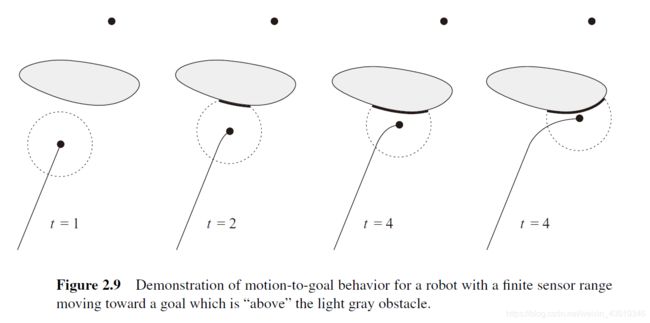
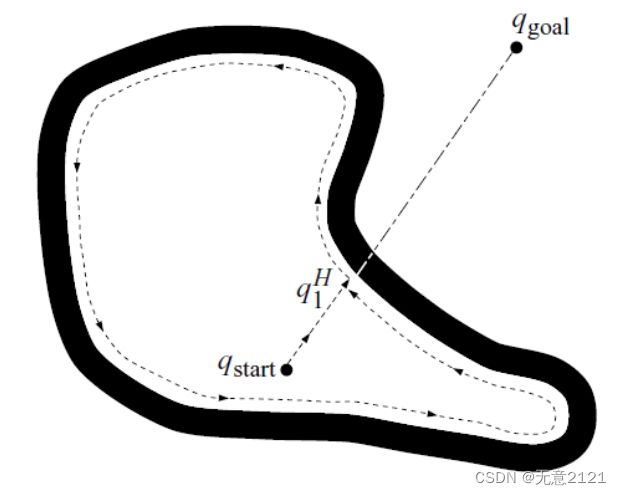
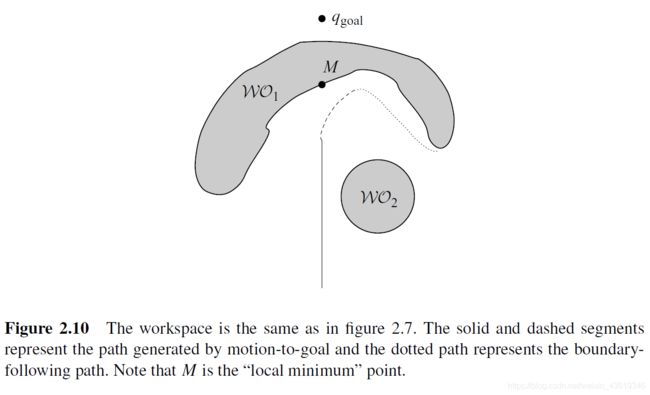
当离最近障碍物的距离小于一定值时，就需要将向临界点移动的运动方式切换为环绕障碍物运动。如下图 M 点是机器人探索距离小于临界值，M 点成为在障碍物边界上的局部极小点。机器人开始沿着障碍物边界进行环绕，图中虚线路径就是机器人环绕障碍物时所走的路径。当机器人探测到临界点里目标点的距离比 M 点更小时，重新开始接近目标的运动。

2.2.5 算法伪代码

2.3 激光雷达半径对算法的影响

 当激光雷达的检测半径是0时，TangentBug算法就退化成了Bug2算法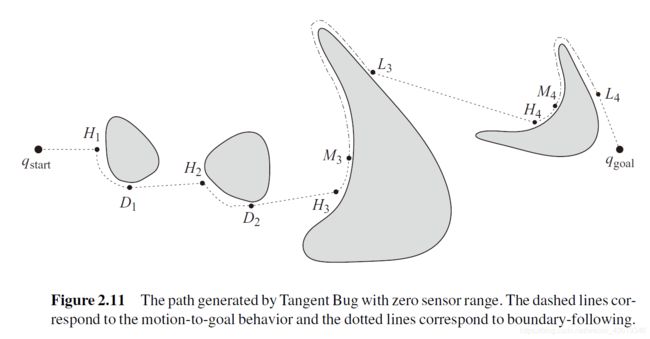

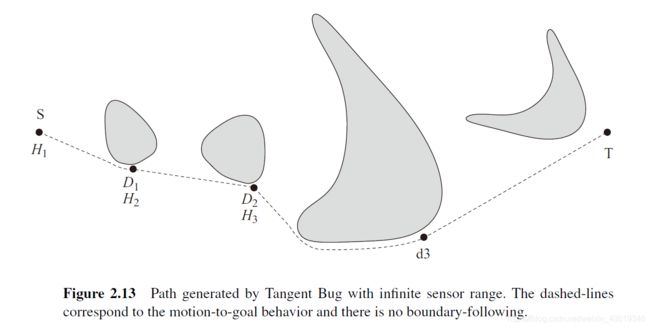
当激光雷达的检测半径到达无穷时，机器人将不再环绕障碍物，而是始终朝着启发式距离最小的临界点前进，这样规划出来的路径非常短

3 Dubins曲线

Dubins曲线更符合轮式车辆的运动学规律，通过TangentBug算法与Dubins曲线的融合，使得应用于全向移动机器人的算法TangentBug也能应用于智能车轨迹规划。关于Dubins曲线的细节，请参考【自动驾驶轨迹规划之dubins曲线与reeds-shepp曲线】_无意2121的博客-CSDN博客_车辆轨迹规划

4 论文自动驾驶系统框架

通过测距传感器得到障碍物的边界信息，通过定位系统得到车辆当前位置的位姿和目标点的位姿，再利用论文中提出的决策规划算法得到参考路径，并将参考路径传递到运动控制模块进行路径跟踪。

 

5 环境建模

 

但实际的传感器有一定分辨率，障碍物信息一定是离散的，同时传感器由一定的检测范围。因此，我们需要重新定义障碍物信息。

注意车辆坐标系与世界坐标系的转换。下一篇文章将详细介绍融合TangentBug算法与Dubins曲线的决策规划的具体细节