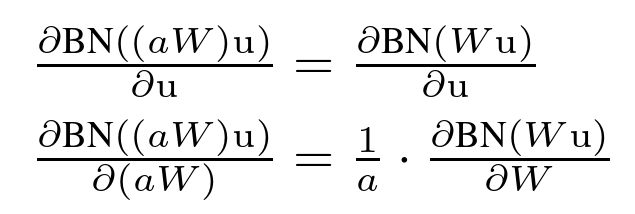经典BN很NB,精读论文《Batch Normalization》
Batch Normalization: Accelerating Deep Network Training byReducing Internal Covariate Shift
《批量标准化:通过减少内部协变量的偏移加速深度网络训练》
首先看摘要和结论,然后分析核心思想,最后总结表格内容和实验细节。
目录
一、摘要
二、结论
三、通过小批量统计实现批标准化
(1)标准化随机变量
(2)批标准化(BN)***
(3)训练一个BN网络 ***
四、BN网络的学习率和正则化
(1)Batch-Normalized Convolutional Networks
(2)Batch Normalization enables higher learning rates
(3)Batch Normalization regularizes the model
五、加速BN网络
六、Inception和不同BN网络之间的性能对比
七、GoogleNet_v1 和 GoogleNet_v2(BN) 模型结构的比较
一、摘要
训练深度神经网络是一个复杂的事实,在训练过程中每一层的输入分布随着前一层的参数变化而变化。这就需要较低的学习速率和仔细的参数初始化来减缓训练速度,并且使得具有饱和非线性的模型的训练变得非常困难。我们将这一现象称为内部协变量偏移(internal covariateshift),并通过归一化层输入来解决这个问题。我们的方法从将规范化作为模型架构的一部分和对每个训练小批量执行规范化来吸取其优点。Batch Normalization允许我们使用更高的学习速率,对初始化不那么小心。它还起到正则化的作用,在某些情况下消除了Dropout的需要。应用于一种SOTA的图像分类模型,Batch Normalization以14倍的训练步数达到了同样的精度,并且大大超过了原模型。使用Batch Normalization网络集合,我们对ImageNet分类的最佳公布结果进行改进:达到top-5的4.9 %的验证误差( 4.8 %的测试误差),超过了人类评分者的准确率。
++++++++++++++++++名词解释++++++++++++++++++
协变量:在实验的设计中,协变量是一个独立变量(解释变量),不为实验者所操纵,但仍影响实验结果。
内部协变量偏移:在神经网络模型的训练过程中产生的协变量,因为层数多的缘故逐渐发生偏移。而这种偏移会大大影响网络的训练,所以我们需要把内部协变量拉回正轨。
BN==批标准化==批规范化==批归一化
二、结论
我们提出了一种新的机制来大大加快深度网络的训练。它是基于协变量偏移这一已知使机器学习系统训练复杂化的前提,也适用于子网络和层,将其从网络内部激活中剔除可能有助于训练。我们提出的方法从标准化激活中汲取其力量,并将这种标准化纳入网络体系结构本身。这确保标准化通过用于训练网络的任何优化方法得到适当处理。为了使深度网络训练中常用的随机优化方法得以实现,我们对每个小批量进行归一化处理,并通过归一化参数反推梯度。批标准化每次激活只增加两个额外的参数,这样做保持了网络的表示能力。我们提出了一种用批归一化网络构造、训练和执行推理的算法。所得到的网络可以用饱和的非线性项进行训练,对增加的训练速率更容忍,并且通常不需要Dropout进行正则化。
仅仅将批处理规范化添加到一个先进的图像分类模型中,就会在训练中获得大幅度的加速。通过进一步增加学习速率、删除Dropout以及应用Batch Normalization所做的其他修改,我们只需少量的训练步骤就可以达到之前的state of the art,然后在单网络图像分类中击败state of the art。此外,通过将多个模型与批处理规范化训练相结合,我们的性能比ImageNet上最著名的系统要好,有很大的优势。
有趣的是,我们的方法与《Knowledge matters: Importance of prior information for optimization》的标准化层有相似之处,认为两种方法源于非常不同的目标,执行不同的任务。批正规化的目标是通过训练实现激活值的稳定分布,在我们的实验中,我们将其应用于非线性之前,因为在非线性之前,匹配第一和第二时刻更容易导致稳定分布。相反,《Knowledge matters: Importance of prior information for optimization》将标准化层应用于非线性度的输出,从而导致更稀疏的激活。在我们的大规模图像分类实验中,我们没有观察到非线性输入是稀疏的,也没有没有进行批量归一化。Batch Normalization的其他显著区分特性包括允许BN变换表示身份的学习尺度和移位、卷积层的处理、不依赖于小批量的确定性推理以及网络中每个卷积层的批规范化,而标准化层并没有要求这样做,因为它之后是学到的线性转换形式,从概念上来说,吸收了必要的尺度和移位。
在这项工作中,我们没有探讨批量标准化可能允许的所有可能性。我们未来的工作包括将我们的方法应用于递归神经网络《On the difficulty of training recurrent neural networks》,其中内部协变量的偏移和消失或爆炸的梯度可能特别严重,这将使我们能够更彻底地检验归一化改善梯度传播的假设(批量标准化使学习率更高)。我们研究批量标准化是否有助于传统意义上的领域适应,即网络进行的归一化是否会使其更容易地泛化到新的数据分布中,也许只是对种群均值和方差的重新计算(训练一个批量归一化网络,12个步骤)。最后,我们认为,对该算法进行进一步的理论分析将允许更多的改进和应用。
我们将内部协变量移位定义为:训练过程中由于网络参数的变化而引起的网络激活分布的变化。为了改进训练,我们寻求减少内部协变量的偏移。通过固定层输入 x 的分布随着训练的进行,我们期望提高训练速度。
三、通过小批量统计实现批标准化
(1)标准化随机变量
标准化随机变量(standardized random variable)亦称“规范随机变量”。数学期望(均值)为 0 和方差等于 1 的随机变量。
标准化随机变量是指经过处理,从而具有一些较好性质的随机变量。设 X* 为随机变量,则称
为标准化随机变量。这时,E(X*)=0, D(X*)=1。
(2)批标准化(BN)***
在每个训练步都以整个训练集为基础的 batch 设置中,我们将使用整个训练集对激活进行归一化处理。然而,这在使用随机优化时是不切实际的。因此,我们做了第二个简化:由于我们在随机梯度训练中使用了小批量,因此每个小批量产生了对每个激活的均值和方差的估计。这样,用于归一化的统计量就可以完全参与梯度反向传播。
输入:一个小批量的值:B={x1...m}; 可学习的参数:![]() 、
、![]()
- 小批量 B 的平均值,得到
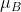
- 小批量 B 的方差

- 通过第一步和第二步得到的
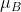 和
和  对 B 进行规范化,得到
对 B 进行规范化,得到 
- 对规范化后得到的
 进行缩放和平移操作,得到最终的输出结果
进行缩放和平移操作,得到最终的输出结果 
其中,![]() 是小批量批量方差的常数,用于数值稳定性。
是小批量批量方差的常数,用于数值稳定性。
图1 BN变换算法,应用于小批量上的激活 x
(3)训练一个BN网络 ***
忽略 ![]() ,这些归一化激活具有与训练时相同的均值0和方差1。我们使用无偏方差估计
,这些归一化激活具有与训练时相同的均值0和方差1。我们使用无偏方差估计![]() ,其中期望是大小为 m 的经过训练的小批量,
,其中期望是大小为 m 的经过训练的小批量,![]() 是它们的样本方差。用移动平均值代替,我们可以跟踪模型训练时的精度。由于在推理过程中,均值和方差是固定的,因此归一化只是一个线性变换应用于每个激活。它可能进一步与
是它们的样本方差。用移动平均值代替,我们可以跟踪模型训练时的精度。由于在推理过程中,均值和方差是固定的,因此归一化只是一个线性变换应用于每个激活。它可能进一步与 ![]() 的缩放和
的缩放和 ![]() 的移位组成,从而产生替代 BN(x) 的单一线性变换。下面的步骤总结了BN网络的训练过程。
的移位组成,从而产生替代 BN(x) 的单一线性变换。下面的步骤总结了BN网络的训练过程。
输入:具有可训练参数 ![]() 的网络 N ;激活的子集
的网络 N ;激活的子集 ![]()
输出:应用于推理的批量标准化网络 ![]()
- 训练BN网络,即把普通N训练成
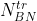
- 开始循环K次
- 把BN算法得到的变形的结果
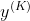 添加到
添加到 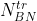 中
中 - 用输入
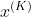 修改
修改 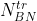 中的每一层,修改的方法:取
中的每一层,修改的方法:取 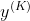 代替
代替 - 循环K次,遍历所有的激活子集
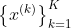 中的所有
中的所有 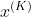 后,结束循环
后,结束循环 - 训练
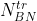 用于优化参数:
用于优化参数: ∪
∪ 
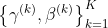
- 具有冻结的参数的推断BN网络,即
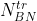 过渡到
过渡到 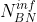
(优化的参数冻结,即用具有冻结参数的BN网络去做预测) - 开始循环K次
- 为了方便观察,令
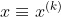 ,
, 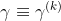 ,
, 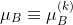 , 等
, 等 - 加工处理多个训练的小批量 B,每一个 B 的大小为 m,并且对 B 的平均值和方差进行平均化
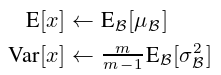 ,得到 E[x] 和 Var[x]
,得到 E[x] 和 Var[x] - 在
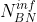 中,用
中,用  来代替BN算法的
来代替BN算法的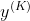
- 循环K次后,结束循环
图2 训练一个BN网络
四、BN网络的学习率和正则化
(1)Batch-Normalized Convolutional Networks
批规范化可以应用于网络中的任意一组激活。这里,我们关注的是由仿射变换和元素非线性组成的变换:
z = g ( W u + b )
其中,W 和 b 是模型的学习参数,函数 g(x) 是 sigmoid 或 ReLU 等非线性项。该公式涵盖了全连接层和卷积层。我们在非线性之前立即加入BN变换,通过归一化 x = Wu + b。我们也可以对层输入 u 进行归一化处理,但由于 u 很可能是另一个非线性的输出,在训练过程中其分布的形状很可能会发生变化,约束其第一、第二时刻并不能消除协变量的偏移。相比之下,W u + b 更可能具有对称的、非稀疏的分布,即 “more Gaussian” ;规范化很可能产生分布稳定的激活。
注意,由于我们对 W u + b 进行了归一化处理,因此可以忽略偏差 b,因为其影响将被后续的均值减法所抵消(偏置的作用由 BN变换算法 中的 β 相加),于是,z = g ( W u + b )替换为
z = g ( BN ( W u ) )
其中BN变换独立地应用于 x = W u 的每个维度,每个维度有一对独立的学习参数 ![]() ,
,![]() 。
。
我们在特征图上学习了一对参数 ![]() 和
和 ![]() ,而不是每次激活。三(3)也做了类似地修改,这样在推理过程中,BN变换对给定特征图中的每个激活都施加相同的线性变换。
,而不是每次激活。三(3)也做了类似地修改,这样在推理过程中,BN变换对给定特征图中的每个激活都施加相同的线性变换。
(2)Batch Normalization enables higher learning rates
在传统的深度网络中,过高的学习速率可能导致梯度的爆发或消失,以及陷入较差的局部极小点。批量标准化有助于解决这些问题。通过对整个网络的激活进行标准化,它可以防止参数的微小变化放大成梯度中激活的较大和次优变化;例如,它防止了训练陷入非线性的饱和状态。
批处理规范化也使训练对参数规模更具弹性。通常情况下,较大的学习速率会增大层参数的尺度,进而放大反向传播过程中的梯度,导致模型爆炸。但是,随着Batch Normalization的进行,通过一层的反向传播不受其参数的尺度影响。的确,对于一个标量 a,有
BN ( W u ) = BN ( ( aW ) u )
求导(梯度传播)如下:
可见尺度不影响梯度传播。此外,较大的权重会导致较小的梯度,批量归一化会稳定参数的增长。
(3)Batch Normalization regularizes the model
使用批处理规范化进行训练时,可以将一个 training example 与 mini-batch 中的其他样本一起看到,训练网络不再为给定的 training example 生成确定性值。在我们的实验中,我们发现这种效应有利于网络的泛化。Dropout《Dropout:A simple way to prevent neural networks from overfit-ting》通常用于减少过拟合,但在批处理标准化网络中,我们发现它可以删除,也可以减少强度。
五、融合BN的普通神经网络
为了验证内部协变量移位对训练的影响,以及Batch Normalization对抗这种影响的能力,我们考虑了MNIST数据集上的数字类预测问题。我们使用了一个非常简单的网络,以28x28的二值图像作为输入,3个全连接的隐藏层,每个激活100个。每个隐层采用Sigmoid非线性计算y = g ( W u + b ),权值W初始化为小随机高斯值。最后一个隐藏层是一个完全连接的层,有10个激活(每类一个)和交叉熵损失。我们对网络进行了50000步的训练,每小批60个例子。我们在网络的每个隐藏层中添加了批量规范化,就像训练一个 BN 神经网络一样(三(3))。我们感兴趣的是 baseline 网络和 BN 网络的比较,而不是在 MNIST 上实现 SOTA 。
图3 有、无BN的神经网络的性能对比
图3(a)受过批量规范化和不受批量规范化训练的MNIST网络的测试精度,与训练步数的关系。批量规范化有助于网络训练更快,达到更高的精度。
图3(b、c)我们展示了每个网络最后一个隐藏层的一个典型激活,它的分布是如何演化的。原始网络中的分布随着时间的推移,无论是均值还是方差都发生了显著的变化,这使得后续各层的训练变得复杂。相比之下,批量规范化网络中的分布比训练过程更稳定,有助于训练。
总结:融合BN的普通网络比没有融合BN的普通网络更快!更稳!
五、加速BN网络
仅仅在网络中加入批正规化并不能充分利用我们的方法。为此,我们进一步改变了网络及其训练参数,如下所示:
- 提高学习率。在批处理标准化模型中,我们已经能够从较高的学习速率中获得训练加速,没有不良的副作用
- 移除Dropout。如四(3)所示,Batch Normalization 完成了与 Dropout 相同的一些目标。从改进的BN-Inception中移除掉Dropout加速训练,而不增加过拟合。
- 减少L2Weight正规化。而在Inception中,模型参数上的L2损失控制了过拟合,在Modified BN-Inception中,这种损失的权重降低了5个因子。我们发现,这提高了对剔除验证数据的准确性。
- 加快学习速率衰减。在训练Inception时,学习速率呈指数衰减。由于我们的网络训练速度快于Inception,所以我们将学习速率降低了6倍。
- 当Inception和其他网络从中受益时,删除局部响应规范化,我们发现使用批量规范化是不必要的。
- 训练样本随机的更彻底。我们启用了对训练数据的碎片化处理,从而避免了相同的示例总是出现在一个小批量的集合中。这使得验证精度提高了约1 %,这与批正规化作为正规化器的观点是一致的:我们方法中所固有的随机占有率在每次看到它对一个例子的影响不同时,应该是最有益的。
- 减少光度畸变。由于批处理标准化网络训练速度更快,观察每个训练示例的次数更少,我们通过更少地扭曲这些“真实”图像,让训练者关注更多的“真实”图像。
六、Inception和不同BN网络之间的性能对比
我们评估了以下网络,所有训练数据都是基于 LSVRC2012 的训练数据,并在验证数据上进行了测试:
- Inception:GoogLeNet网络中的模块,以0.0015的初始学习率进行训练。
- BN-Baseline:在每个非线性之前融合BN的Inception网络。
- BN-x5:融合BN的Inception网络和(四)中的修改操作。并且初始学习率提高了5倍,达到0.0075。相同的学习率随着初始Inception的增加而增加,使得模型参数达到机器无穷大。
- BN-x30:与BN-x5一样,但具有初始学习速率0.045 ( 是最初的 30 倍 )。
- BN-x5-Sigmoid:与BN-x5一样,但是把激活函数ReLU换成了Sigmoid函数。我们还尝试用Sigmoid对原始的Inception进行训练,但模型仍然保持与原始相当的精度。
注:Inception 见:《Going deeper with convolutions》论文精度,并解析GoogLeNet 网络模型结构
图 4 中,我们展示了网络的验证精度和训练步数的关系。经过![]() 个训练步骤,起始准确率达到 72.2% 。
个训练步骤,起始准确率达到 72.2% 。
图4 验证集精度-训练步数
图 5 显示了每个网络达到相同 72.2% 精度所需的训练步数,以及网络达到的最大验证精度和达到该精度所需的步数。
图5 各个网络的性能比较
粗略地总结:在一定的范围内,初始学习速率越大,模型的精确度越高!并且收敛的越快!
七、GoogleNet_v1 和 GoogleNet_v2(BN) 模型结构的比较
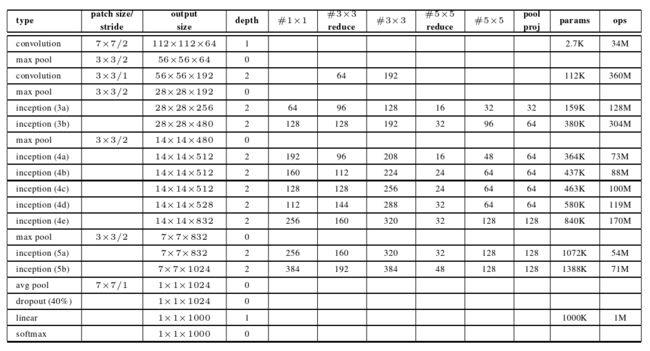
图 6 记录了相对于架构在 GoogleNet 架构上执行的更改。与 GoogLeNet 模型相比,显著的体系结构变化包括:
- 将5 × 5卷积层替换为两个连续的3 × 3卷积层。这使得网络的最大深度增加了9个权重层。同样使参数个数增加了25 %,计算量增加了30 %左右。
- 数字28×28的起始模块由2个增加到3个。
- 在模块内部,有时采用平均,有时采用最大池化。这在表的池化层对应的条目中表示。
- 任意两个Inception模块之间不存在跨板的池化层,但在模块3c,4e中的滤波器级联前采用step-2卷积/池化层。
我们的模型在第一个卷积层上使用了可分离卷积和深度乘子8。这样在提高训练时间内内存消耗的同时降低了计算开销。
图6 GoogleNet_v2(BN)
图7 GoogleNet_v1
利用零零散散的时间,陆陆续续写了三四天,希望对你有所帮助。
>>>如有疑问,欢迎评论区一起探讨!