【机器学习-西瓜书】第6章 支持向量机
一种二分类模型,是定义在特征空间上的 间隔最大的线性分类器;
SVM 的学习策略是 间隔最大化,学习算法是求解凸二次规划的最优化算法,可等价于 正则化的 合页损失函数最小化问题。
由简至繁的模型有: 线性可分支持向量机( (数据线性可分,硬间隔最大化)、线性支持向量机 (数据近似线性可分,软间隔最大化)、非线性支持向量机 (数据线性不可分,核技巧)。
当输入空间为 欧氏空间或离散集合、特征空间为希尔伯特空间时,通过核函数将 输入从输入
目录
6.1 间隔与支持向量
《统计机器学习-李航》第7.1.2节 函数间隔和几何间隔
《统计机器学习-李航》第7.1.3节 间隔最大化
1 最大间隔分离超平面
2 最大间隔分离超平面的存在唯一性
3 支持向量 和 间隔边界
6.2 对偶问题
引自《统计机器学习》:对偶最优化问题
《统计机器学习-李航》第7.1.4节 学习的对偶算法
6.3 核函数
什么样的函数可以作核函数呢?<-> positive definite kernel function
常用核函数:
《统计学习方法》7.3 非线性SVM 与 核函数
7.3.1 核技巧
核函数定义
7.3.2 正定核
函数K(x, z)满足什么条件 才能成为 核函数?
7.3.3 常用核函数
多项式核函数 (polynomial kernel function)
高斯核函数 (Gaussian kernel function)
字符串核函数 (string kernel function)
6.4 软间隔 与 正则化
若将0/1损失函数换成其他损失函数,得到更一般的学习模型:
软间隔SVM
《统计学习方法》7.2 线性SVM 与 软间隔最大化
7.2.1 线性支持向量机
7.2.2 学习的对偶算法
算法 7.3 (线性支持向量机学习算法)
7.2.3 支持向量
7.2.4 合页损失函数
6.5 支持向量回归
SVR 问题的优化目标
6.6 核方法
如何得到“核线性判别分析*(Kernelized Linear Discriminant Analysis)
《统计机器学习》7.3.4 非线性SVCM
《统计机器学习》7.4 SMO (Sequential Minimal Optimization)算法
6.1 间隔与支持向量
二分类问题:
给定训练样本集![]()
找到一个划分超平面,将不同类别的样本分开,且 该划分超平面对训练样本局部扰动的容忍性最好。划分超平面在样本空间中由w 和 b 确定,且法向量w指向的一侧为正类,另一侧为负类,可通过下式描述
![]()
样本空间中任意点x 到超平面(w, b)的距离可写为:
而对于样本点![]() ,若
,若
定义使得上述不等式()6.3) 的等号成立的样本点,被称为支持向量(support vector),两个异类支持向量到超平面的距离之和称为间隔(margin),定义如下:
欲找到具有“最大间隔 ”(maximum margin) 的划分超平面,即等价于 找到能满足式(6.3)的约束的 w 和 b,使得 γ 最大,即:
上式可等价转化为最小化下式,即支持向量机 (Support Vector Machine) 的基本型,即原始问题。
《统计机器学习-李航》第7.1.2节 函数间隔和几何间隔
一个点距离分离超平面的远近 可以表示分类预测的确信程度。上图中点A的确信程度高于点C。
在超平面wx+b=0 确定的情况下,|wx+b| 可以相对地表示 点x距离超平面的远近。
使用 y(wx+b)来表示 分类的正确性及确信度,这就是函数间隔(functional margin)。
定义7.2 (函数间隔)
对于给定的训练数据集D 和 超平面(w, b),定义超平面 (w, b)关于样本点 (xi, yi)的函数间隔为:
定义超平面(w, b)关于训练集 D 的函数间隔为 超平面 (w, b)关于 D 中所有样本点 (xi, yi)的函数间隔的最小值,即
但是选择分离超平面时,需要考虑到 等比例改变w和b后将得到不同的函数间隔,但实际上超平面并没有改变。因此 可以对分离超平面的法向量w加上某些约束,如规范化||w||=1,使得间隔确定,此时函数间隔便成为了几何间隔(geometric margin)。
定义7.3 (几何间隔)
对于给定的训练集 D 和 超平面 (w, b),定义超平面 (w, b) 关于样本点 (xi, yi)的几何间隔为:
定义超平面(w, b)关于训练集 D 的几何间隔为 超平面 (w, b)关于 D 中所有样本点 (xi, yi)的几何间隔的最小值,即
函数间隔 和 几何间隔的关系为:
《统计机器学习-李航》第7.1.3节 间隔最大化
间隔最大化的直观解释:对训练集找到几何间隔最大的超平面意味着 以充分大的确信度对训练数据进行分类,即对那些最难分的实例点 (距离超平面最近的点)也有足够大的确信度将它们分开。
1 最大间隔分离超平面
如何求得一个 几何间隔最大的分离超平面,可表示为以下 约束最优化问题:
如上一节中解释的那样,由于函数间隔的的等比例改变 对最优化问题的不等式约束没有影响,所以 取
= 1,带入式 (7.11),得到最大化
,该式等价于下式,是原始最优化问题:
算法 7.1 (线性可分支持向量机学习算法——最大间隔法)
输出:最大间隔分离超平面 和 分类决策函数
1)构建并求解约束最优化问题:
求得最优解
2)得到分离超平面 和 分类决策函数:
2 最大间隔分离超平面的存在唯一性
定理7.1 (最大间隔分离超平面的存在唯一性)
若训练集 D 线性可分,则 可将训练集 D 中的样本点完全正确分开的 最大间隔分离超平面存爱且唯一。
证明参见《统计机器学习》p101
3 支持向量 和 间隔边界
支持向量 是使约束条件式 (7.14)等号成立的点,即
6.2 对偶问题
式(6.6)是一个凸二次规划问题 (convex quadratic programming)
凸优化问题指的是 如下约束最优化问题:
目标函数
和 约束函数
均是
上的连续可微的凸函数,约束函数
为
上的仿射函数
使用拉格朗日乘子法,得到其“对偶问题” (dual problem),通过求解对偶问题 得到原始问题 (primal problem)的最优解。
具体来说,对式 (6.6)的每条约束添加拉格朗日乘子 (lagrange multiplier) αi ≥ 0,则可构建该问题的拉格朗日函数如下:
根据拉格朗日对偶性,原始问题的对偶问题 是极大极小问题:
![]()
因此,先求解 L(w, b, α)对w,b的极小,再求对α的极大。
1) 求 ![]() 。
。
令 L(w, b ,α )对 w 和 b的偏导为零,可得:
将式(6.9)带入式(6.8),并考虑式(6.10)的约束,可得到式(6.6)的对偶问题:
2)最小化上式 L(w, b, α),即求 ![]() 对 α的极大,等价于 求解对偶问题:
对 α的极大,等价于 求解对偶问题:
求解式(6.11),使用SMO (Sequential Minimal Optimization)算法:
引自《统计机器学习》:对偶最优化问题
将 式(6.11)由求极大 转换为求极小,则等价于求以下最优化问题 (对偶最优化):
解出α后,取出 w和b,可得到模型:
由于原始问题中存在 不等式约束,即![]() ,因此上述过程需要满足 KKT (Karush- Kuhn-Tucker)条件,即要求
,因此上述过程需要满足 KKT (Karush- Kuhn-Tucker)条件,即要求
![]()
《统计机器学习-李航》第7.1.4节 学习的对偶算法
定理 7.1
设
是 对偶最优化问题(7.22)~(7.24)的解,则存在下标j,使得
,并可以通过下式求得原始最优化问题的解
:
证明如下:
根据定理C.3 ,即
对于原始问题和对偶问题,假设函数
是凸函数,
是 仿射函数,且不等式约束
是严格可行的,则
分别是 原始问题和对偶问题的解 的充分必要条件是
满足如下 KKT 条件:

KKT 条件成立,可得到:
由此得到
且至少有一个
,对此 j 有:
将式(7.25)带入式(7.28)得到:
由此,分类决策函数可写成:
算法7.2 (线性可分支持向量机学习算法)
输出:分离超平面 和 分类决策函数
1)构造并求解约束最优化问题
求得最优解
2)计算
选择
的一个正分量
,计算
3)求得分离超平面 和 分类决策函数:
定义7.4 (支持向量)
考虑原始最优化问题 及对偶最优化问题,将训练集 D 中对应于
的样本点 (
)的实例
称为支持向量。
KKT条件
,对应于
的实例
,有
即
一定在 间隔边界上。
6.3 核函数
当原始空间内 不存在一个能正确划分两类样本的超平面,但原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间 使得样本可分。
令![]() 表示 x 映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为
表示 x 映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为
![]()
此时,由支持向量所确定的 最大间隔支持向量机可表示为:
其对偶问题为:
直接计算 ![]() 是很困难的,因此,设计了这样一个函数:
是很困难的,因此,设计了这样一个函数:
![]()
输入空间的内积 ![]() 变换为 在特征空间的内积
变换为 在特征空间的内积![]() ,通过它们在原始样本空间中通过 核函数k(·, ·) 计算得到。于是可重写上述对偶问题如下:
,通过它们在原始样本空间中通过 核函数k(·, ·) 计算得到。于是可重写上述对偶问题如下:
现实任务中,我们通常不知道![]() 的具体形式,那么
的具体形式,那么
什么样的函数可以作核函数呢?<-> positive definite kernel function
定理 6.1(核函数)
令 X 为输入空间,k(· , ·)是定义在 X × X 上的对称函数,则 k 是核函数 当且仅当 对于任意数据
, "核矩阵 (kernel matrix)" K 总是半正定的:
任何一个核函数都隐式地定义了一个 称为“再生核希尔伯特空间” (Reproducing Kernel Hilbert Space) 的特征空间。
常用核函数:
《统计学习方法》7.3 非线性SVM 与 核函数
7.3.1 核技巧
非线性可分问题:
给定数据集 ![]() ,如果 可使用
,如果 可使用 ![]() 中的一个超曲面将正负例正确分开,则称该问题为 非线性可分问题。
中的一个超曲面将正负例正确分开,则称该问题为 非线性可分问题。
 分为2步:
分为2步:
1. 使用一个变换 将原空间的数据映射到新空间;
2. 在新空间中 使用线性分类学习方法从训练集中学习分类模型
SVM中核技巧的基本思想是:通过一个非线性变换 将输入空间 (欧式空间或离散集合)对应于一个特征空间 (希尔伯特空间),使得在输入空间中的超曲面 对应于 特征空间的超平面。
学习是 隐式地在特征空间 进行的,不需要显示地定义特征空间 H 和 映射函数 φ,。
核函数定义
定义 7.6 (核函数)
设 ![]() 是输入空间(欧氏空间或离散集合),设 H 为特征空间(希尔伯特空间),若存在一个从
是输入空间(欧氏空间或离散集合),设 H 为特征空间(希尔伯特空间),若存在一个从 ![]() 到 H 的映射:
到 H 的映射:
![]()
使得对所有的 ![]() ,函数
,函数 ![]() 满足条件:
满足条件:
![]() ,
,
则称 ![]() 为核函数,
为核函数,![]() 是映射函数,
是映射函数,![]() 表示
表示 ![]() 和
和 ![]() 的内积。
的内积。
7.3.2 正定核
函数K(x, z)满足什么条件 才能成为 核函数?
依据函数K(x, z), 构成一个希尔伯特空间:
1. 定义映射,构成向量空间 (或线性空间)S
定义映射 Φ:
![]()
定义线性组合:
2. 在 S 上定义内积,使其成为内积空间:
对于任意的 ![]() ,且
,且
则
3. 将内积空间 完备化为 希尔伯特空间:
由 式(7.81)定义的内积可以得到范数:
![]()
此时 内积空间成为 一个赋范向量空间,一定可以使之完备化,得到Hilbert Space。
7.3.3 常用核函数
多项式核函数 (polynomial kernel function)
![]()
此时的分类决策函数为:
高斯核函数 (Gaussian kernel function)
此时的分类决策函数为:
字符串核函数 (string kernel function)
映射 ![]() 将字符串 s 对应于空间
将字符串 s 对应于空间 ![]() 的一个向量,其在 u 维上的取值为:
的一个向量,其在 u 维上的取值为:
l(i) 表示 字符串i的长度,求和在 s 中所有与 u 相同的子串上进行。
两个字符串 s 和 t 上的字符串核函数 是基于映射 ![]() 的特征空间中的内积:
的特征空间中的内积:
字符串核函数 ![]() 给出了字符串 s 和 t 中长度为n 的所有子串组成的特征向量的 余弦相似度 (cosine similarity)。
给出了字符串 s 和 t 中长度为n 的所有子串组成的特征向量的 余弦相似度 (cosine similarity)。
字符串核函数可由动态规划快速算出。
6.4 软间隔 与 正则化
允许SVM 在一些样本上出错,以缓解过拟合,为此引入“软间隔 (soft margin)”的概念。允许出错的意思是 允许某些样本不满足约束:
![]()
在最大化间隔的同时,不满足约束的样本应该尽量少。于是优化目标可写为:
但是![]() 损失函数 非凸、非连续,数学性质不好,使得式(6.29)不易直接求解。于是通常使用其他一些函数来代替,常用的有以下三种:
损失函数 非凸、非连续,数学性质不好,使得式(6.29)不易直接求解。于是通常使用其他一些函数来代替,常用的有以下三种:
hinge损失:
指数损失(exponential loss):
对率损失(logistic loss):
若将0/1损失函数换成其他损失函数,得到更一般的学习模型:
从SVM来看,上式优化目标的第一项 用于描述划分超平面的“间隔”大小;第二项 用来表述训练集上的误差。
上式中 ![]() 称为 结构风险 (structural risk),用于描述模型 f 的某些性质;第二项称为 经验风险 (empirical risk),用于描述模型与训练集的拟合程度。
称为 结构风险 (structural risk),用于描述模型 f 的某些性质;第二项称为 经验风险 (empirical risk),用于描述模型与训练集的拟合程度。
从 经验风险最小化的角度来看,![]() 可看作 正则化项,它表述了 希望模型具有何种性质(例如希望模型复杂度小),为引入领域知识 和 用户意图提供了途径,此外,还有助于削减假设空间,降低最小化训练误差的过拟风险。
可看作 正则化项,它表述了 希望模型具有何种性质(例如希望模型复杂度小),为引入领域知识 和 用户意图提供了途径,此外,还有助于削减假设空间,降低最小化训练误差的过拟风险。
软间隔SVM
引入“松弛变量”(slack variables)ξi ≥ 0,则优化目标为:
由上式可看出:每个样本 都有一个对应的slack variable,用来表示 该样本不满足约束(6.28)的程度。
学习的对偶算法参见下方 7.2.2
《统计学习方法》7.2 线性SVM 与 软间隔最大化
7.2.1 线性支持向量机
线性不可分 意味着 某些样本点
不能满足
的约束条件。因此 对每个样本点
引进一个 松弛变量
,使得 函数间隔
加上 松弛变量
≥1,于是线性不可分的线性支持向量机的学习问题变为 如下凸二次规划问题(原始问题):
C > 0称为惩罚系数,式(3.21)包含两层含义:1)使第一项尽量小即间隔尽量大;2)使误分类点的个数尽量少,C为调和系数。
7.2.2 学习的对偶算法
写出原始最优化问题的 拉格朗日函数:
1)求
.
求
关于
的偏导,并令其为零:
得到:
带入式(7.40)得到:
2)求
对 α的极大,即对偶问题:
等价于如下对偶问题:
与硬间隔下的对偶问题相比,唯一的差别在于 对偶变量的约束不同:硬间隔是
,软间隔是
算法 7.3 (线性支持向量机学习算法)
输出:分离超平面 和 分类决策函数
1) 选择惩罚参数 C>0,构造并求解 凸二次规划问题:
求得最优解
.
选择
的一个分量
适合条件
,计算
3)求得分离超平面 和 分类决策函数:
7.2.3 支持向量
7.2.4 合页损失函数
先行支持向量机的另一种解释,可理解为 最小化以下目标函数:
函数
称为“合页损失函数(hinge loss function)”,下标“+”表示 以下取正值的函数:
即当样本点 (xi, yi)被正确分类且函数间隔
大于1 时,损失为0,否则损失为
,
6.5 支持向量回归
- 传统回归模型
直接基于 模型输出f(x) 与 真是输出y 之间的差别来计算损失。
- 支持向量回归 (Support Vector Regression)
假设可以容忍 f(x) 与 y 之间最多有 ε 的偏差,即当且仅当 |f(x) - y| ≥ ε 时,才计算损失。
SVR 问题的优化目标
引入松弛变量 ![]() ,优化目标可写为:
,优化目标可写为:
引入lagrange multiplier (4个,均≥0),得到lagrange function:
令 ![]() 关于
关于 ![]() 的偏导为零,可得:
的偏导为零,可得:
上述结果代回式(6.46),可得到SVR的对偶问题:
6.6 核方法
定理 6.2 (表示定理)
令 H 为核函数 k 对应的再生核 希尔伯特空间,![]() 表示 H 空间中关于 h 的范数,对于任意单调递增函数
表示 H 空间中关于 h 的范数,对于任意单调递增函数 ![]() 和 任意非负损失函数
和 任意非负损失函数 ![]() , 优化问题:
, 优化问题:
![]()
其解总可以写为:
如何得到“核线性判别分析*(Kernelized Linear Discriminant Analysis)
假设通过某种映射 ![]() 将样本映射到特征空间 F中,然后再 F 中执行线性判别分析,以求得:
将样本映射到特征空间 F中,然后再 F 中执行线性判别分析,以求得:
![]()
此时,KLDA 的学习目标为:
令 ![]() 表示第
表示第 ![]() 类样本的集合,其样本数为
类样本的集合,其样本数为 ![]() ,第 i 类样本在特征空间 F 中的均值为:
,第 i 类样本在特征空间 F 中的均值为:
![]()
《统计机器学习》7.3.4 非线性SVCM
将线性SVM对偶形式中的 内积换成核函数,便可将线性SVM扩展到非线性SVM。
算法 7.4 (非线性SVM学习算法)
《统计机器学习》7.4 SMO (Sequential Minimal Optimization)算法
待续。。。。


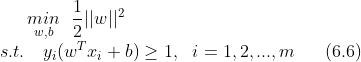
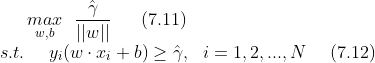







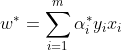




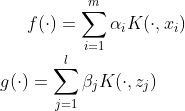

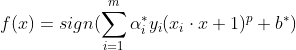
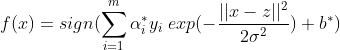

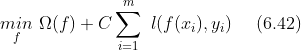




![\sum_{i=1}^{m}[1-y_{i}(w\cdot x_{i} +b)]_{+} + \lambda ||w||^{2} \ \ \ (7.57)](http://img.e-com-net.com/image/info8/b6475ae904684fd48616ebdd60a95d4f.gif)



