深度学习笔记 —— 权重衰退 + 丢弃法
硬性限制
柔性限制
 “罚”(即后一项)的引入,使得最优解往原点走,使得w的绝对值会小一些,从而降低了整个模型的复杂度
“罚”(即后一项)的引入,使得最优解往原点走,使得w的绝对值会小一些,从而降低了整个模型的复杂度
为什么要用权重衰退呢?
因为数据中有噪音存在,往往使得w比较大,从而使模型得到的解与最优解相比,w会比较大。当我们采用权重衰退的方法以后,会把w拉小,因此更容易将解拉到最优解附近。
此处噪音不是指固定噪音,而是随机噪音。
加入了噪音,但并不希望期望有所改变
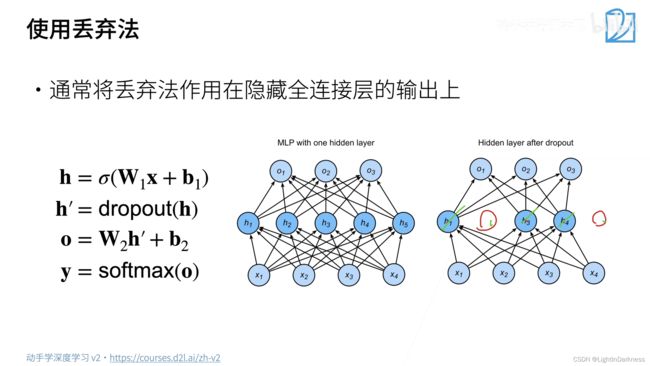
dropout是一个正则项,正则项只在训练中使用,因为它只会对权重产生影响,预测的时候参数并不需要发生变化
很少用在CNN之类的模型上(原因之后会解释)。p常取0.1,0.5,0.9等
import torch
from torch import nn
from d2l import torch as d2l
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
if dropout == 1:
return torch.zeros_like(X)
if dropout == 0:
return X
mask = (torch.rand(X.shape) > dropout).float() # 生成0到1之间的均匀随机分布
return mask * X / (1.0 - dropout)
X = torch.arange(16, dtype=torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1))
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
dropout1, dropout2 = 0.2, 0.5
class Net(nn.Module):
def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2, is_training=True):
super(Net, self).__init__()
self.num_inputs = num_inputs
self.training = is_training
self.lin1 = nn.Linear(num_inputs, num_hiddens1)
self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
self.lin3 = nn.Linear(num_hiddens2, num_outputs)
self.relu = nn.ReLU()
def forward(self, X):
H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs)))) # 第一个隐藏层的输出
if self.training == True:
H1 = dropout_layer(H1, dropout1)
H2 = self.relu(self.lin2(H1))
if self.training == True:
H2 = dropout_layer(H2, dropout2)
out = self.lin3(H2)
return out
net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)
num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
'''
# concise version
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
dropout1, dropout2 = 0.2, 0.5
num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# concise version
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Dropout(dropout1),
nn.Linear(256, 256), nn.ReLU(), nn.Dropout(dropout2), nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
'''