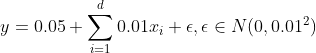动手学深度学习笔记（一）——权重衰退

        一直在csdn上学习别人发的博客，第一次尝试自己写博客，今天周日，在实验室小学一会，发现自己有些不明白的点突然想明白了，想记录一下在学习过程中遇到的难点或者有些迷惑的地方，希望自己以后能掌握牢固，并把自己的一些看法分享给大家，欢迎一起讨论。

目录

一、引言

二、权重衰退的作用和原因

1、为什么权重矩阵稀疏可以防止过拟合?

2、为何权重参数 w减小就可以防止过拟合?

        其他缓解过拟合的方法：

          三、权重衰退的实现

通过限制参数的范围来控制模型容量

          四、L1范数和L2范数的应用区别

 五、代码实现权重衰减(pytorch)

---

一、引言

权重衰减weight decay

其行为即直接导致每轮迭代过程中的权重weight参数被削减/惩罚了一部分，这样的话我们在训练的反向传播过程中，得到的权重w就会尽可能小，从而一定程度上减小了模型的复杂度，从而一定程度上解决了过拟合问题。

二、权重衰退的作用和原因

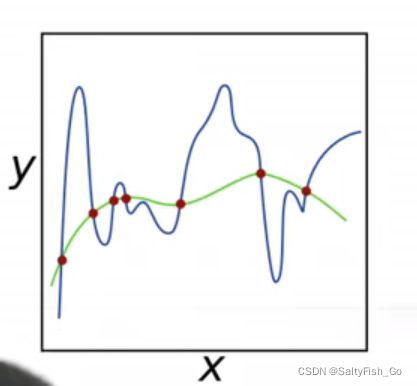
过拟合是因为模型复杂度太高，对特征简单的数据直接进行重复，拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大，不能总结出主要的影响因素（权重高的特征），而导致对验证数据不能有较好的预测效果。而权重衰退就是通过正则化技术来缓解一些过拟合产生的影响。

看懂了权重衰减的作用机理，但是一直不明白为什么能减缓过拟合的程度，后来学到了更直观的解释就明白了：

1、为什么权重矩阵稀疏可以防止过拟合?

可以从两个方面来理解:

1）特征选择(Feature Selection)：稀疏性可以实现特征的自动选择, 可以在进行预测时减少无用信息的干扰

大家对稀疏规则化趋之若鹜的一个关键原因在于它能实现特征的自动选择。一般来说，xi 的大部分元素（也就是特征）都是和最终的输出 yi 没有关系或者不提供任何信息的，在最小化目标函数的时候考虑 xi 这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的信息反而会被考虑，从而干扰了对正确 yi 的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命，它会学习地去掉这些没有信息的特征，也就是把这些特征对应的权重置为 0。

2）可解释性(Interpretability)：较稀疏的模型表示最终的预测结果只与个别关键特征有关, 这符合实际生活中的历史经验

另一个青睐于稀疏的理由是，模型更容易解释。例如患某种病的概率是y，然后我们收集到的数据x是1000维的，也就是我们需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设我们这个是个回归模型： y=w1×x1+w2×x2+…+w1000×x1000+by=w1×x1+w2×x2+…+w1000×x1000+b （当然了，为了让 y 限定在 [0,1][0,1] 的范围，一般还得加个Logistic函数）。通过学习，如果最后学习到的 w就只有很少的非零元素，例如只有 5 个非零的 wi ，那么我们就有理由相信，这些对应的特征在患病分析上面提供的信息是巨大的，决策性的。也就是说，患不患这种病只和这5个因素有关，那医生就好分析多了。但如果 1000 个 wi 都非 0，医生面对这 1000 种因素，累觉不爱.

2、为何权重参数 w减小就可以防止过拟合?

直观解释:

更小的权值w，从某种意义上说，表示网络的复杂度更低，对数据的拟合刚刚好（这个法则也叫做奥卡姆剃刀），而在实际应用中，也验证了这一点，L2正则化的效果往往好于未经正则化的效果

“数学一点”的解释:

过拟合的时候，拟合函数的系数往往非常大，为什么？过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大. 而正则化是通过约束参数的范数使其不要太大，所以可以在一定程度上减少过拟合情况。

 

        其他缓解过拟合的方法：

1、减少一些不重要特征的数量，限制特征数量可以减小相对无关特征对模型的影响。比如这里，本来在20个变量的矩阵中我们只有四个有效的输入，正常来说权重矩阵应该只有四个非零值，但是在学习所有变量后（而不是单独只取前四个变量），模型学习到的权重矩阵是给后面的16个变量也分配了一定的矩阵，这在一定程度上导致了过拟合。也就是在训练集上的表现和验证集中有明显的区别。

max_degree = 20  # 多项式的最大阶数
n_train, n_test = 100, 100  # 训练和测试数据集大小
true_w = np.zeros(max_degree)  # 分配大量的空间
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])

features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
    poly_features[:, i] /= math.gamma(i + 1)  # gamma(n)=(n-1)!
# labels的维度:(n_train+n_test,)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)

 2、可以收集更多的训练数据。

三、权重衰退的实现

权重衰减（weight decay）是最广泛使用的正则化的技术之一， 它通常也被称为L2正则化。 这项技术通过函数与零的距离来衡量函数的复杂度， 因为在所有函数ff中，函数f=0（所有输入都得到值0） 在某种意义上是最简单的。但是我们应该如何精确地测量一个函数和零之间的距离呢？

一种简单的方法是通过线性函数 f(x)=w⊤xf(x)=w⊤x 中的权重向量的某个范数来度量其复杂性， 例如 。 要保证权重向量比较小， 最常用方法是将其范数作为惩罚项加到最小化损失的问题中。 将原来的训练目标最小化训练标签上的预测损失， 调整为最小化预测损失和惩罚项之和。 现在，如果我们的权重向量增长的太大， 我们的学习算法可能会更集中于最小化权重范数

通过限制参数的范围来控制模型容量

1、使用L2范数作为硬性限制

        ·不用限制偏移b的大小，无影响

        ·如果比较小，那么会有更强的正则项

2、使用L2范数进行柔性限制

使用lamda作为超参数，越大就权重限制越大

通过计算梯度对参数进行更新：

可以看出来加上正则项的loss function的梯度只是在w t  ​这里加上了一个项，通常− η λ <1那么我们得到的梯度更新量就会在梯度更新的方向上回退一些，从而控制了梯度更新的步子.

---

四、L1范数和L2范数的应用区别

为什么我们首先使用L2范数，而不是L1范数。 事实上，这个选择在整个统计领域中都是有效的和受欢迎的。 L2正则化线性模型构成经典的岭回归（ridge regression）算法， L1正则化线性回归是统计学中类似的基本模型， 通常被称为套索回归（lasso regression）。 使用L2范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。 这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。 在实践中，这可能使它们对单个变量中的观测误差更为稳定。 相比之下，L1惩罚会导致模型将权重集中在一小部分特征上， 而将其他权重清除为零。 这称为特征选择（feature selection），这可能是其他场景下需要的。

L1 的优点: 能够获得更加稀疏的模型.
L1 的缺点: 加入 L1 后会使得目标函数在原点不可导, 需要做特殊处理

L2 的有点: 在任意位置都可导, 优化求解过程比较方便, 而且更加稳定
L2 的缺点: 无法获得真正的稀疏模型

在实际应用过程中, 大部分情况下都是 L2 正则的效果更好, 因此推荐优先使用 L2 正则

两者的区别

1. L1 相对于 L2 能够产生更加稀疏的模型
2. L2 相比于 L1 对于离异值更敏感(因为平方的原因, L2 对于大数的乘法比对小数的惩罚大)
3. L1 和 L2 梯度下降速度不同: 前者梯度恒定, 并且接接近于 0 的时候会很快将参数更新成0, 后者在接近于0 时, 权重的更新速度放缓, 使得不那么容易更新为0 (这也解释了为什么 L1 具有稀疏性)
4. 二者解空间性状不同

五、代码实现权重衰减(pytorch)

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

生成一些数据，生成公式如下： 

我们选择标签是关于输入的线性函数。 标签同时被均值为0，标准差为0.01高斯噪声破坏。 为了使过拟合的效果更加明显，我们可以将问题的维数增加到d=200d=200， 并使用一个只包含20个样本的小训练集。

n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5 true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05 train_data = d2l.synthetic_data(true_w, true_b, n_train) train_iter = d2l.load_array(train_data, batch_size) test_data = d2l.synthetic_data(true_w, true_b, n_test) test_iter = d2l.load_array(test_data, batch_size, is_train=False)

下面开始从0实现权重衰减 

#初始化模型参数
def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]

 #定义L2范数惩罚

def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2

下面的代码将模型拟合训练数据集，并在测试数据集上进行评估。 从 3节以来，线性网络和平方损失没有变化， 所以我们通过d2l.linreg和d2l.squared_loss导入它们。 唯一的变化是损失现在包括了惩罚项。

def train(lambd):
    w, b = init_params()
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
    num_epochs, lr = 100, 0.003
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
#作图函数
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L2范数惩罚项，
            # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(X), y) + lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        if (epoch + 1) % 5 == 0:#更新图
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
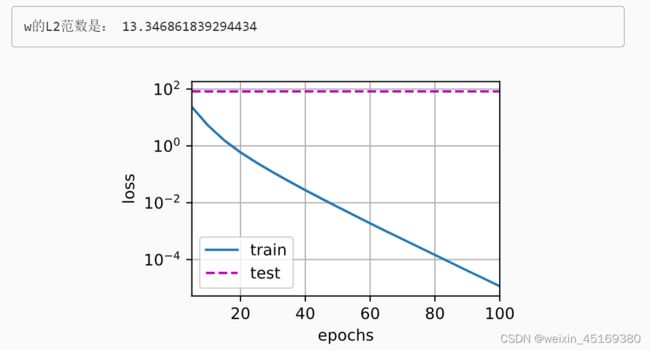
    print('w的L2范数是：', torch.norm(w).item())

下面对有无正则化（是否权重衰减）进行对比， 

train(lambd=0)

我们现在用lambd = 0禁用权重衰减后运行这个代码。 注意，这里训练误差有了减少，但测试误差没有减少， 这意味着出现了严重的过拟合

 train(lambd=3)

下面，我们使用权重衰减来运行代码。 注意，在这里训练误差增大，但测试误差减小。 这正是我们期望从正则化中得到的效果。