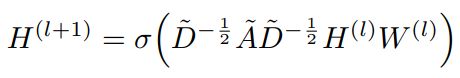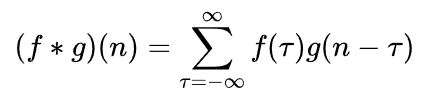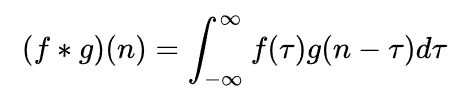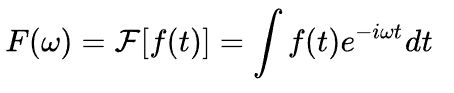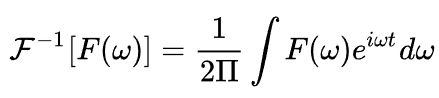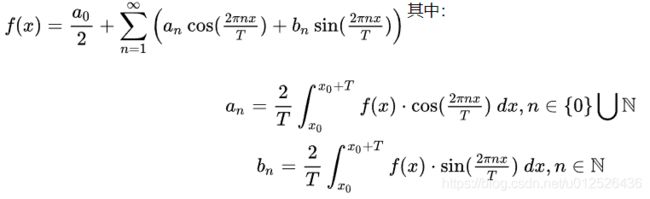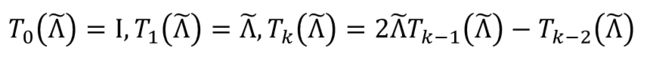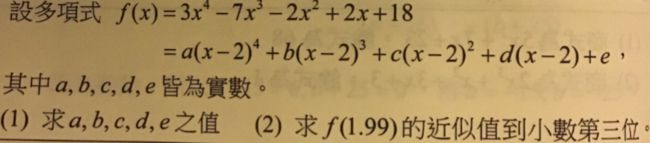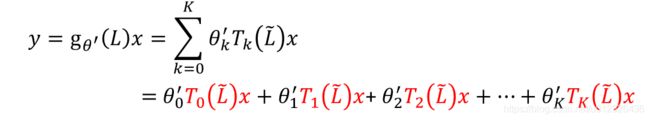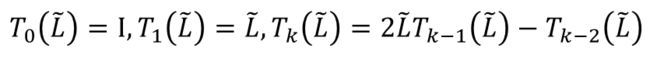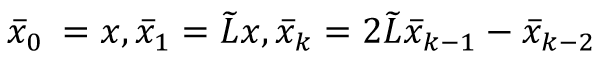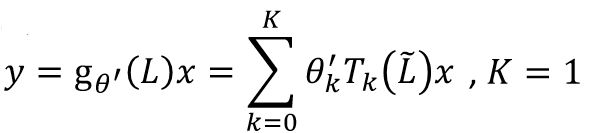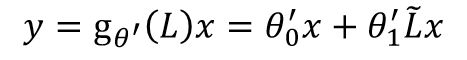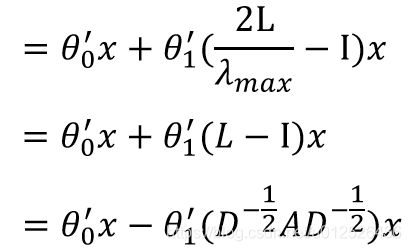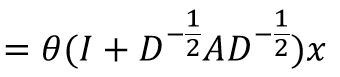图卷积神经网络GCN降维全解析
1.前言
本文是笔者对GCN的一个知识整理与汇总,会尽可能从通俗易懂的角度来为0基础的同学解释GCN的推导过程,GCN的推导总体来说较为复杂,笔者的理解可能会有偏差,如有解释错误的地方,欢迎指正交流。
图卷积神经网络公式很简单,如下所示,即邻接矩阵和度矩阵与节点信号(特征)的非线性变换。
公式虽简单,但背后包含很多复杂数学原理。GCN有两种推导方式,第一种是基于傅里叶变换的形式,该方法涉及到很多预备知识,大量的数学推导;第二种是基于message passing的方式,该方式便于理解。本文会尽可能从通俗易懂的角度来把两种方式解释清楚。
2.基于傅里叶变换的图卷积
如果你不想去深入了解严格的数学推导过程,建议直接跳过本节,直接看第三节基于message passing的GCN原理说明,包括目前两个比较常用的包pytorch_geometric与dgl都是采用的message passing原理。
在开始讲解前,我们先介绍一些预备知识
2.1 卷积
在数学上,卷积分为离散卷积和连续卷积,我们称 ( f ∗ g ) ( n ) (f*g)(n) (f∗g)(n)为 f , g f,g f,g的卷积
只看公式很难理解其含义,我们看两个具体的例子。
2.1.1 离散卷积的例子
假如我们抛了两个骰子,我们想知道两个骰子相加的点数为4的概率。我们设 f ( i ) f(i) f(i)表示第一个骰子抛出 i i i的概率,设 g ( i ) g(i) g(i)表示第二个骰子抛出 i i i的概率,那么抛出点数和为4个情况有 f ( 1 ) g ( 3 ) f(1)g(3) f(1)g(3), f ( 2 ) g ( 2 ) f(2)g(2) f(2)g(2), f ( 3 ) g ( 1 ) f(3)g(1) f(3)g(1),加起来的概率为
P = f ( 1 ) g ( 3 ) + f ( 2 ) g ( 2 ) + f ( 3 ) g ( 1 ) P = f(1)g(3)+f(2)g(2)+f(3)g(1) P=f(1)g(3)+f(2)g(2)+f(3)g(1)
转换成标准化的形式为
( f ∗ g ) ( 4 ) = ∑ τ = 1 3 f ( τ ) g ( 4 − τ ) (f*g)(4)=\sum_{ \tau=1}^3f(\tau)g(4-\tau) (f∗g)(4)=τ=1∑3f(τ)g(4−τ)
2.1.2 连续卷积的例子
某馒头铺生意很好,供不应求,于是使用了一台机器来做馒头,假设生产馒头的速度是 f ( τ ) f (\tau) f(τ),那么一天生产的馒头就是
∫ 0 24 f ( τ ) d τ \int_0^{24}f(\tau)d\tau ∫024f(τ)dτ
馒头生产好如果不及时销售的话就会慢慢腐坏,设腐坏的函数为 g ( τ ) g(\tau) g(τ)
第一个小时生产出来的馒头,一天后会经历24小时的腐坏,第二个小时生产出来的馒头,一天后会经历23小时的腐坏,一天后,馒头总共腐坏了
∫ 0 24 f ( τ ) g ( 24 − τ ) d τ \int_0^{24}f(\tau)g(24-\tau)d\tau ∫024f(τ)g(24−τ)dτ
2.1.3 CNN中的卷积
在CNN中的卷积实际上属于离散卷积,从上文我们也可以发现,离散卷积实际上就是一个加权求和的过程,CNN中的卷积本质上就是利用一个共享参数的卷积核,通过计算中心像素点以及相邻像素点的加权和来构成feature map实现空间特征的提取,当然加权系数就是卷积核的权重系数。
2.2 傅里叶变换
这里又引入了一个新的概念,傅里叶变换,这一节我不会把傅里叶变换讲的太详细,理解GCN我个人觉得对傅里叶有一个大致的理解就ok了,我们先看个小例子。
假如你想调制一杯正宗的mojito,但是你并不知道其中薄荷、柠檬汁、苏打水、朗姆酒的比例成分,现在你有一杯酒吧中买到的mojito,如果你能从这杯调制好的mojito中分离出其各成分,你就可以知道其比例,从此你就是mojito调制大师。 这里的成分分析就需要用到一个过滤器,不同的过滤器过滤不同的成分,过滤的过程实际上就是所谓的傅里叶变换。知道了mojito的配方后,你就可以自己购买这些基础配料来调配自己的mojito,这个调配的过程就是傅里叶逆变换。
有了这个概念后,我们来看傅里叶变换真实的应用场景。傅里叶变换主要是用于把信号从时域变换到频域,而变换的过程,需要把不同频率的信号先过滤出来,如下图所示。所以如果你想把一段录音中的杂音给去处,就可以考虑使用傅里叶变换,先把杂音与人声过滤出来,再把杂音去除,最后进行傅里叶逆变换。
傅里叶变换的目的是把信号转到不同的子信号对应的空间中(频域), 那怎么把一个信号映射到另一个空间呢,很简单,和一组基向量相乘,公式中 f ( t ) f(t) f(t)表示的是信号, e − i w t e^{-iwt} e−iwt表示的是另一个空间的一组基,所以傅里叶变换的公式表示的就是把信号映射到新的空间然后计算其积分。
傅里叶逆变换公式如下
2.3 傅里叶变换的简单推导
接下来我们对傅里叶变换公式做一个简单的推导,详细推导请点击这里,当然,这一部分不影响你对整个GCN原理的理解,可以选择跳过直接阅读2.4节的内容。
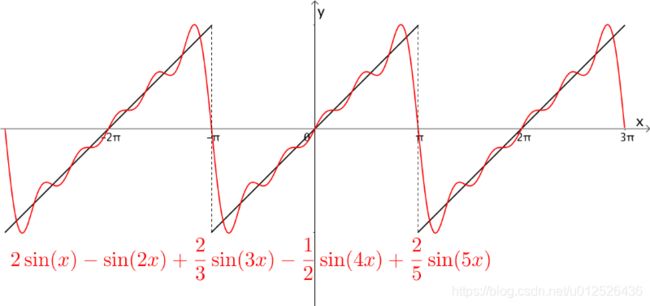
拉格朗日等数学家发现某些周期函数可以由三角函数的和来表示,比如下图中,黑色的斜线就是周期为 2 π 2\pi 2π的函数,而红色的曲线是三角函数之和,可以看出两者确实近似:
另一位数学家傅里叶则推导出任意周期函数都可以写成三角函数之和,例如某函数 f ( x ) f(x) f(x)其周期是 T T T,那么可以用三角函数近似表示为
这个就是我们常听到的傅里叶级数,所以我们只需要计算出 a n a_n an、 b n b_n bn、 C C C这三个参数就能得到最后的近似解,最终的结果如下
利用欧拉公式 e i x = c o s x + i s i n x e^{ix}=cosx+isinx eix=cosx+isinx,可以把 c o s x cosx cosx与 s i n x sinx sinx表示为
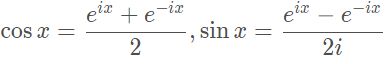
然后我们把傅里叶级数中的 c o s x cosx cosx与 s i n x sinx sinx替换为 c n c_n cn表示,则有
f ( x ) = ∑ n = − ∞ ∞ c n e i 2 π n x T f(x)=\sum_{n=-\infty}^{\infty} c_n e^{i\frac{2\pi nx}{T}} f(x)=n=−∞∑∞cneiT2πnx
其中
c n = 1 T ∫ x 0 x 0 + T f ( x ) ⋅ e − i 2 π n x T d x c_n=\frac{1}{T} \int _{x_0}^{x_0+T} f(x)·e^{-i\frac{2 \pi nx}{T}}dx cn=T1∫x0x0+Tf(x)⋅e−iT2πnxdx
改成连续性的
f ( x ) = ∫ − ∞ ∞ c n e i 2 π n x T d n f(x)=\int_{-\infty}^{\infty} c_n e^{i\frac{2\pi nx}{T}}dn f(x)=∫−∞∞cneiT2πnxdn
用 w w w表示频率, F ( w ) F(w) F(w)表示 c n c_n cn则有
f ( x ) = ∫ − ∞ ∞ F ( w ) e i w x d w f(x)=\int_{-\infty}^{\infty} F(w) e^{iwx}dw f(x)=∫−∞∞F(w)eiwxdw
这个公式就是傅里叶逆变换(因为这里是在找组成原始信号的子信号),根据上面的公式和 c n c_n cn的表达式,我们可以得到 F ( w ) F(w) F(w),这个就是傅里叶变换,注意这里的公式和上文提到的有一个 1 2 π \frac{1}{2\pi} 2π1的区别,这个和频率有关系

2.4 图上如何实现卷积
卷积操作通常是在欧几里得空间内进行计算,然而graph是一个拓扑结构,并不满足欧几里得结构。也就是说要么我们找到一种方法能让卷积操作在拓扑结构中进行计算,要么把拓扑结构的数据转变到欧几里得空间中再进行卷积,GCN的思想就是后者,先采用傅里叶变换把信号映射到频域进行卷积,之后再映射回时域空间。
这一部分的内容是GCN的核心推导部分,各位拉好稳好以免翻车,首先我们定义几个符号
- 图 G = ( V , E ) , N = ∣ V ∣ G=(V,E),N=|V| G=(V,E),N=∣V∣
- 邻接矩阵 A ∈ R N × N A \in R^{N×N} A∈RN×N
- 度矩阵 D ∈ R N × N D \in R^{N×N} D∈RN×N
- 节点的信号 f : V → R N f:V \to R^N f:V→RN 其中 f i f_i fi表示的是 i i i节点的信号,这里也可以理解为对应节点的特征
- 拉普拉斯矩阵 L = D − A L=D-A L=D−A, L L L 是一个半正定矩阵(半正定矩阵的特征值均大于等于0),我们这里考虑的是一个无向图,所以 L L L是一个对称阵,拉普拉斯矩阵特征分解后为 L = U Λ U T L=U \Lambda U^T L=UΛUT, Λ \Lambda Λ是一个对角阵, U U U是对应的特征向量组成的矩阵,这些特征向量都是正交的。
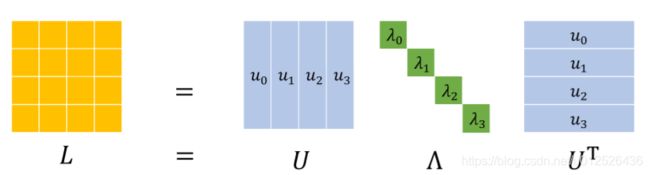
2.4.1 图上的傅里叶变换
有了上面的概念,我们需要考虑一个问题,如果想在图上使用傅里叶变换,那么我们就需要找到这样的一组基,然后把我们的节点信号(特征)映射到频域。在graph中,如果要找到一组这样的基,自然会考虑到拉普拉斯矩阵,对其做特征分解,得到其对应的特征值与特征向量, n n n维空间中 n n n个线性无关的向量可以构成空间的一组基,拉普拉斯矩阵是一个对称的半正定矩阵,其特征向量刚好是正交基,因此我们可以得到这样的一个傅里叶变换公式
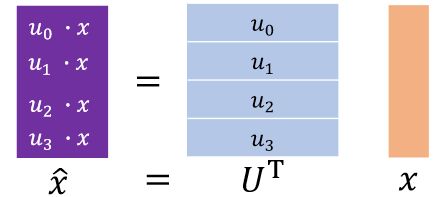
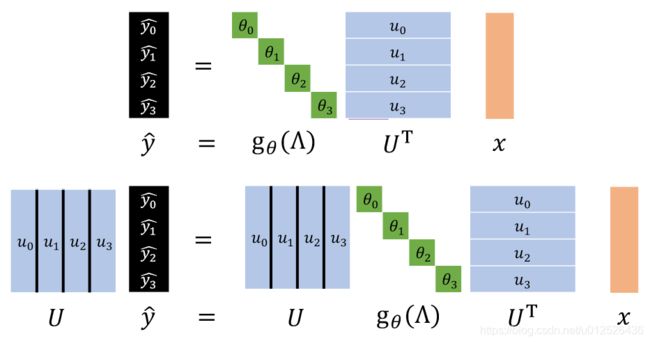
x ^ = U T x \hat x=U^T x x^=UTx
其中 U T U^T UT是拉普拉斯矩阵的特征向量组成的矩阵的转置, x x x是节点信号。
降维解释下这个公式, U T U^T UT是一个包含了多个基的矩阵,每一行的向量表示一个基,每个基可以理解为一个过滤器,我们的目的就是要用这个过滤器把 x x x过滤到自己的那个维度上。其实这里甚至可以理解为attention,不同的基对 x x x取了一个加权平均数。
有了傅里叶变换我们还需要傅里叶逆变换来把结果从频域变回时域,其计算公式如下,其中 U U U是拉普拉斯矩阵的特征向量组成的矩阵
x = U x ^ x = U \hat x x=Ux^
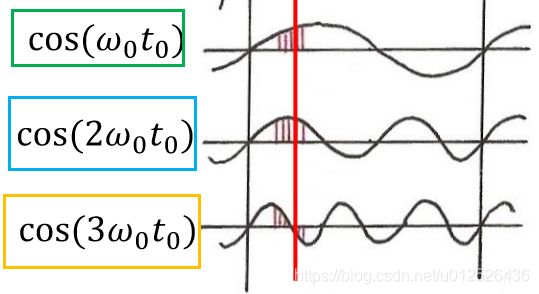
为什么直接和特征向量相乘就可以了呢?我们看个具体的例子,假如我们在时域的原函数的图如下,其中红线表示 t 0 t_0 t0时刻,我们这只考虑 t 0 t_0 t0时刻
该函数是由三个余弦函数构成
a 1 c o s ( w 0 t 0 ) + a 2 c o s ( w 0 t 0 ) + a 3 c o s ( w 0 t 0 ) a_1cos(w_0t_0)+a_2cos(w_0t_0)+a_3cos(w_0t_0) a1cos(w0t0)+a2cos(w0t0)+a3cos(w0t0)
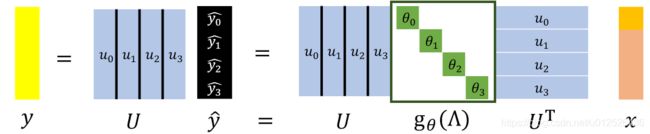
傅里叶变换是过滤出对应的 c o s ( w i t i ) cos(w_it_i) cos(witi)并计算出 a i a_i ai,傅里叶逆变换就是把 c o s ( w i t i ) cos(w_it_i) cos(witi)与 a i a_i ai乘回去,说白了就是重新构造出上面的傅里叶级数的公式。其中 a i a_i ai就是我们傅里叶变换后的结果 u i ⋅ x u_i·x ui⋅x, c o s ( w i t i ) cos(w_it_i) cos(witi)就是对应的特征向量在 i i i时刻的值。所以傅里叶逆变换就是用 x = U x ^ x = U \hat x x=Ux^,表示成图的形式如下
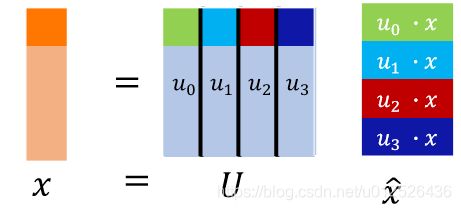
2.4.2 图上的卷积
有了以上的知识铺垫,我们就可以开始进行卷积操作了,在GCN中,我们的卷积核是特征值的一个函数,其公式如下
y ^ = g θ ( Λ ) x ^ \hat y = g_\theta(\Lambda) \hat x y^=gθ(Λ)x^
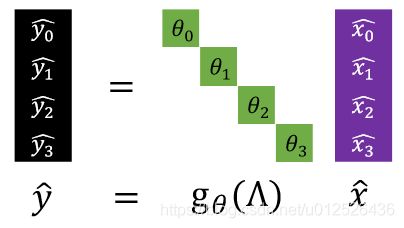
这里特征值是一个对角阵,和 x ^ \hat x x^相乘只有对应位置的值会保留下来。接下来我们把 x ^ \hat x x^展开,然后把卷积后的结果进行傅里叶逆变换
最终 y y y就是我们卷积之后的结果,其公式为
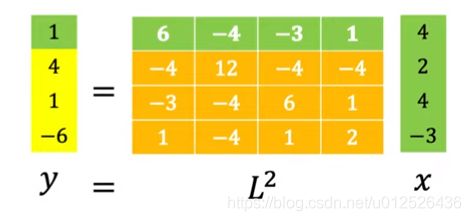
y = g θ ( U Λ U T ) x = g θ ( L ) x y=g_\theta(U\Lambda U^T)x=g_\theta(L)x y=gθ(UΛUT)x=gθ(L)x
也就是说我们的结果就是拉普拉斯矩阵一个变换后与节点信号 x x x相乘后的值,我们要学习的参数就是特征值对应的参数即 g θ ( Λ ) g_\theta(\Lambda) gθ(Λ)的参数 θ \theta θ。到这一步其实已经距离我们开篇介绍的GCN公式很接近了,其中 H 0 = X H^0=X H0=X,整理一下是这个样子的
H l + 1 = σ ( L H l W l ) = σ ( ( D − A ) H l W l ) H^{l+1}=\sigma(LH^{l}W^{l})=\sigma((D-A)H^{l}W^{l}) Hl+1=σ(LHlWl)=σ((D−A)HlWl)
2.4.3 GCN的优化
到目前为止实际上GCN已经可以用了,但是有两个很大的问题
- GCN时间复杂度和节点数是呈正比的,需要做特征分解,并且还有复杂的矩阵乘法,时间复杂度达到了 O ( N 2 ) O(N^2) O(N2),也就是说节点越多,计算量越大
- 非局部卷积,在CNN中卷积都是关注的局部特征,但是我们目前的GCN并不是局部特征
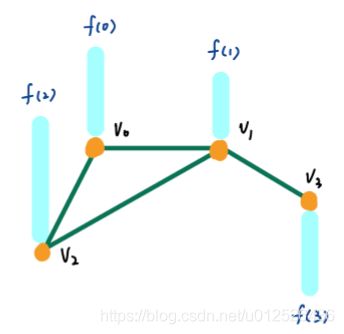
看个例子,我们有如下这样一个图
因为 g θ ( L ) g_\theta(L) gθ(L)可以是任意的函数,假设 g θ ( L ) = c o s ( L ) g_\theta(L)=cos(L) gθ(L)=cos(L),对其做泰勒展开
g θ ( L ) = I − L 2 2 ! + L 4 4 ! . . . g_\theta(L)=I-\frac{L^2}{2!}+\frac{L^4}{4!}... gθ(L)=I−2!L2+4!L4...
因为 g θ ( L ) g_\theta(L) gθ(L)可以是任意的函数,如果 g θ ( L ) g_\theta(L) gθ(L)就是 L L L,则卷积之后的结果为

因为图中0节点和3节点没有直连相连,所以 x x x与 L L L相乘,没有相连的节点的计算结果是0,这没啥问题,但是如果 g θ ( L ) g_\theta(L) gθ(L)取 L 2 L^2 L2
卷积后的结果没有相连的点的计算结果非0,这就导致了卷积之后的结果不是局部的,也就是说, L L L的指数和局部性呈反比,如果 L L L的指数 N N N,那么卷积的结果就会看到全局的一个值。为了解决这个问题,需要采用一个多项式来替代 g θ ( L ) g_\theta(L) gθ(L),而这个多项式的次数最高为 K K K, K K K表示的就是局部的大小。
g θ ( L ) = ∑ k = 1 K θ k L k g_\theta(L) = \sum_{k=1}^K \theta_kL^k gθ(L)=k=1∑KθkLk
解决了局部问题,我们还需要解决时间问题,为了降低时间复杂度,这里引入了切比雪夫多项目,切比雪夫多项式的计算方法是递归的形式, 如下图所示。
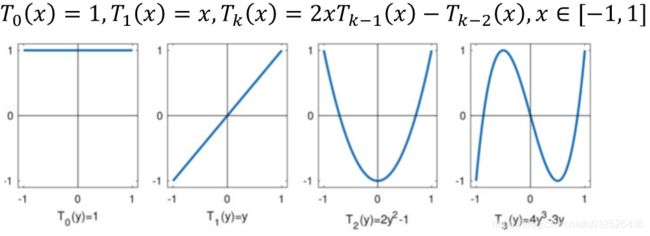
注意,切比雪夫多项式的 x x x必须属于[-1,1],所以我们要对拉普拉斯的特征值做一个变换
Λ ~ = 2 Λ λ m a x − I , λ ~ ∈ [ − 1 , 1 ] \tilde{\Lambda}=\frac{2\Lambda}{\lambda_{max}}-I,\tilde{\lambda} \in[-1,1] Λ~=λmax2Λ−I,λ~∈[−1,1]
变换后可以得到这样的切比雪夫多项式
最后我们需要学习的参数就变为了切比雪夫多项式每一项的 θ ′ \theta ' θ′
那为什么切比雪夫多项式计算就快呢,我们先看一个数学题
假如我们要求上图中的 f ( 1.99 ) f(1.99) f(1.99),实际上计算起来会很麻烦,如果我们能先求出对应的 a , b , c , d , e a,b,c,d,e a,b,c,d,e,那计算量就少了很多,切比雪夫多项式其实和这个题目是一个道理。我们本来要求 Λ k \Lambda^k Λk,但是我们对 Λ \Lambda Λ做了一个多项式的转换,只需要求其前面的参数 θ ’ \theta ’ θ’即可。这里我们把切比雪夫多项式展开看一下。
![]()
进一步简化式子,我们设 T k ( L ~ ) x = x ˉ k T_k(\tilde L)x=\bar x_k Tk(L~)x=xˉk,则有
把 x ˉ \bar x xˉ带入到卷积的式子中
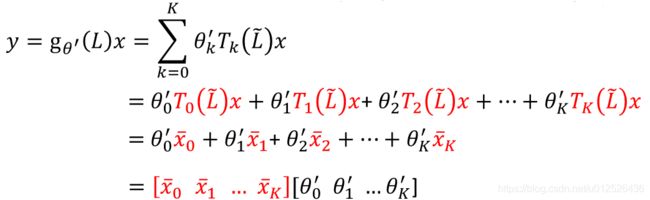
可以看到,结果就是 x x x与 θ \theta θ的点积,我们需要学习的参数是 θ ′ \theta ' θ′, x ˉ \bar x xˉ只需要采用递归的形式进行计算即可,时间复杂度为 O ( K ) O(K) O(K)
GCN最终是把 K K K设置为了1
回顾下上文 L ~ = 2 L λ m a x − 1 \tilde L=\frac{2L}{\lambda_{max}}-1 L~=λmax2L−1,GCN的 L L L通常都会先做一个归一化(不归一化可能会出现梯度消失的问题),即 L = I − D − 1 2 A D − 1 2 L=I-D^{- \frac{1}{2} }AD^{- \frac{1}{2} } L=I−D−21AD−21,归一化后 L L L的最大特征值会小于2,这里我们近似取 λ m a x = 2 \lambda_{max}=2 λmax=2
为了抑制参数数量防止过拟合,这里做进一步的简化,把 θ 0 ′ \theta_0' θ0′和 θ 1 ′ \theta_1' θ1′置为同一个值,只是取了个反,则有

最后这里的和单位阵相加可以简单的理解为加上一个自环,最终就很能得到本文开篇的GCN公式
3.基于message passing的图卷积
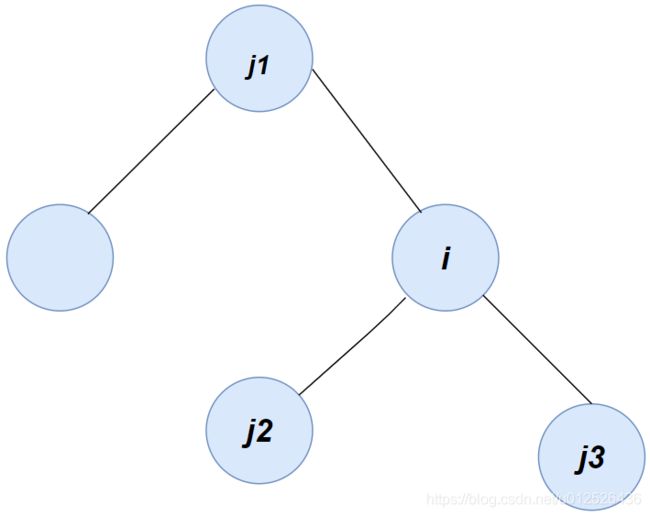
接下来我们从消息传递的角度解释下GCN,假如我们有这样一个图(该图是无向图),假如每个节点会互相给相邻节点传递消息,直到相邻节点的消息达到一个平衡状态,例如图中的 i i i节点,其有三个邻居节点 j n , n ∈ { 1 , 2 , 3 } j_n,n \in \{1,2,3\} jn,n∈{1,2,3},我们想计算出 i i i节点接收到的消息
注意我们这里的图需要遵循马尔科夫假设,根据上面的图我们可以得到 i i i节点的信息为
w ∑ j = 1 3 A i j ( x i − x j ) w\sum_{j=1}^3A_{ij}(x_i-x_j) wj=1∑3Aij(xi−xj)
其中 w w w表示的是邻节点传递给目标节点的一个传递系数, x n x_n xn表示 n n n节点的消息量, A A A表示的是邻接矩阵,因为是无向图邻接矩阵是对称阵,对角线上的值都是0,与其相邻的位置有非0的值,不相邻的位置值为0,所以上面的公式也说明只有相邻的节点才会有消息的传递,我们对上述公式简单的展开
w x i ∑ j = 1 3 A i j − w x j ∑ j = 1 3 A i j = w x i D i − w ∑ j = 1 3 A i j x j wx_i\sum_{j=1}^3A_{ij}-wx_j\sum_{j=1}^3A_{ij}=wx_iD_i-w\sum_{j=1}^3A_{ij} x_j wxij=1∑3Aij−wxjj=1∑3Aij=wxiDi−wj=1∑3Aijxj
如果用向量的形式来表示就是
w X D − w X A = w ( D − A ) X wXD - wXA=w(D-A)X wXD−wXA=w(D−A)X
细心的读者其实已经发现了,到这一步已经很接近GCN的计算公式了,唯一的区别就在于少了一个非线性的变化。
消息传递的核心思想就是把目标节点的邻居节点的消息就行一个聚合的操作,我们上面这里的公式可以把非线性变换看成是简单的求和(虽然这不是非线性的),当然你可以采用更多的聚合方式,例如平均,sigmoid,lstm,甚至使用attention机制计算加权平均。
4.GCN的效果与缺点
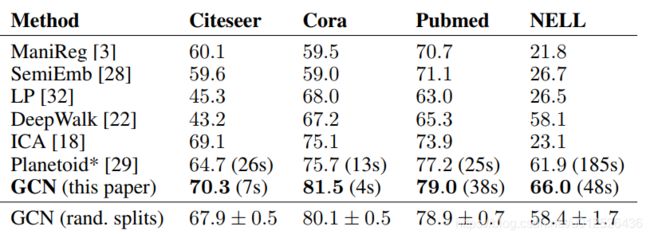
对比之前介绍过的DeepWalk模型,GCN整体的效果有较大的提升,并且保证了局部性、计算效率高等优势,但GCN也还存在一些缺点。
- 扩展性差:由于训练时需要需要知道关于训练节点、测试节点在内的所有节点的邻接矩阵 A A A,因此在扩展性问题上局限很大,每当图更新了就需要重新训练整个模型。
- 无法获取深层次特征:GCN论文中表明,目前GCN只局限于浅层,实验中使用2层GCN效果最好,加深模型层数需要使用残缺结构等trick,但是实际的效果提升并不明显。
- 不能处理有向图:拉普拉斯矩阵的特征分解需要满足拉普拉斯矩阵是对称矩阵的条件。
最后再上一张GCN和其他图模型的对比,可以看到,GCN的确还有很多进步空间,甚至在图像识别中效果甚至不如多层感知机,这也是因为其无法获取更深层次特征的原因。

看到着,有些读者可能会认为GCN效果这么差,为什么还要学习这个模型呢?其实其它的GNN模型中,其基本思想都和GCN中的message passing思想是类似的,所以我们需要对GCN先有一个大概的认识,这样对后续模型也能了解的更深入、透彻。
5.总结
本文对GCN的推导过程做了一个全面的介绍,相信阅读到这里的读者对GCN有了一个全面的认知,在阅读GNN方面的paper时肯定也会有更多的见解。本文部分细节内容没有深入讲解,读者如果想对例如傅里叶级数,傅里叶变换等内容有更深入的了解可以阅读reference中提到的博文。
6.References
1、图卷积网络 GCN Graph Convolutional Network(谱域GCN)的理解和详细推导
2、如何理解 Graph Convolutional Network(GCN)
3、Graph Neural Network (2/2) (助教姜成翰同學講授)
4、傅立叶及拉普拉斯
5、SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS