HED 和 RCF 图像边缘检测

HED 和 RCF 图像边缘检测

引言

虽然传统边缘检测算法在不断发展的过程中也取得了很大的进步，但仍然无法做到精细的边缘检测处理。随着近年来深度学习的快速发展，计算机视觉领域因此获益颇丰，当下最先进的计算机视觉应用几乎都离不开深度学习，深入我们生活的各个领域如目标检测、工业、农业、医疗等。由于深度学习的特性，使得它成为最适合处理计算机视觉任务的工具之一，特别是卷积神经网络(CNN)，得益于它强大的自动学习能力，图像边缘检测任务得到了长足的发展，涌现出了许多优秀的方法，如 N4-field、DeepContour、HED、RCF，基于神经网络的边缘检测算法成为了研究热点之一。

本文主要介绍基于 HED 网络的图像边缘检测的基本情况，对 HED 的网络架构和损失函数进行分析讨论。此外也将对另一个基于 HED 的网络，RCF 网络进行探究，对其进步之处进行分析。

HED 图像边缘检测

Holistically-Nested Edge Detection（简称 HED）由 Xie 等人提出。作为图像边缘检测领域一种比较经典的网络，HED 网络的出现对之后出现的各种图像边缘检测算法都有着启发式的贡献，解决了在计算机视觉领域存在的两个重要问题：

1. 基于整体图像的训练和预测；
2. 多尺度，多层次的特征学习。

在 HED 网络出现之前，大多数边缘检测方法如 N4-field、DeepEdge、DeepContour 等都是基于局部区域的算法。虽然通过 CNN 的学习能力上述方法也取得了不错的边缘检测性能，但也存在计算成本高，测试成本高的缺陷。而基于整体图像的训练和预测通过直接对图像中的每个像素进行判断，简单高效精确度高。

另外一方面，HED 网络拥有多个侧输出的单流深层网络，能够通过多尺度的学习，对中间细节进行丰富的特征提取。相比于直接利用输出层的最终结果，多尺度多层次的特征学习会拥有更好地边缘检测结果。

HED 网络架构

HED 网络架构建立在 VGG16 网络的基础之上，但做出了两方面的修改：

1. 为了进行多尺度多层次的特征学习，在 VGG16 网络每个阶段的最后一个卷积层（conv1_2,conv2_2，conv3_3，conv4_3，conv5_3）之后添加侧输出层。
2. 为了节约网络训练的内存/时间成本，去掉了最后一个池化层和之后的全连接层。

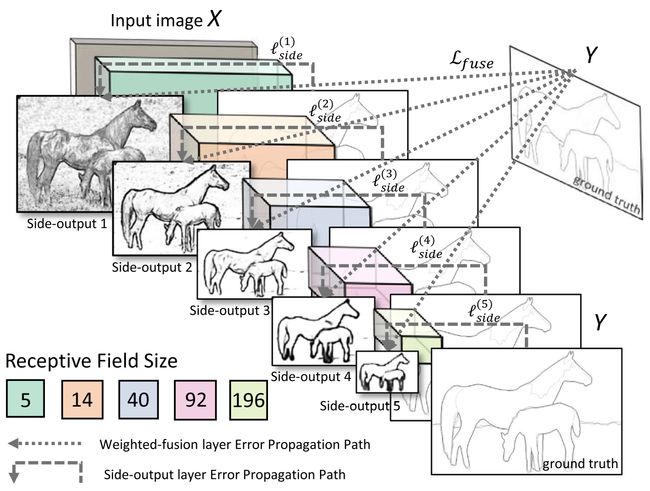
完整的网络结果如下图所示。通过将卷积层后引出的 5 个侧输出以及 5 个侧输出经过融合层后的结果同时进行训练，计算 6 个损失函数。通过多个侧输出，进行多尺度的学习，对中间细节进行特征提取。对于每个侧输出，通过双线性差值算法进行上采样，还原到原始图像的尺寸，通过融合层输出结果。

HED 损失函数

在 HED 网络中，损失函数由两部分共同构成：侧输出层的损失函数 ${\mathcal{L}}_{side}$ 和融合层的损失函数 ${\mathcal{L}}_{fuse}$。之后通过梯度下降法得到损失函数：

$$(W,w,h{)}^{\ast }=arg\min ({\mathcal{L}}_{side}(W,w)+{\mathcal{L}}_{fuse}(W,w,h))$$

其中 W 表示网络参数集合，w 表示侧输出层参数，h 表示融合权重。

（1）侧输出层的损失函数

HED 网络侧输出层的损失函数 ${\mathcal{L}}_{side}$ ：

$${\mathcal{L}}_{side}(W,w)=\sum _{m=1}^M{\alpha }_m{l}_{side}^{(m)}(W,w^{(m)})$$

其中 W 表示网络参数集合，w 表示侧输出层参数，M 表示侧输出层的数量，${\alpha }_m$ 表示每个侧输出层损失函数的权值。

HED 网络通过在每个像素项的基础上引入一个平衡权重 β，来自动平衡正负样本之间的损失。在边缘检测任务中，边缘像素在全部像素中所占的比例往往非常小，边缘像素和非边缘像素的不均衡对网络学习会产生非常严重的影响，导致最终结果检测出许多非边缘像素，平衡权重 β 的加入，正是为了解决这个问题。使用交叉熵损失函数。具体来说，若图像中边缘像素数量少，那么 β 值较小，第一项的权值较轻，而此项表示的是非边缘像素的损失，因此损失较小。

$$\begin{array}{rl}{\mathcal{L}}_{side}^{(m)}(W,w^{(m)})=& -\beta \sum _{j\in Y_{+}}\log Pr(y_j=1│X;W,w^{(m)})\\ & -(1-\beta )\sum _{j\in Y_{-}}\log Pr(y_j=0│X;W,w^{(m)})\end{array}$$

其中 $\beta =|Y_{-}|/|Y|$，$1-\beta =|Y_{+}|/|Y|$，Y 表示图像像素数量，$Y_{-}$和 $Y_{+}$ 分别表示边缘和非边缘像素数量。

（2）融合层的损失函数

为了利用侧输出预测，HED 网络通过权重融合层在训练期间同时学习融合权重。融合层的损失函数 ${\mathcal{L}}_{fuse}$ :

$${\mathcal{L}}_{fuse}(W,w,h)=Dist(Y,{\hat{Y}}_{fuse})$$

其中 ${\hat{Y}}_{fuse}\equiv \sigma ({\sum }_{m=1}^M{h}_m{\hat{A}}_{side}^{(m)})$，$\sigma (\cdot )$为激活函数，$h=(h_1,\cdots ,h_M)$表示融合权重。

HED 网络的优缺点

借助 VGG 网络强大的特征提取能力，HED 边缘检测算法能够对图像进行多尺度多层次的学习，直接对整幅图像进行操作。在侧输出层通过深度监督，将不同尺度的侧输出结果进行融合，最后得到了较为优秀的边缘检测结果。然而，随着网络深度的加深，深层特征的分辨率不断降低，导致了一些信息的丢失，在边缘的精细度方面有所欠缺。

RCF 图像边缘检测

在 HED 方法中只采用每个卷积阶段最后一层的卷积特征，而没有充分利用 CNN 丰富特性的层次结构。为了解决这一问题，Liu 等以 HED 网络为基础，提出了一种新的深层结构，Richer Convolutional Features，即更丰富的卷积特征（RCF）。RCF 通过自动学习将所有卷积层的信息组合起来，从而能够获得不同尺度的更加精细的特征。

RCF 网络架构

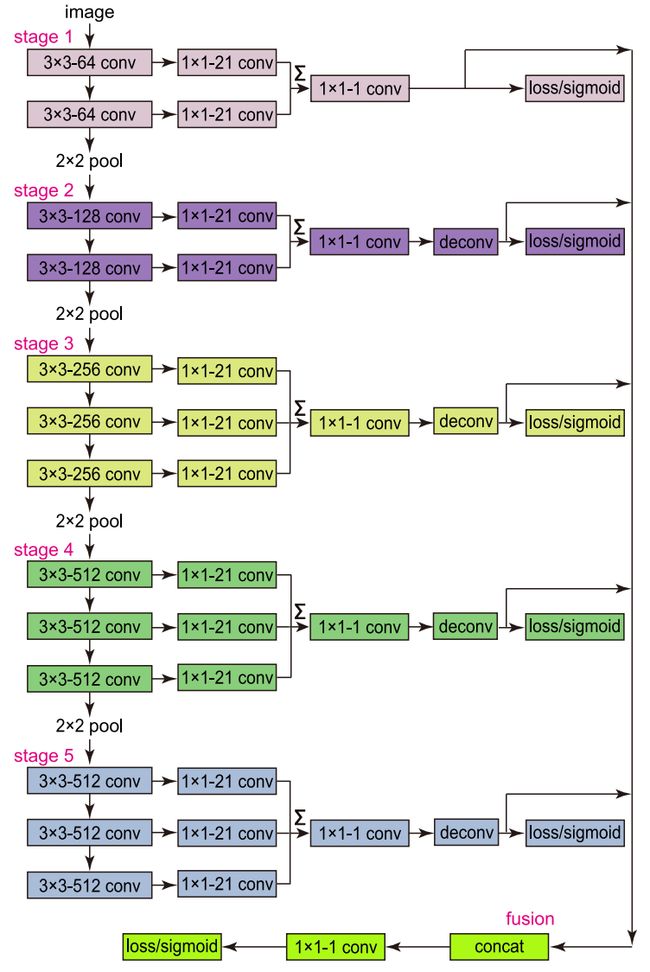
RCF 基于 HED 网络，与 VGG16 相比，RCF 主要做了如下修改：

1. 与 HED 相同，RCF 去掉了最后一个池化层和之后的全连接层，形成了全卷积网络。
2. 在 VGG16 的每个卷积层之后连接一个 1×1 大小深度为 21 的卷积层，并将每一阶段的特征累积得到混合特征。
3. 在每个阶段得到混合特征之后添加反卷积层进行上采样。
4. 在上采样层之后添加 loss/sigmoid 层计算损失。
5. 将所有上采用层连接，对每个阶段的特征进行融合，最后再通过 loss/sigmoid 层计算损失。

RCF 损失函数

与 HED 的做法类似，由于图像中边缘像素点和非边缘像素点的数量差异往往很大，需要计算正负样本之间的损失，RCF 对 HED 中的损失函数进行了改进，加入了阈值 $\eta$，若某个像素为边缘像素的概率小于阈值 $\eta$，则认为这个像素为非边缘像素:

$$l(X_i;W)=\{\begin{array}{ll}\alpha \cdot \log (1-P(X_i;W))& \text{if }{y}_i=0\\ 0& \text{if }0\le y_i\le \eta \\ \beta \cdot \log P(X_i;W)& \text{otherwise}\end{array}$$

其中

$$\alpha =\lambda \cdot \frac{|Y^{+}|}{|Y^{+}|+|Y^{-}|}$$

$$\beta =\lambda \cdot \frac{|Y^{-}|}{|Y^{+}|+|Y^{-}|}$$

$Y^{-}$和 $Y^{+}$分别表示边缘和非边缘像素数量，超参数 λ 用来平衡正负样本的数量，W 表示网络参数集合。RCF 改进的损失函数是：

$$L(W)=\sum _{i=1}^{|I|}\left(\sum _{k=1}^{K}l(X_i^{(k)};W)+l(X_i^{fuse};W)\right)$$

其中 $X_i^{(k)}$是阶段 k 的激活值，$X_i^{fuse}$ 是融合层的激活值。$|I|$是图像 I 的像素个数，K 是阶段数，这里为 5。

RCF 与 HED 的区别

HED 方法与 RCF 方法最大的区别在于以下两个方面：

1. HED 方法只考虑了 VGG16 网络每个阶段最后一个卷积层的特征，丢失了很多信息；而 RCF 网络充分考虑了 VGG16 网络的所有卷积层，从而能够获得更加丰富的信息，在几乎没有任何花费的情况下，大幅度提高了图像边缘检测的性能。

2. 新的损失函数。RCF 在 HED 损失函数的基础上进一步进行了修改，通过设置阈值 η 着重解决了多人标注情况下那些不确定是否为边缘的像素处理，提高了训练的稳定性。具体来说，RCF 将边缘像素概率高于阈值 η 的像素作为正样品，将边缘像素概率等于 0 作为负样本。而 HED 则设置阈值 η=0.5，并且将其作为正负样本的分界线。

参考文献

1. XIE S, TU Z. Holistically-Nested Edge Detection[J]. International Journal of Computer Vision, 2017, 125(1/3): 3–18.
2. LIU Y, CHENG M M, HU X 等. Richer Convolutional Features for Edge Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(8): 1939–1946.