机器学习——基本认识
一:机器学习定义
机器学习:Machine Learning
什么是机器学习?Arthur Samuel(机器学习领域的先驱之一,他编写了世界上第一个棋类游戏的人工智能程序)1959年对机器学习的定义:
Machine Learning is fields of study that gives
computers the ability to learn without being
explicitly programmed.
机器学习是这样的一个领域,它赋予计算机学习的能力,(这种学习能力)不是通过显著式编程获得的。
这里就涉及到了显著式编程的概念:
- 显著式编程:从一开始就定死了程序的输入和输出。
- 非显著式编程:让计算机自己总结规律的编程方法叫做非显著式编程。非显著式编程是让计算机通过数据、经验自动的学习完成我们交给的任务。
显著式编程是需要人为地根据周围的环境、规则、经验等给计算机规定一些机械化步骤或判断依据,比如需要人为规定黄色的是菊花,红色的是玫瑰,计算机就可以通过识别颜色来区别菊花和玫瑰花。
而非显著式编程无需人为给出所有的步骤和约束计算机必须总结什么规律,只需给计算机一堆菊花的图片与一堆玫瑰的图片,然后编写程序让计算机自己去总结菊花与玫瑰的区别,计算机很有可能通过大量的图片也能总结出菊花是黄色,玫瑰是红色这个规律,当然也有可能总结出菊花的花瓣是长的,玫瑰花瓣是圆的这些区别,我们把这种让计算机自己总结规律的编程方法叫做非显著式编程。
可见非显著编程更加灵活,适用范围更广。
另一个例子,假设我们要编程,让机器人到教室外面的咖啡机帮我们冲一杯咖啡:

显著式编程是这样的,首先我们要发指令给机器人,让他朝前走五步,然后左转走两步出门,然后再左转走五步来到咖啡机前:

然后发指令让机器人端起杯子到合适的位置,再按充咖啡的按钮,充好后再发指令让机器人原路返回。
我们可以看到这种显著式编程有很大的劣势,就是我们必须帮机器人把它所处的环境调查得一清二楚,而非显著式编程的优势就出来了。
非显著式编程是这样的,首先我们规定机器人可以采用一系列的行为,比如向左转向右转、前进后退等,我们规定在特定的环境下,机器人做这些行为所带来的收益,我们把它叫做收益函数,例如,如果机器人在采取某个行为导致自己摔倒了,那么我们的程序就要规定这个时候的收益函数值为负,如果机器人自己撞到了墙,也要规定收益函数值为负,如果机器人采取行为后取到了咖啡,那么程序就要奖励这个行为,把收益函数值设为正。我们规定了行为和收益函数后,让计算机自己去找最大化收益函数的行为,一开始,计算机采用随机化的行为,只要我们程序编写的足够好,计算机是可能找到一个最大化收益函数的行为模式的。
可以看出,非显著式编程可以通过数据、经验自动的学习完成我们交给的任务。
而机器学习的第二个定义出自Tom Mitshell在1998年编写的书《Machine Learning》,我们公认这本书是机器学习领域第一本成熟的教科书,定义如下:
A computer program is said to learn from experience E with respect to some task T
and some performance measure P,if its performance on T ,as measured by P,improves
with experience E.
一个计算机程序被称为可以学习,是指它能够针对某个任务T和某个性能指标P,
从经验E中学习。这种学习的特点是,它在T上的被P所衡量的性能,会随着经验E的增加而提高。
在菊花和玫瑰案例中,
- 任务T就是编写计算机程序识别菊花和玫瑰
- 经验E就是一大堆菊花和玫瑰的图片,在机器学习中,这些图片被称为训练样本
- 性能指标P不同的机器学习算法会有不同,在这里我们使用最常规的识别率(Recognition Rate)为例,即让更多的菊花被识别成菊花,更多的玫瑰被识别成玫瑰,把识别的正确率简称识别率,作为性能指标
据Tom Mitshell的定义,机器学习就是根据识别菊花和玫瑰这样的任务,构造某种算法,这种算法的特点是,当训练的菊花和玫瑰图片越来越多的时候,识别率也会越来越高
明显显著式编程是无法达到这一目的的,因为其一开始就定死了输入和输出,识别率不会随着训练样本增加而变化
在机器人充咖啡案例中
- 任务T就是设计程序让机器人充咖啡
- 经验E就是机器人多次尝试的行为和这些行为产生的结果
- 性能指标P就是在规定时间内成功充好咖啡的次数
可见Tom Mitshell的定义比Arthur Samuel更加数学化,根据经验E来提高性能指标P的过程是典型的最优化问题,数学中各种最优化方法都可以应用其中,数学在现代机器学习中占有重要的作用。
问题:以下四个机器学习任务的经验E是什么?性能指标P又是什么?注:经验E和性能指标P是由设计算法的人设计的,没有标准答案
- 教计算机下棋
- 垃圾邮件识别,教计算机自动识别某个邮件是垃圾邮件
- 人脸识别,教计算机通过人脸的图像识别这个人是谁
- 无人驾驶,教计算机自动驾驶汽车从一个指定地点到另一个指定地点
答(本人没有答案,以下作答是个人看法,欢迎大佬评论区指正):
1. 教计算机下棋
E:棋谱棋局、机器人多次尝试的棋路和这些行为产生的结果
P:胜率、规定时间内优胜次数
2. 垃圾邮件识别,教计算机自动识别某个邮件是垃圾邮件
E:正常邮件与垃圾邮件
P:识别率
3. 人脸识别,教计算机通过人脸的图像识别这个人是谁
E:人的身份与人脸图片
P:识别率
4. 无人驾驶,教计算机自动驾驶汽车从一个指定地点到另一个指定地点
E:无人汽车多次尝试的行为和这些行为产生的结果
P:规定时间内到达指定地点的次数
二:机器学习的分类
我们可以对上面4个机器学习任务进行分类,即14是同一类,23是同一类,而划分标准就是经验E:
- 垃圾邮件和人脸识别的经验E完全是由人搜索起来输入进计算机。告诉计算机哪些是垃圾邮件,哪些是正常邮件,以及告诉计算机那些人脸属于谁的过程,被称为为训练数据打标签(Labeling for training data),因此23的经验E就是训练样本和标签的集合,我们把这一类输入计算机数据并加上标签的机器学习称为监督学习(Supervised Learning)
- 在教计算机下棋(可以由人输入经验,这里只是为了说明两种学习区别,因此不对案例本身做严格讨论)和自动驾驶中,经验E是由计算机与环境互动获得的,计算机产生行为,同时获得行为的结果,程序只需要定义这些行为的收益函数(Reward function)对行为进行奖励和惩罚,并通过改变自己的行为模式去最大化收益函数。我们把这一类计算机通过与环境的互动逐渐强化自己的行为模式的机器学习叫做强化学习(Reinforcement Learning)
总结起来,根据任务性质的不同,我们可以把机器学习算法分为监督学习和强化学习两类,当然这种分类并不绝对,现代的强化学习中也用到了监督学习的方法,例如围棋程序 alpha go ,这是典型的强化学习任务,但在最初的alpha go的训练是用到了高手的对局进行监督学习,利用监督学习获得初始围棋程序,然后再对初始围棋程序进行监督学习以强化棋力,这是监督学习与强化学习结合的典型例子。
对于监督学习,我们还可以根据数据标签存在与否的分类分成三类:
- 传统的监督学习(Traditional Supervised Learning):每一个数据都有对应的标签,在传统的监督学习中,我们要学的算法如下:
- 支持向量机(support vector machine)
- 人工神经网络(neural networks)
- 深度神经网络(deep neural networks)
- 非监督学习(Unsupervised Learning):所有的数据都没有对应的标签,在非监督学习中,我们要学的算法如下:
- 聚类(clustering)
- EM算法(Expectation-Maximization algorithm)
- 主成分分析(principle component analysis)
- 半监督学习(Semi-supervised Learning):训练数据中一部分有标签,一部分没有标签。
对于非监督学习,如果所有数据都没有标签,那怎么获取类别信息呢?下面是一个例子:
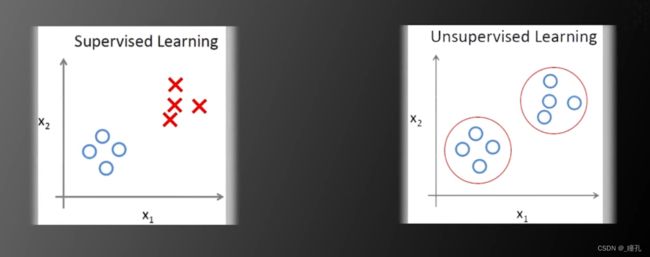
左边图片中,圆圈代表一类,X代表一类,但在右边的图片中,我们有这些训练数据,但不知道训练数据的类别,那么应该如何分类呢,我们需要假设同一类的训练数据在空间中距离更近,如果这个假设成立,那么我们可以根据样本的空间信息设计算法将他们聚集分为两类,从而实现没有标签的机器学习,即无监督学习
在如今,半监督学习获得了越来越多的关注,因为随着互联网的普及,网络中存在大量的数据,但是标注数据是成本巨大的工作,研究使用少量的标注数据和大量的无标注数据一起训练更好的机器学习算法成为了机器学习领域热点之一。以下是一个半监督学习例子:
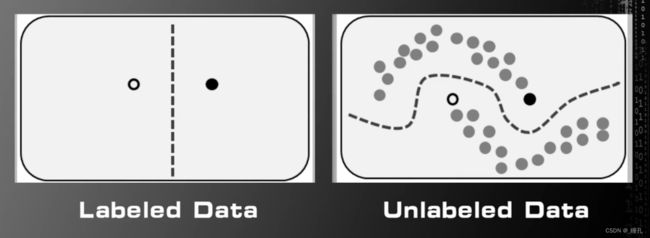
左边只有两个标注过的训练样本,我们并不知道如何进行分类,但是如果我们增加一些没有标签的训练样本,如右图所示,那么我们有可能设计算法更准确的实现分类
对于监督学习,除了根据数据标签存在与否分类,我们还可以根据数据标签是连续还是离散分类:
- 分类(classification):标签是离散的值
- 回归(regression):标签是连续的值
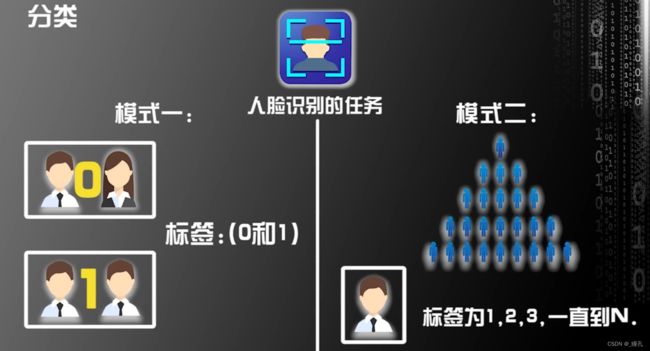
人脸识别就是分类问题,人脸识别的任务有两种模式,第一种模式是识别两张人脸是不是同一个人,我们可以把是同一个人的标签设为1,不是同一个人的标签设为0,可见标签是离散的,即0和1。人脸识别的第二种模式是识别人脸是一堆人中的哪一个人,假设有n个人,每个人都有自己特定的标签,从1、2、3一直到n,可见标签也是离散的数值
设计算法预测房价走势就是回归问题,下面是2014到2015年上海的房价走势,这里的训练样本是时间,而平均房价就是标签,平均房价是连续的变量,可见这是一个回归问题。同样,预测股票价格、预测问题、预测人的年龄等任务都是回归问题

对于房价我们还可以这么理解,把房价四舍五入精确到一元,那么房价也可以说是离散的,其实分类和回归问题的界限是非常模糊的,因为连续和离散的定义也是可以相互转换的,因此一个解决分类问题的机器学习模型,稍微加以改造,就可以解决回归问题,反之亦然。
三:机器学习算法的过程
下图是基于SVM的尿沉渣红、白细胞识别的课程作业

当我们拿到数据之后,构建机器学习算法的第一步是观察数据,总结规律,提取特征。值得一提的是,最近几年,由于大数据和深度学习的发展,很多人会认为只要收集足够多的数据,从网上随便下载一个开元的训练模型,将数据扔进模型中训练,就可以获得很好的结果,但是通常情况下这种想法是不正确的。如果我们自己对数据没有感性的认识,就很难设计出好的算法,也就很难估计算法达到的性能极限。
观察图片,我们可能观察到的红、白细胞的区别:
- 平均来说,白细胞面积比红细胞大;
- 白细胞没有红细胞圆;
- 白细胞内部纹理比红细胞粗糙。
机器学习算法过程第一步:提取特征(Feature Extraction),是指通过训练样本获得的,对机器学习任务有帮助的多维度的特征数据,而对于上述作业,我们可以提取三个特征:细胞的面积、圆形度、表面粗糙程度
提取三种特征的方法:为了提取面积特征,采用了图像处理中的链码提取细胞的边缘信息,从细胞边缘信息推测细胞周长和面积,同时通过细胞边缘信息使用图像处理中的哈弗变换(Hough Transform)提取细胞的圆形程度,用灰度共生矩阵提取细胞的粗糙程度

需要强调的是,机器学习的重点不是提取特征,而是假设在已经提取好特征的前提下,如何构造算法获得更好的性能,当然这不是说提取特征不重要,好的特征能有效提高模型效率,那为什么提取特征不是机器学习的重点呢?因为不同的任务提取特征的方式也不同,例如图像、语音,这些媒质的特征各不相同,同时机器学习的任务也各不相同,因此针对不同的媒质不同的任务,提取特征的方式千变万化,因此机器学习会缩小研究范围,在假设已经获得特征的前提下研究合理的算法,使学习系统获得较好的性能
机器学习算法过程第二步:特征选择(feature selection),在这一步需要对特征进行取舍。下图中,可见在面积和周长的特征中,区别白细胞和红细胞的准确度是非常高的,因为重合部分很少,而在圆形度上,尽管红细胞平均值较高,但红白细胞有较多的重合,因此如果使用圆形度区分红白细胞,那么准确率不会很高。

而对纹理特征做了如下分析,可见即使部分特性红白细胞是有所区别的,但整体区分度仍然不如面积与周长
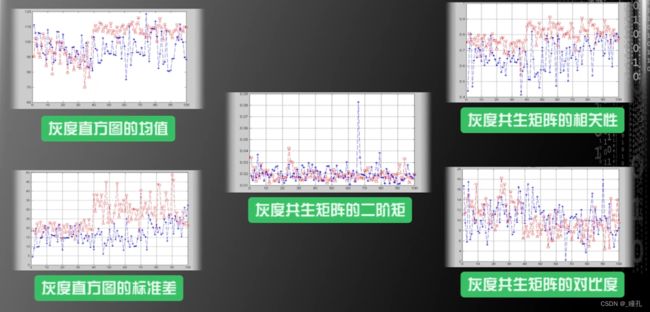
因此可以只选择面积和周长作为区分红、白细胞的特征来构建机器学习系统

那么如何基于这两个特征构建算法呢,这里采用的是支持向量机算法,用到了支持向量机的三种内核:线性内核、多项式内核和高斯径向基函数核
训练结果如下,图中横坐标代表面积,纵坐标代表周长,我们把这两个特征组成的二维平面叫做特征空间(feature space),在这个例子中,特征空间是二维的,如果有两个以上的特征,特征空间的维度是可以高于二维。以下三张图中的分割线是分别采用不同的支持向量机内核所计算出的,一旦画出这根线,机器学习的过程就算完成了

因此总结来说,机器学习算法的过程:
特征提取、特征选择 ——> 不同的算法对特征空间做不同的划分 ——> 获得不同的结果
四:没有免费午餐定理
1995年,D.H.Wolpert等人提出没有免费午餐定理(No Free Lunch Theorem),定理的内容是:任何一个预测函数,如果在一些训练样本上表现好,那么必然在另一些训练样本上表现不好,如果不对数据在特征空间的先验分布有一定假设,那么表现好与表现不好的情况一样多
注:先验分布(prior distribution)一译“验前分布”“事前分布”。是概率分布的一种。与“后验分布”相对。与试验结果无关,或与随机抽样无关,反映在进行统计试验之前根据其他有关参数θ的知识而得到的分布。
以计算机为例,假设只有两个存储单元,当然,只是假设,每个存储单元要么属于第一类,要么属于第二类,用O代表第一类,用X代表第二类,这是一个两类的分类问题,假设我们知道一个存储单元的类别是O,那么我们要预测另一个存储单元的类别。
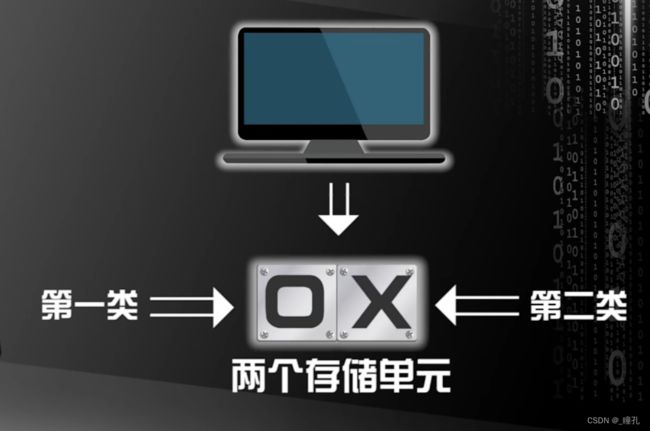
这个预测有两种情况,两个存储单元是O,以及第一个存储单元是O,第二个是X,如果我们事先不假定两者的先验概率分布,那么一个合理的假设是,这两种情况的概率相同,都是50%,在这种情况下不管我们是预测第二个单元是O还是X都是对错各一半概率
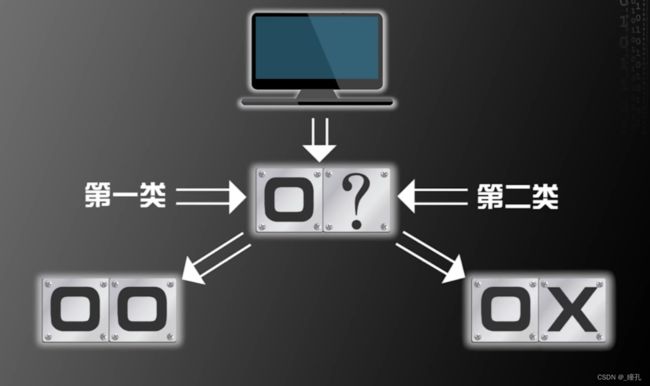
那么,现在假设计算机有三个存储单元,已知第一个存储单元是O,那么另外两个存储单元是什么呢?

现在有四种可能,预测第二个单元是O有两种可能,是X的也有两种可能,第三格单元同理。所以第二个单元和第三个单元预测成功的概率都是50%

那么如果知道更多的情况,结果会不会好一点呢?现在假设已知第一个和第二个存储单元都是O,那么第三个存储单元是什么呢?如果第三个单元为O或者X的概率相等,那么成功预测的概率仍然是50%

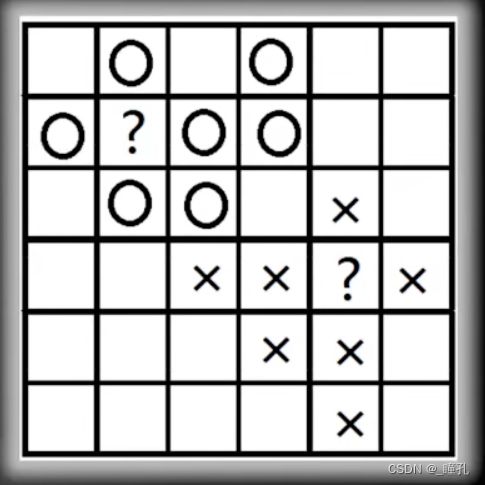
运用这样的推理,我们可以知道,无论计算机的存储单元有多少个,无论我们知道多少个存储单元的类别,对剩下单元的预测,结果都是对错各50%概率,此时不论是什么算法,还是我们自己盲猜,成功预测的概率都是一样的,那么问题出在哪呢?是假设出了问题,之前都是假设各种情况下先验概率一样,可以看下图如果计算机的存储空间是6*6的格子,相信大多数人都会预测上面的未知单元为O,下面的未知单元为X,事实上,目前流行的所有机器学习算法都会这么预测,这是因为我们在设计机器学习算法时有这样一个假设:在特征空间上距离接近的样本,他们属于同一个类别的概率会更高。
没有免费午餐定理告诉我们,不对特征空间的先验分布有假设,那么所有算法的表现都是一样的,我们不能片面夸大这个定理的作用,从而对开发新的算法丧失信息,但是我们也要时刻牢记这个定理的提醒,机器学习的本质是通过有限的已知数据,在复杂的高维特征空间中预测未知的样本,然而我们并不知道未知样本的性质如何,因此再好的算法也存在犯错的风险。另一方面,没有免费午餐定理告诉我们没有放之四海而皆准的最好算法,因为评价算法的好坏涉及到对特征空间先验分布的假设,然而没有人知道特征空间先验分布真实的样子
如果有兴趣了解更多相关内容,欢迎来我的个人网站看看:瞳孔的个人网站
