十大算法之SVM

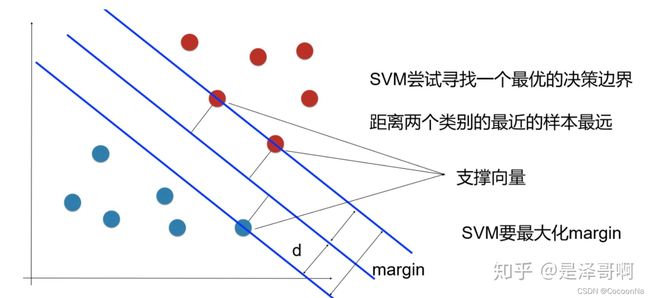
支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，**基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。**可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

“硬间隔”与“软间隔”
硬间隔容易被个别少数点所影响，其较为严格规定范围

概念解析：凸二次规划

凸二次规划问题：当目标函数是二次型函数且不等式约束函数 g 是仿射函数时，就变成一个凸二次规划问题。
目标函数f是二次型函数函数。如svm

学习地址：https://zhuanlan.zhihu.com/p/31886934
学习地址：https://zhuanlan.zhihu.com/p/77750026

概念解析：鲁棒性

指控制系统在一定参数摄动下，维持其它某些性能的特性

疑问

因为我们希望最小化 [公式] ，梯度 [公式] (函数 [公式] 在点 [公式] 的最陡上升方向)应该指向可行域 [公式] 的内部(因为你的最优解最小值是在边界取得的)，但 [公式] 指向 [公式] 的外部(即 [公式] 的区域，因为你的约束是小于等于0)，因此 [公式] ，称为对偶可行性(dual feasibility)。

KKT学习（不等式约束）

参考地址：https://zhuanlan.zhihu.com/p/38163970

SMO

SMO(Sequential Minimal Optimization)，序列最小优化算法，其核心思想非常简单：每次只优化一个参数，其他参数先固定住，仅求当前这个优化参数的极值。

松弛变量与惩罚因子

学习地址：https://blog.csdn.net/qll125596718/article/details/6910921

概念解析：对偶问题

任何一个求极大化的线性规划问题都有一个求极小化的线性规划问题与之对应，反之亦然，如果我们把其中一个叫原问题，则另一个就叫做它的对偶问题，并称这一对互相联系的两个问题为一对对偶问题。

核函数

对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。

支持向量机目前只适合小批量样本的任务，无法适应百万甚至上亿样本的任务。

！！！实战！

参考地址：https://blog.csdn.net/hahaha66888/article/details/87920086

Panda库的使用

①：读取csv类型文件的内容

two = pandas.read_csv('two.csv') 

② Series
Series是一种类似于一维数组的对象，它由一组数据（各种NumPy数据类型）以及一组与之相关的数据标签（即索引）组成，即index和values两部分，可以通过索引的方式选取Series中的单个或一组值。

pd.Series(list,index=[ ])，第二个参数是Series中数据的索引，可以省略。
第一个参数可以是字典，字典的键将作为Series的索引
第一个参数可以是DataFrame中的某一行或某一列

③ DataFrame的建立
DataFrame是一个表格型的数据类型，每列值类型可以不同，是最常用的pandas对象。
DataFrame既有行索引也有列索引，它可以被看做由Series组成的字典（共用同一个索引）。
DataFrame中的数据是以一个或多个二维块存放的（而不是列表、字典或别的一维数据结构）。

pd.DataFrame(data,columns = [ ],index = [ ])：columns和index为指定的列、行索引，并按照顺序排列。

import pandas as pd
data = {'state': ['Ohio', 'Ohio', 'Ohio', 'Nevada', 'Nevada', 'Nevada'],
        'year': [2000, 2001, 2002, 2001, 2002, 2003],
        'pop': [1.5, 1.7, 3.6, 2.4, 2.9, 3.2]}
df= pd.DataFrame(data)
In [45]: df
Out[45]: 
   pop   state  year
0  1.5    Ohio  2000
1  1.7    Ohio  2001
2  3.6    Ohio  2002
3  2.4  Nevada  2001
4  2.9  Nevada  2002
5  3.2  Nevada  2003

data.index返回一个index类型的行索引列表，data.index.values返回的是行索引组成的ndarray类型。

data.columns返回一个index类型的列索引列表，data.columns.values返回的是列索引组成的ndarray类型。

一个 **ndarray(n维数组）**是具有相同类型和大小的项目的（通常是固定大小的）多维容器。 尺寸和数组中的项目的数量是由它的shape定义， 它是由N个非负整数组成的tuple（元组），用于指定每个维度的大小。 数组中项目的类型由单独的data-type object (dtype)指定， 其中一个与每个ndarray相关联。

print(two.head(3))  #参数为样本数量的前3行
print(two.tail(3))  #参数为样本数量的后3行

参考地址：https://blog.csdn.net/Droke_Zhou/article/details/87306785

④ pandas.DataFrame.corr: 用于查找数据帧中所有列的成对相关性

df.corr()

复习map函数的用法

map() 会根据提供的函数对指定序列做映射。
第一个参数 function 以参数序列中的每一个元素调用 function 函数，返回包含每次 function 函数返回值的新列表。

>>> def square(x) :         # 计算平方数
...     return x ** 2
...
>>> map(square, [1,2,3,4,5])    # 计算列表各个元素的平方
<map object at 0x100d3d550>     # 返回迭代器
>>> list(map(square, [1,2,3,4,5]))   # 使用 list() 转换为列表
[1, 4, 9, 16, 25]
>>> list(map(lambda x: x ** 2, [1, 2, 3, 4, 5]))   # 使用 lambda 匿名函数
[1, 4, 9, 16, 25]
>>>

https://blog.csdn.net/hahaha66888/article/details/87920086
https://blog.csdn.net/qq_45261963/article/details/118324085

学习Seaborn库

参考地址：https://www.cnblogs.com/cymx66688/p/10536403.html
countplot是seaborn库中分类图的一种，作用是使用条形显示每个分箱器中的观察计数。
x: x轴上的条形图，以x标签划分统计个数

y: y轴上的条形图，以y标签划分统计个数

hue(色调）: 在x或y标签划分的同时，再以hue标签划分统计个数

order, hue_order : lists of strings, optional.Order to plot the categorical levels in, otherwise the levels are inferred from the data objects.
order, hue_order分别是对x或y的字段排序，hue的字段排序。排序的方式为列表。
sns.countplot(x=‘class’, data=titanic, order=[‘Third’, ‘Second’, ‘First’])

HeatMap热力图：热力图在实际中常用于展示一组变量的相关系数矩阵，在展示列联表的数据分布上也有较大的用途，通过热力图我们可以非常直观地感受到数值大小的差异状况。

annot：annotate的缩写，annot默认为False，当annot为True时，在heatmap中每个方格写入数据

参考地址：https://blog.csdn.net/m0_38103546/article/details/79935671
参考地址：https://zhuanlan.zhihu.com/p/96040773?from_voters_page=true

学习plt.figure()

figure语法及操作
figure(num=None, figsize=None, dpi=None, facecolor=None, edgecolor=None, frameon=True)

num:图像编号或名称，数字为编号 ，字符串为名称
figsize:指定figure的宽和高，单位为英寸；
dpi参数指定绘图对象的分辨率，即每英寸多少个像素，缺省值为80 1英寸等于2.5cm,A4纸是 21*30cm的纸张
facecolor:背景颜色
edgecolor:边框颜色
frameon:是否显示边框

import matplotlib.pyplot as plt
创建自定义图像
fig=plt.figure(figsize=(4,3),facecolor='blue')
plt.show()

特征选择

特征选择的目的是降维，用少量的特征代表数据的特性，这样也可以增强分类器的泛化能力，避免数据过拟合。

可以从相关性大的的每类属性中任意选一个作为代表，（热力图中颜色越浅相关性越大）

！！from sklearn.cross_validation import train_test_split，train_test_split下出现红色波浪线

解决方法：https://blog.csdn.net/littlle_yan/article/details/83656662

数据预处理——标准化/归一化

from sklearn.preprocessing import MinMaxScaler,StandardScaler,MaxAbsScaler,RobustScaler

如果要做中心化处理，并且对数据分布有正态要求，那么使用Z-Score方法
如果要进行0-1标准化或者将要指定标准化后的数据分布范围，那么使用Max-Min标准化或MaxAbs标准化方式是比较好的方法，尤其是前者。
如果要对稀疏数据进行处理，Max-Min标准化或者MaxAbs标准化是理想方法
如果要最大限度保留数据集中的异常，那么使用RobustScaler方法更好
  大多数机器学习算法中，会使用Z-Score方法来对特征进行标准化。因为Max-Min标准化对异常值特别敏感。一般情况下，都会使用Z-Score标准化，如果要指定标准化后的数据分布范围，那么使用Max-Min标准化。