特征工程:特征处理
数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已;
好的特征不仅能够表示出数据的主要特点,还应该符合模型的假设;
特征越好、灵活性越强,构建的模型越简单、性能越出色。
特征工程是从原始数据提取特征的过程,这些特征可以很好地描述数据,并且利用特征建立的模型在未知数据上的性能表现可以达到最优。特征工程一般包括特征使用、特征获取、特征处理、特征选择和特征监控。
特征处理的方法主要有特征缩放、连续型变量离散化、One-Hot编码等方法。
1 特征缩放
特征缩放会改变特征的尺度。机器学习中的一些算法是输入的平滑函数,比如线性回归模型、逻辑回归模型等,这些模型会受到输入尺度的影响。所以需要进行特征缩放。
1.1 标准化
标准化是依照特征矩阵的列处理数据,即通过求标准分数的方法,将特征转换为标准正态分布,并和整体样本分布相关。每个样本点都能对标准化结果产生影响。其转换公式如下: x ′ = x − X ‾ S x^{'}=\frac{x-\overline X}{S} x′=Sx−X其中 X ‾ \overline X X为特征 x x x的均值, S S S为特征 x x x的标准差。
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
iris=load_iris()
X=iris.data
X_df=pd.DataFrame(X,columns=iris.feature_names)
X_new=pd.DataFrame(StandardScaler().fit_transform(X_df),
columns=iris.feature_names)
"""
StandardScaler()中的fit_transform()和fit()方法中的X只能接受二维数据,
所以在对单个特征进行处理的时候需要注意。
若是DataFrame型变量也是直接使用原始公式进行转换。
"""
X_new_2=pd.DataFrame(None)
X_new_3=pd.DataFrame(None)
for i,col in enumerate(X_df.columns):
X_new_2[col]=(X_df[col]-X_df[col].mean())/X_df[col].std()
tmp=StandardScaler().fit_transform(X[:,[i]])
X_new_3[col]=tmp.flatten()
若数据中存在异常值,可能会影响平均值和方差,影响标准化结果。在此种情况下,使用中位数和四分位数间距进行缩放会更有效。
from sklearn.preprocessing import RobustScaler
from sklearn.datasets import load_iris
X=load_iris().data
X_new=RobustScaler().fit_transform(X)
1.2 区间缩放法(最大最小归一化)
区间缩放法常见的是利用两个最值(最大值和最小值)进行缩放。其公式为: x ′ = x − x m i n x m a x − x m i n x^{'}=\frac{x-x_{min}}{x_{max}-x_{min}} x′=xmax−xminx−xmin其中 x m a x x_{max} xmax和 x m i n x_{min} xmin为特征 x x x的最大值和最小值。
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
iris=load_iris()
X=iris.data
X_df=pd.DataFrame(X,columns=iris.feature_names)
X_new=pd.DataFrame(MinMaxScaler().fit_transform(X),
columns=iris.feature_names)
#针对单个字段的变换
X_new_2=pd.DataFrame(None)
X_new_3=pd.DataFrame(None)
for i,col in enumerate(X_df.columns):
X_new_2[col]=(X_df[col]-X_df[col].min())/(X_df[col].max()-X_df[col].min())
tmp=MinMaxScaler().fit_transform(X[:,[i]])
X_new_3[col]=tmp.flatten()
1.3 归一化
归一化是将样本的特征值转换到统一量纲下,将数据映射到 [ 0 , 1 ] [0,1] [0,1]或着 [ a , b ] [a,b] [a,b]区间内。归一化会改变数据的原始距离、分布和信息。使用 L 2 L2 L2范数的归一化公式如下: x ′ = x x 1 2 + x 2 2 + ⋯ + x m 2 x^{'}=\frac{x}{\sqrt{x_{1}^{2}+x_{2}^{2}+\dots+x_{m}^{2}}} x′=x12+x22+⋯+xm2x
from sklearn.datasets import load_iris
from sklearn.preprocessing import Normalizer
iris=load_iris()
X=iris.data
X_new=Normalizer().fit_transform(X)
X_new_2=[]
for i in range(X.shape[0]):
tmp=X[i]/np.sqrt(np.sum(np.square(X[i])))
X_new_2.append(tmp)
X_new_2=np.array(X_new_2)
#X_new和X_new_2中每一行数据的平方和为1
tmp=np.sum(np.square(X_new),axis=1)
tmp_2=np.sum(np.square(X_new_2),axis=1)
tips: sklearn中的Normalizer()可以通过参数norm选择不同的归一化公式,具体有三种方式可选:‘l1’, ‘l2’(默认值), ‘max’。
归一化和标准化、区间缩放法的不同在于,标准化和区间缩放法是针对每一个特征做的,而归一化是针对数据的行做的。经过归一化之后,特征列的范数就是1(目前在机器学习算法中很少看到这一种方法的使用)。
1.4 使用场景
区间缩放法是归一化的一种特例,所以在很多材料里也把区间缩放法称为归一化方法(以下所说的归一化方法是指区间缩放法)。归一化和标准化的应用场景如下:
- 如果对输出结果范围有要求,则用归一化。
- 如果数据较为稳定,不存在极端的最大值和最小值,则用归一化。
- 如果数据存在异常值和较多噪声,则用标准化,这样可以通过中心化间接避免异常值和极端值的影响。
- 在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,标准化表现更好。
- 支持向量机,K近邻、主成分分析都模型都必须进行归一化或标准化操作。主要是因为这些模型在各个维度进行不均匀伸缩后,最优解与原来不等价。
- 在“稀疏”特征上归一化和标准化时一定要注意,它们都会从原始特征上减去一个平移量。如果这个平移量不是0,那么这两种变换会将一个多元素为0的的稀疏特征向量变成密集特征向量,这种改变会给分类器带来巨大的计算负担。
1.5 总结和实现
对特征进行缩放可以带来几个优势:
- 提高模型收敛速度(比如,可以加快梯度下降法的求解速度)。
- 在一些涉及欧式距离计算的算法中,归一化可以提升模型精度。
- 衡量各特征对结果影响程度时必须要归一化。
- 深度学习中数据归一化可以防止模型梯度爆炸。
实现
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
X,y=make_regression(n_samples=1000,n_features=2,n_informative=2,
noise=10,n_targets=1,random_state=0)
#人为调整第二个变量的取值范围,作为归一化之前的数据 X为归一化之后的数据
X_new=X.copy()
X_new[:,1]=X_new[:,1]*5+100
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,
random_state=0)
X_train_new=X_train.copy()
X_train_new[:,1]=X_train_new[:,1]*5+100
X_test_new=X_test.copy()
X_test_new[:,1]=X_test_new[:,1]*5+100
#验证模型收敛速度(使用梯度下降法)
def L_theta(theta, X_x0, y,):
h = np.dot(X_x0, theta) # np.dot 表示矩阵乘法、
theta_without_t0 = theta[1:]
L_theta = 0.5 * mean_squared_error(h, y)
return L_theta
# 梯度下降
def GD(lamb,X_x0, theta, y, alpha):
m=X_x0.shape[0]
result=[]
for i in range(T):
h = np.dot(X_x0, theta)
theta_with_t0_0 = np.r_[np.zeros([1, 1]), theta[1:]]
theta -=(alpha * 1/m * np.dot(X_x0.T, h - y) + lamb*(theta_with_t0_0))
if i%5000==0:
result.append(L_theta(theta, X_x0, y))
return theta,result
T = 120000 # 迭代次数
theta = np.ones((3, 1)) # 参数的初始化,degree = 11,一个12个参数
alpha = 0.000005
lamb = 0.000001
X_x0=np.c_[np.ones((X.shape[0],1)),X]
y_y0=y.reshape(-1,1)
theta,result= GD(lamb=lamb,X_x0=X_x0, theta=theta, y=y_y0, alpha=alpha)
X_new_x0=np.c_[np.ones((X_new.shape[0],1)),X_new]
theta_new = np.ones((3, 1))
theta_new,result_new = GD(lamb=lamb,X_x0=X_new_x0, theta=theta_new, y=y_y0, alpha=alpha)
plt.plot(result,label='after normalizer')
plt.plot(result_new,label='before normalizer')
plt.legend()
plt.ylabel("MSE")
plt.show()
##分别对两组数据训练模型
lr=LinearRegression()
lr.fit(X_train,y_train)
y_test_pred=lr.predict(X_test)
score,mse=r2_score(y_test,y_test_pred),mean_squared_error(y_test,y_test_pred)
print("归一化之后模型的准确率: R2为{:.3f},MSE为{:.3f}".format(score,mse))
print("归一化之后模型的参数重要性依次为:{:.3f},{:.3f}".format(lr.coef_[0],lr.coef_[1]))
print("归一化之后模型的截距为:{:.3f}".format(lr.intercept_))
lr=LinearRegression()
lr.fit(X_train_new,y_train)
y_test_pred_new=lr.predict(X_test_new)
score,mse=r2_score(y_test,y_test_pred),mean_squared_error(y_test,y_test_pred)
print("归一化之前模型的准确率: R2为{:.3f},MSE为{:.3f}".format(score,mse))
print("归一化之前模型的参数重要性依次为:{:.3f},{:.3f}".format(lr.coef_[0],lr.coef_[1]))
print("归一化之前模型的截距为:{:.3f}".format(lr.intercept_))
(1) 在相同迭代次数下,归一化之后其收敛速度更快,具体如下图:

(2) 虽然模型效果并没有下降,但归一化之后特征的参数发生了变化。具体结果如下 :
归一化之后模型的准确率: R2为0.973,MSE为88.592
归一化之后模型的参数重要性依次为:40.455, 40.700
归一化之后模型的截距为:-0.410
归一化之前模型的准确率: R2为0.973,MSE为88.592
归一化之前模型的参数重要性依次为:40.455, 8.140
归一化之后模型的截距为:-814.418
2.交互特征/多项式特征
两个或两个以上特征的乘积可以组成一对简单的交互式特征。sklearn中提供了专门的类来构造交互式特征,具体如下:
![]()
其中几个参数的作用如下:
- degree: 多项式特征的度数。可以理解为最多可以使用多少个特征进行乘积操作(若一个特征出现不止一次,则按多次计算)。
- interaction_only: 是否仅产生交互式特征。如果为True,则每一个组合成的多项式特征中任意一个特征最多只能出现一次。比如,有两个特征 x 1 x_{1} x1和 x 2 x_{2} x2,当degree=2时,该类形成的特征中不包括 x 1 2 x_{1}^{2} x12和 x 2 2 x_{2}^{2} x22。
- include_bias: 是否产生偏差列。当为True时,会增加一个值为1的常数列。
类的属性:
- powers_:返回一个n_output_features_ ∗ * ∗n_input_features_的array,说明每一个输出变量的计算来源。举例,power[i]=[1,0,2,0],则说明第 i i i个输出变量 = x 0 1 ∗ x 1 0 ∗ x 2 2 ∗ x 3 0 =x_{0}^{1} * x_{1}^{0}*x_{2}^{2}*x_{3}^{0} =x01∗x10∗x22∗x30
- n_input_features_: 输入变量的个数
- n_output_features_: 输出变量的个数
from sklearn.preprocessing import PolynomialFeatures
from sklearn.datasets import load_iris
X,y=load_iris(return_X_y=True)
poly=PolynomialFeatures(degree=3,interaction_only=True,include_bias=False)
X_new=poly.fit_transform(X)
#自动生成新特征的名称
names=poly.get_feature_names(input_features=load_iris().feature_names)
3 处理计数
当数据大量且迅速地生成时,很有可能包含一些极端值。这时候就需要对数据进行检查,确定是应该保留数据原始的数值形式,还是将其转换成二值数据,或者进行粗粒度的分箱操作。
3.1 二值化
二值化的核心在于设定一个阈值,大于阈值的设为1,否则为0。
from sklearn.preprocessing import Binarizer
from sklearn.datasets import load_iris
X,y=load_iris(return_X_y=True)
#threshold参数用于设定阈值
bn=Binarizer(threshold=3)
X_new=bn.fit_transform(X)
3.2 区间分箱
区间分箱可以将连续变量离散化。在对变量进行区间量化之前,需要确定分箱宽度。有两种确定分箱宽度的方法:固定宽度分箱和分位数分箱。
区间分箱可以用pandas中的cut()(固定宽度分箱)和qcut(分位数分箱)方法实现,不再赘述。
4 Box-Cox变换
4.1 Box-Cox变换公式
Box-Cox变换主要用于用于连续的响应变量不满足正态分布的情况,其转化公式如下: x ′ = { x λ − 1 λ λ ≠ 0 l n ( x ) λ = 0 x^{'}=\begin{cases} \frac{x^{\lambda}-1}{\lambda}&\lambda \neq0 \\ ln(x) &\lambda =0 \end{cases} x′={λxλ−1ln(x)λ=0λ=0当 λ = 0 \lambda=0 λ=0时为对数变换;当 λ = 0.5 \lambda =0.5 λ=0.5时为平方根变换。当 λ \lambda λ小于1时,可以对大数值的范围进行压缩;当 λ \lambda λ大于1时,作用相反。以对数函数 f x ) = l o g 10 ( x ) fx)=log_{10}(x) fx)=log10(x)为例,当 x ∈ [ 1 , 10 ] x\in[1,10] x∈[1,10]时, f ( x ) ∈ [ 0 , 1 ] f(x)\in[0,1] f(x)∈[0,1]。当 x ∈ [ 10 , 100 ] x\in[10,100] x∈[10,100]时, f ( x ) ∈ [ 1 , 2 ] f(x)\in[1,2] f(x)∈[1,2]。注意,在对变量进行Box-Cox变换之前,要先对起进行归一化。
4.2 优点
Box-Cox变换的优点主要有以下几个方面:
- 通过求变换参数来确定变换形式的过程完全基于数据本身而无须任何先验信息,这无疑比凭经验或通过尝试而选用对数、平方根等变换方式要客观和精确。
- 对因变量 Y Y Y的数据变换可以明显地改善数据的正态性、对称性和方差齐性;对自变量X的数据变化可以改善模型结构,使得拟合的效果更好。
- Box-Cox变换可以让数据满足线性模型的基本假定,即线性、正态性及方差齐性(但经Box-Cox变换后数据是否同时满足了以上假定,仍需要考察验证)。
4.3 实现
import pandas as pd
from sklearn.linear_model import LinearRegression
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,mean_absolute_error
from scipy import stats
from matplotlib import pyplot as plt
from sklearn.preprocessing import FunctionTransformer
data=pd.read_csv('onlinenewspopularity.csv',usecols=[3,60])
#数据变换-对数变换
data_new=data.copy()
log_f=FunctionTransformer(np.log1p,validate=False)
data_new.iloc[:,0]=log.fit_transform(data_new.iloc[:,[0]])
#数据变换-BoxCox变换
data_new_2=data.copy()
data_new_2.iloc[:,0]+=1
data_new_2.iloc[:,0],lamb=stats.boxcox(data_new_2.iloc[:,0])
#分布散点图
fig=plt.figure(figsize=(10,20),dpi=80)
fig.add_subplot(3,1,1)
plt.scatter(data.iloc[:,0],data.iloc[:,1],label='normal')
plt.xlabel('Number of Words in Articles')
plt.ylabel('Number of Shares')
plt.legend()
fig.add_subplot(3,1,2)
plt.scatter(data_new.iloc[:,0],data.iloc[:,1],label='log transform')
plt.xlabel('log the Number of Words in Articles')
plt.ylabel('Number of Shares')
plt.legend()
fig.add_subplot(3,1,3)
plt.scatter(data_new_2.iloc[:,0],data.iloc[:,1],label='box-cox transform')
plt.xlabel('Box-Cox Number of Words in Articles')
plt.ylabel('Number of Shares')
plt.legend()
plt.show()
#模型训练
X_train,X_test,y_train,y_test=train_test_split(data.iloc[:,[0]],data.iloc[:,[1]],
test_size=0.2,random_state=0)
X_train_new=data_new.iloc[X_train.index,[0]]
X_test_new=data_new.iloc[X_test.index,[0]]
X_train_new_2=data_new_2.iloc[X_train.index,[0]]
X_test_new_2=data_new_2.iloc[X_test.index,[0]]
lr=LinearRegression()
lr.fit(X_train,y_train)
y_pred=lr.predict(X_test)
mae,mse=mean_absolute_error(y_test,y_pred),mean_squared_error(y_test,y_pred)
print("变换之前模型的准确率:MAE为{:.3f},MSE为{:.3f}".format(mae,mse))
lr1=LinearRegression()
lr1.fit(X_train_new,y_train)
y_pred1=lr1.predict(X_test_new)
mae,mse=mean_absolute_error(y_test,y_pred1),mean_squared_error(y_test,y_pred1)
print("对数变换之后模型的准确率:MAE为{:.3f},MSE为{:.3f}".format(mae,mse))
lr2=LinearRegression()
lr2.fit(X_train_new_2,y_train)
y_pred2=lr2.predict(X_test_new_2)
mae,mse=mean_absolute_error(y_test,y_pred2),mean_squared_error(y_test,y_pred2)
print("Box-Cox变换之后模型的准确率:MAE为{:.3f},MSE为{:.3f}".format(mae,mse))
(1)散点图
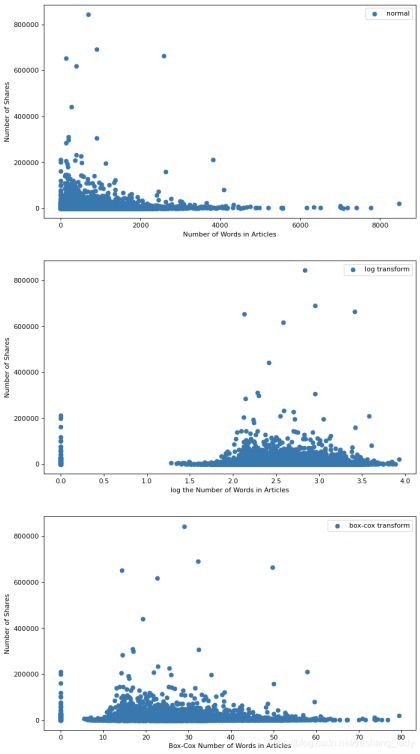
(2) 模型效果(在这里模型效果没有明显提升或降低)
变换之前模型的准确率:MAE为3174.127,MSE为76106487.136
对数变换之后模型的准确率:MAE为3172.253,MSE为76119780.290
Box-Cox变换之后模型的准确率:MAE为3176.513,MSE为76109830.747
5 类别型变量处理方法
前面介绍的特征处理方法大多用于数值型变量。还有一些特征处理方法仅适用于类别性变量。
5.1 One-Hot编码和哑变量编码
在以前的博文中已经介绍过这两种编码方法了,具体可以参考one-hot编码和哑变量编码,这里不再赘述。对类别型变量进行One-Hot编码或哑变量编码可以带来以下好处:
- 解决了分类器不好处理属性数据的问题。
- 将离散特征的取值扩展到了欧式空间,离散特征的某个取值就对应欧式空间的某个点。
- 使特征之间的距离计算更加合理。在回归,分类,聚类等机器学习算法中,特征之间距离的计算或相似度的计算是非常重要的,而我们常用的距离或相似度的计算都是在欧式空间的相似度计算,计算余弦相似性,基于的就是欧式空间。
- 在一定程度上也起到了扩充特征的作用。但当类别变量取值较多时,也需要配合特征选择来降低维度。
5.2 序号编码
如果类别型变量不同取值之间存在大小关系,则可以使用序号编码将类别型变量转换为数值。
import pandas as pd
data=pd.DataFrame(['二线','三线','二线','一线','超一线'],
columns=['城市发展等级'])
dev_map={'三线':1,'二线':2,'一线':3,'超一线':4}
data['dev_map']=data['城市发展等级'].map(dev_map)
tips: sklearn.preprocessing中提供了LabelEncoder类可以直接对特征进行序号编码,但该函数无法指定类别型变量的大小顺序,使用时要注意。
参考资料
- 《阿里云天池大赛赛题解析》
- 《特征工程》
- https://sangyx.com/1205
- https://www.cnblogs.com/whisper-yi/p/6079177.html