webGL第八课-绘制一个三维图形
之前看了二维绘图的知识,基本上了解了webGL的工作原理,下面开始了解一下三维的知识了
在看的过程中,会注意到之前没有留意的细节或知识,也一并进行记录和补充
视图矩阵
- 观察者所处的位置称为视点(eye point)。
- 从视点出发沿着观察方向的射线成为视线(viewing direction).
- 被观察目标所在的点,称作观察目标点(look-at point).
- 视点、观察目标点和上方向三个矢量,形成视图矩阵
webGL中,观察者默认状态为:
* 视点(0,0,0)
* 视线为Z轴负方向,观察点为(0,0,-1)
* 上方向为Y轴负方向,(0,1,0)
模型矩阵
用于对模型进行旋转、平移或缩放等基本变换矩阵称作模型矩阵(model matrix)
如果想实现这样的功能:对模型进行缩放旋转,然后从不同的角度对模型进行观察,则可以使用,视图矩阵X模型矩阵X原始坐标,来实现。
比如,我坐在办公桌前,看着面前的电脑,想换个角度看电脑。我可以先把电脑转个角度,然后我站起来,对电脑进行观察。把电脑转角度,使用模型矩阵控制;站起来使用视图矩阵控制。
这样,完全可以使用视图矩阵或者模型矩阵中的一个来进行调整,来达到同样的效果。如同书上说的:
“改变观察者状态”和“对整个世界进行平移和旋转变换”,本质上是一样的。
模型视图矩阵
为了方便,可以将视图矩阵X视图矩阵,结果作为一个矩阵传到webGL中,叫做模型视图矩阵。
投影矩阵
三角形独缺一角 —— 可视范围
例子中,出现三角形独缺一角问题,是因为没有指定可视范围,即实际观察得到的区域边界。可由投影矩阵操作来改善。
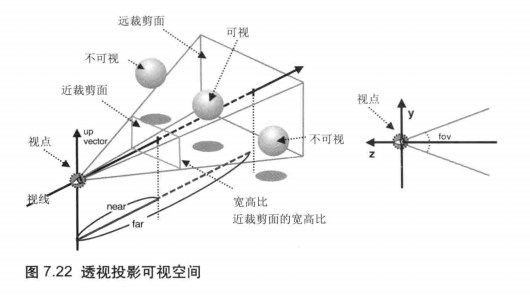
可视空间
水平视角、垂直视角和可视深度,定义了可视空间(view volume). 想想一下我们看东西的情况即可理解…
- 可视空间有两种常用:
- 长方形可视空间,由正射投影(orthographic projection)产生。
- 四棱锥/金字塔可视空间,由透视投影(perspective projection)产生。
正射投影
- 正射投影,即盒状可视空间,由近裁剪面(near clipping plane)和远裁剪面两个矩形表面构成。
上显示的就是可视空间中物体在近裁剪面上的投影。 如果可见面高宽比不同,会根据canvas高宽比对图像进行压缩处理。
使用正射投影矩阵设置正射投影效果
透视投影
定义了透视投影可视空间的矩阵成为透视投影矩阵
规范立方体(canonical view volume )
透视投影矩阵将金字塔形可视空间变换为盒状的可视空间,这个盒状可视空间又称规范立方体。
综上,投影矩阵、模型矩阵和视图矩阵相结合,就能够处理顶点需要经过的所有几何变换(平移、旋转、缩放),最终达到“具有深度感”的视觉效果。
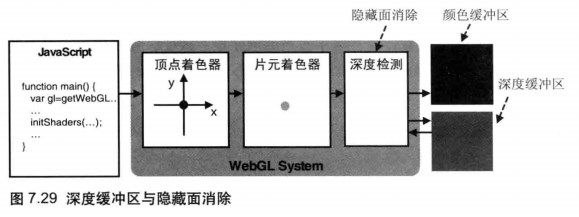
后面的图形遮挡前面的图形 —— 隐藏面消除
为了解决这个问题,webGL提供了隐藏面消除(hidden surface removal)功能。
- 开启隐藏面消除功能,需要遵循以下两步:*
- 开启隐藏面消除功能。 gl.enable(gl.depth_test);
- 在绘制之前,消除深度缓冲区。gl.clear(gl.depth_buffer_bit);
在绘制任意一帧之前,都必须清除深度缓冲区和颜色缓冲区
深度冲突 —— 多边形偏移机制(polygon offset)
- 启用多边形偏移机制:
- 启用多边形偏移。gl.enable(gl.polygon_offset_fill);
- 在绘制之前指定用来计算偏移量的参数。gl.polygonOffset(1.0,1.0);
绘制立方体 —— 引出光照
- 介绍了可以进行绘制的两个函数:gl.drawArrays() 和 gl.drawElements();
- 使用gl.drawelements()绘制渐变色和面单色立方体;
- 纯色无法显示出3D效果,需要使用光照技术。
列主序
webGL和openGL在存储矩阵时,按照列主序存储到数组中,所以如果要将一个矩阵存储到webGL中的矩阵对象中,需要将实际矩阵按照列主序进行存储。如图: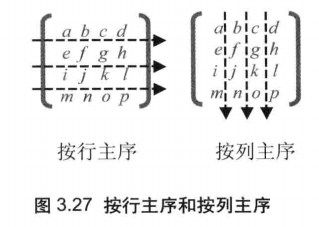
所以,定义一个数组时,应该这个顺序:
var newarr = new Float32Array([
a,e,i,m,b,f,j,n,c,g,k,o,d,h,l,p
])