【数字图像处理】实验(1)——图像基本变换
图像基本变换
- 一、实验意义及目的
- 二、实验内容
- 三、实验原理
- 四、Matlab相关函数介绍
- 五、代码及结果
-
- (1)将Image1色彩通道互换,并显示效果;
- (2)将Image1灰度化为gray,并显示灰度化后图像;
- (3)采用不同的插值方法实现gray的旋转、放大变换;
- (4)打开另一幅彩色图像Image2,和Image1进行代数运算,要求运用拼接、加减乘除等多种技术;
- (5)拓展内容
-
- (1)将彩色图像采用不同的灰度化方法实现灰度化;
- (2)将彩色图像变换到 YCbCr、HSV 空间,熟悉各分量数据并显示。
- (3)不采用 Matlab 函数,自行设计基于双线性插值的图像放大程序;
- 六、实验总结
一、实验意义及目的
(1)了解和掌握图像处理工具Matlab,熟悉基于Matlab的图像处理函数,并为下一步编程进行图像处理打下基础。
(2)理解色彩的概念,掌握图像代数运算,几何变换方法。
二、实验内容
1.打开一幅彩色图像Image1,使用Matlab图像处理函数,对其进行下列变换:
(1)将Image1色彩通道互换,并显示效果;
(2)将Image1灰度化为gray,并显示灰度化后图像;
(3)采用不同的插值方法实现gray的旋转、放大变换;
(4)打开另一幅彩色图像Image2,和Image1进行代数运算,要求运用拼接、加减乘除等多种技术;
(5)实验要求中的拓展内容。
2. 拓展内容:
(1)将彩色图像采用不同的灰度化方法实现灰度化;
(2)将彩色图像变换到 YCbCr、HSV 空间,熟悉各分量数据并显示;
(3)不采用 Matlab 函数,自行设计基于双线性插值的图像放大程序。
三、实验原理
1.灰度线性变换就是将图像中所有点的灰度按照线性灰度变换函数进行变换。
2.直方图均衡化通过点运算将输入图像转换为在每一级上都有相等像素点数的输出图像。
3.图像算术运算:两幅输入图像之间进行的点对点的加、减、乘、除运算后得到输出图像的过程。
4.图像插值是一种基本的图像处理方法,它可以为数字图像增加或减少像素的数目。
当图像被放大时,像素会相应地增加,该像素增加的过程实际就是插值程序自动选择信息较好的像素作为新的像素以弥补空白像素空间的过程。虽然经过插值后图像可以变得更平滑、干净,但由于新增加的像素也仅仅只是原始像素的某种组合而已,所以图像的插值运算并不会增加新的图像信息。
插值图像提供坐标–>计算该坐标在原始图像中的对应坐标–>原始图像返回像素值并进行插值运算双线性插值法充分利用了邻域像素的不同占比程度而计算得出最合适的插值像素,从而完成插值。相比较于最近邻插值,双线性插值的插值效果要好得多,因为最近邻插值只跟(x,y)最近的像素值有关,而双线性插值是按照(x,y)上下、左右四个像素值的重要程度进行插值的(即越接近越重要)。
四、Matlab相关函数介绍
(1)imread函数
功能:实现多种类型图像文件的读取,如:BMP、GIF、JPEG、PNG、RAS等。
调用格式:A = imread(filename, fmt)。filename为图像文件名,可以是灰度图像,也可以是彩色图像,如果文件不在当前目录或不在Matlab目录下,则需要列全文件路径。fmt为文件的扩展名,指定文件类型。A为图像数据矩阵。
(2)imshow函数
功能:显示图像。
调用格式:
imshow(I,n):显示灰度图像I,n为要显示图像的灰度等级,整数,默认为256。
Imshow(I,[LOW HIGH]):以规定的灰度级范围[LOW HIGH]来显示灰度图像I,低于LOW值的显示为黑,高于HIGH值的显示为白,默认按256个灰度级显示。
imshow(RGB):显示真彩色图像RGB。
imshow(BW):显示二值图像BW。
imshow(X,map):显示索引图像,X为索引图像的数据矩阵,map为其颜色映射表。
imshow filename:显示filename指定的图像,若文件包括多帧图像,则显示第一幅,且文件必须在MATLAB的当前目录下。
(3)imwrite函数
功能:实现图像文件的保存。
调用格式:
imwrite(A,’filename’,fmt):A是要保存的图像数据矩阵,filename是文件名,fmt是文件格式。
imwrite(X,map,’filename’,fmt):X为索引图像的数据矩阵,map为其颜色映射表。
(4)rgb2hsv函数
功能:实现RGB数据图像向HSV数据图像的转换。
调用格式:
HSV = rgb2hsv(RGB)。RGB为RGB彩色图像,为3维矩阵;HSV为3维HSV图像矩阵,3维依次为H、S、V,取值均在[0,1]范围内。
(5)rgb2ycbcr函数
YCBCR = rgb2ycbcr(RGB) :实现RGB数据图像向YCbCr数据图像的转换。
(6)rgb2gray函数
功能:彩色图像灰度化。
调用格式:
I = rgb2gray(RGB):真彩色RGB图像变换为灰度图像I。
NEWMAP = rgb2gray(MAP):变换索引图像的调色板为灰度调色板。
(7)imrotate函数
功能:实现图像旋转。
调用格式:
B = imrotate(A,ANGLE,METHOD,BBOX):A为要进行旋转的图像;ANGLE为要旋转的角度()逆时针为正,顺时针为负;METHOD为图像旋转插值方法,可取“‘nearest’, ‘bilinear’, ‘bicubic’”,默认为nearest;BBOX指定返回图像大小,可取“crop”,输出图像B与输入图像A具有相同的大小,对旋转图像进行剪切以满足要求;可取“loose”,默认是,B包含整个旋转后的图像。
(8)imresize函数
功能:实现图像缩放。
调用格式:
B = imresize(A, SCALE,METHOD)):返回原图A的SCALE倍大小图像B;
B = imresize(A, [NUMROWS NUMCOLS], METHOD)):对原图A进行比例缩放,返回图像B的行数NUMROWS和列数NUMCOLS,如果二者为NaN,表明Matlab自动调整了图像的缩放比例;
[Y, NEWMAP] = imresize(X, MAP, SCALE, METHOD)):对索引图像进行成比例缩放。
(9)imtransform函数
功能:实现图像几何变换。
调用格式:
B = imtransform(A,TFORM,INTERP,param1,val1,param2,val2,…) :对图像A实现空间变换,TFORM为maketform函数或cp2tform函数产生的结构;INTERP为插值方法,可取“‘nearest’, ‘bilinear’, ‘bicubic’”。
T = maketform(TRANSFORMTYPE,…):产生转换结构;TRANSFORMTYPE为变换类型,可以为“‘affine’, ‘projective’, ‘custom’, ‘box’, ‘composite’”。
(10)fliplr函数
B=fliplr(X):实现二维矩阵X沿垂直轴的左右翻转。
(11)flipud函数
B= flipud(X):实现二维矩阵X上下翻转。
(12)flipdim函数
B=flipdim(X,DIM):使矩阵X按特定轴翻转,dim指定翻转方式:为1表示按行翻转;为2表示按列翻转。
(13)permute函数
B = permute(A,ORDER):按照向量ORDER指定的顺序重排A的各维,B中元素和A中元素完全相同,但在A、B访问同一个元素使用的下标不一样。order中的元素必须各不相同。
(14)imadd函数
C=imadd(A,B) :实现两幅图像相加。
1)A、B均为图像,则要求B和A的尺寸相等;若B是一个标量,则C表示对图像A整体加上某个值(对小数部分取整)。
2)假如A和B对应运算和大于255,C仍取255,即截断处理;为避免截断,可以将C存储为uint16,即C=imadd(A,B,’uint16’)。
(15)imsubtract函数
功能:实现两幅图像相减。
调用格式:
C=imsubtract(A,B):差值结果小于0的赋值为0,对A、B的要求同imadd相同。
C=imabsdiff(A,B):差值结果取绝对值。
(16)immultiply 函数
C=immultiply(A,B):实现两幅图像相乘。
(17)imdivide函数
C=imdivide(A,B) :实现两幅图像相除。
五、代码及结果
(1)将Image1色彩通道互换,并显示效果;
代码:
Image1=imread('peppers.jpg');
%红绿通道互换
Image2=Image1;
Image2(:,:,1)=Image1(:,:,2);
Image2(:,:,2)=Image1(:,:,1);
imshow(Image2);
imwrite(Image2,'changecolor.jpg');
(2)将Image1灰度化为gray,并显示灰度化后图像;
代码:
Image1=imread('peppers.jpg');
%灰度化
gray=rgb2gray(Image1);
figure;
subplot(121),imshow(Image1),title('Original Image');
subplot(122),imshow(gray),title('Gray Image');
imwrite(gray,'grayimage.jpg');
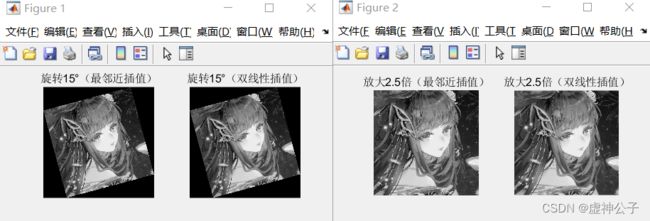
(3)采用不同的插值方法实现gray的旋转、放大变换;
代码:
Image1=imread('peppers.jpg');
%图像旋转
Newgray1=imrotate(gray,15);
Newgray2=imrotate(gray,15,'bilinear');
figure;
subplot(121),imshow(Newgray1),title('旋转15°(最邻近插值)');
subplot(122),imshow(Newgray2),title('旋转15°(双线性插值)');
imwrite(Newgray1,'rotate1.jpg');
imwrite(Newgray2,'rotate2.jpg');
%图像缩放
Newgray3=imresize(gray,2.5,'nearest');
Newgray4=imresize(gray,2.5,'bilinear');
figure;
subplot(121),imshow(Newgray3),title('放大2.5倍(最邻近插值)');
subplot(122),imshow(Newgray4),title('放大2.5倍(双线性插值)');
imwrite(Newgray3,'scale1.jpg');
imwrite(Newgray4,'scale2.jpg');
(4)打开另一幅彩色图像Image2,和Image1进行代数运算,要求运用拼接、加减乘除等多种技术;
代码:
Image1=imread('peppers.jpg');
%图像镜像与拼接
Image2=imread('lotus.bmp');
HImage=flipdim(Image2,2);
VImage=flipdim(Image2,1);
CImage=flipdim(HImage,1);
[h w]=size(Image2);
NewImage=zeros(h*2,w*2,3);
NewImage=[Image2 HImage;VImage CImage];
figure,imshow(NewImage);
imwrite(NewImage,'newlotus.jpg');
%图像的加减乘除
clc;
clear all;
ImageA = imread('lotus.bmp');
ImageB = imread('you.jpg');
%两张图之间要做运算首先需要有相同分辨率,将图片做了一个像素的统一化:
[a,b,c]=size(ImageA);
ImageB=imresize(ImageB,[a,b,]);
%分别对AB图像做了加 乘 除 减
Imagei = imadd(ImageA,ImageB);
Imagej = immultiply(ImageA, ImageB);
Imagek = imdivide(ImageA,ImageB);
Imagel = imsubtract(ImageA,ImageB);
figure;
subplot(321), imshow(ImageA);
subplot(322), imshow(Imagel);
subplot(323), imshow(ImageB);
subplot(324), imshow(Imagei);
subplot(325), imshow(Imagej);
subplot(326), imshow(Imagek);
结果:

两张图之间要做运算首先需要有相同分辨率,可以看到我们先将图片做了一个像素的统一化:
[注意这里的imresize,也可以用cat的方法(网络上有源代码),只要能把A图三个纬度的值分别赋给B的各个维度就可]
第一列的前两张为原图,做减法后的为第二列第一张;
最后一张几乎全白一张全黑的分别为图片相乘和除; 个人理解是由于乘法使得像素矩阵的值变大, 除法使得值变小, 众所周知值越大越趋向于全白,越小越趋向于全黑
(5)拓展内容
(1)将彩色图像采用不同的灰度化方法实现灰度化;
代码:
MyImage1 = imread('peppers.jpg');%读取彩色图像
%显示原来的图像
figure(1);
imshow(MyImage1);
%经过系统函数运算得到的灰度图像
MyGrayPic1 = rgb2gray(MyImage1);
figure(2);
imshow(MyGrayPic1);
[rows,cols,colors] = size(MyImage1);%得到原来图像矩阵的参数
MidGrayPic1 = zeros(rows,cols);%得到一个全0矩阵,用于存储之后生成的灰度图像
MidGrayPic1 = uint8(MidGrayPic1);%将创建的全0矩阵转换为uint8格式,因为用上面的语句创建之后图像是double型的
for i =1:rows
for j =1:cols
sum=0;
for k =1:colors
sum = sum+MyImage1(i,j,k)/3;%进行转化的关键公式,sum每次都因为后面的数字而不能超过255 ,
end
MidGrayPic1(i,j)=sum;
end
end
%平均值法转化后的灰度图像
figure(3);
imshow(MidGrayPic1);
MidGrayPic2=zeros(rows ,cols);%用得到的参数创建一个全0的矩阵,用于存储之后生成的灰度图像
MidGrayPic2=uint8(MidGrayPic2);%将创建的全0矩阵转换为uint8格式
for i=1:rows
for j=1:cols
MidGrayPic2(i,j)=max(MyImage1(i,j,:));
end
end
%最大值法转化之后的灰度图像
figure(4);
imshow(MidGrayPic2);
MidGrayPic3 = zeros(rows ,cols);%用得到的参数创建一个全0矩阵
MidGrayPic3 = uint8(MidGrayPic3);%将创建的全0矩阵转换为uint8格式
for i = 1:rows
for j=1:cols
MidGrayPic3(i , j) = MyImage1(i , j , 1)*0.30+MyImage1(i , j , 2)*0.59+MyImage1(i , j , 3)*0.11;
end
end
%加权平均值法转化之后的灰度图像
figure(5);
imshow(MidGrayPic3);
(2)将彩色图像变换到 YCbCr、HSV 空间,熟悉各分量数据并显示。
代码:
%将彩色图像变换到 YCbCr、HSV 空间,熟悉各分量数据并显示
Image = imread('peppers.jpg');
gray = rgb2gray(Image);
hsv = rgb2hsv(Image);
ycbcr = rgb2ycbcr(Image);
figure;
subplot(221);imshow(Image);title('原始图像');
subplot(222);imshow(gray);title('灰度图像');
subplot(223);imshow(hsv);title('HSV空间图像');
subplot(224);imshow(ycbcr);title('YCbCr图像');
%HSV空间显示其分量
figure;
H=hsv(:,:,1);
S=hsv(:,:,2);
V=hsv(:,:,3);
subplot(1,3,1);imshow(H);title('HSV空间H分量图像');
subplot(1,3,2);imshow(S);title('HSV空间S分量图像');
subplot(1,3,3);imshow(V);title('HSV空间V分量图像');
%YCbCr空间显示其分量
figure;
Y=ycbcr(:,:,1);
Cb=ycbcr(:,:,2);
Cr=ycbcr(:,:,3);
subplot(1,3,1); imshow(Y); title('YCbCr空间Y分量图像');
subplot(1,3,2); imshow(Cb); title('YCbCr空间Cb分量图像');
subplot(1,3,3); imshow(Cr); title('YCbCr空间Cr分量图像');
(3)不采用 Matlab 函数,自行设计基于双线性插值的图像放大程序;
代码:
% 相关基础知识;
% 图像插值是一种基本的图像处理方法,它可以为数字图像增加或减少像素的数目。
% 当图像被放大时,像素会相应地增加,该像素增加的过程实际就是插值程序自动
% 选择信息较好的像素作为新的像素以弥补空白像素空间的过程。虽然经过插值后
% 图像可以变得更平滑、干净,但由于新增加的像素也仅仅只是原始像素的某种组
% 合而已,所以图像的插值运算并不会增加新的图像信息。
% 插值图像提供坐标-->计算该坐标在原始图像中的对应坐标-->原始图像返回像素值并进行插值运算
% 双线性插值法充分利用了邻域像素的不同占比程度而计算得出最合适的插值像素,从而完成插值。
% 相比较于最近邻插值,双线性插值的插值效果要好得多,因为最近邻插值只跟(x,y)最近的像素值有关,
% 而双线性插值是按照(x,y)上下、左右四个像素值的重要程度进行插值的(即越接近越重要)
Image1 = imread('peppers.jpg'); % 读取RGB格式的图像
[rows,cols,colors] = size(Image1);
mutiple = 0.5;
newRows = round(rows * mutiple);
newCols = round(cols * mutiple);
scaleImage = uint8(zeros(newRows,newCols, colors));
% 给原图像加"墙壁"
ImageAddWalls = zeros(rows+2,cols+2,colors);
ImageAddWalls(1,2:cols+1,:) = Image1(1,:,:); % 源图像上面加墙,像素值和边界一致
ImageAddWalls(rows+2,2:cols+1,:) = Image1(rows,:,:);% 源图像下面加墙,像素值和边界一致
ImageAddWalls(2:rows+1,2:cols+1,:) = Image1; % 将原图像赋值给中心部分
ImageAddWalls(:,1,:) = ImageAddWalls(:,2,:); % 源图像左边加墙,像素值和边界一致
ImageAddWalls(:,cols+2,:) = ImageAddWalls(:,cols+1,:); % 源图像右边加墙,像素值和边界一致
for i = 1 : newRows
for j = 1 : newCols
originX = ( i + 0.5 ) * cols / newCols - 0.5;
orininY = ( j + 0.5 ) * rows / newRows - 0.5;
Q22_x = ceil(originX); % 找到Q22点的坐标
Q22_y = ceil(orininY);
if Q22_x == 1
Q22_x = 2;
end
if Q22_y ==1
Q22_y = 2;
end
Q11_x = Q22_x - 1;% 找到Q11点的坐标
Q11_y = Q22_y - 1;
Q21_x = Q22_x - 1;% 找到Q21点的坐标
Q21_y = Q22_y;
Q12_x = Q22_x;% 找到Q12点的坐标
Q12_y = Q22_y - 1;
% 根据公式,将公式处理成线性代数的矩阵运算,计算该点像素
derX = [Q22_x - originX , 1 - Q22_x + originX];
derY = [Q22_y - orininY ; 1 - Q22_y + orininY];
for k = 1:3
QPiexl = [ImageAddWalls(Q11_x,Q11_y,k), ImageAddWalls(Q21_x,Q21_y,k);ImageAddWalls(Q12_x,Q12_y,k),ImageAddWalls(Q22_x,Q22_y,k)];
scaleImage(i,j,k) = derX*QPiexl*derY;
end
end
end
figure,imshow(Image1),title('原图像');
figure,imshow(scaleImage),title('缩放后的图像');
imwrite(scaleImage,'scaleImg.jpg');
六、实验总结
图像插值四种模式
(1)Nearest (最近相邻插值算法/最近邻法)
1.最近相邻插值算法是一种速度快但精度低的图像像素模拟方法。
2.该法针对二维图像‘取待采样点周围4个相邻像素点距离最近的1个邻点的灰度值作为该点的灰度值’,该方法用于包含未消除锯齿边缘的插图,以保存硬边缘并生成较小的文件
3.缩放图片时,缺少的像素通过直接使用与之最接近的原有像素的颜色生成,也就是照搬旁边的像素,这样做的结果是产生明显可见的锯齿
(2)Bilinear(两次线性插值算法/双线性内插法)
1.两次线性插值算法是一种通过平均周围像素颜色来添加像素的方法,该方法可生成中等品质的图像。
2.两次线性插值算法‘输出的图像的每个像素都是原图中四个像素(2x2)运算的结果’,由于它是从原图四个像素中运算的,因此这种算法很大程度上消除了锯齿现象,而且效果也比较好。
(3)Bicubic(两次立方插值算法/立方卷积法)
1.两次立方插值算法是两次线性插值算法的改进,计算精度很高,处理后图像像质损失较小。
2.两次立方插值算法‘不仅考虑到四个直接邻点灰度值的影响,还考虑到各邻点间灰度值变化率的影响’,利用了待采样点周围更大邻域内像素的灰度值作三次插值。
3.两次立方插值算法‘不仅考虑到四个直接邻点灰度值的影响,还考虑到各邻点间灰度值变化率的影响’,利用了待采样点周围更大邻域内像素的灰度值作三次插值。
(4)Antialias(Lanczos算法)
1.Lanczos重采样通常用于提高数字信号的采样率,或将其偏移采样间隔的一小部分。它通常也用于多变量内插,例如用于调整大小或旋转一个数字图像。为此,已将其视为几个简单过滤器中的‘最佳折中方案’。
2.相对于其他插值算法,它应用于的邻域更广。
3.Antialias比Bicubic的速度要快,但Bicubic的更清晰些。