R计算两列数据的相关系数_数据相关性分析 correlation - R实现
相关性分析是指对两个或多个具备相关性的变量元素进行分析，从而衡量两个变量因素的相关密切程度。相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。
有时候多组数据需要分析其关联性（是否有正向/反向线性关联关系），这个时候就可以借助关联性分析了。如果只是两组线性数据比较，那只要比出来一个关联度就好了。但是如果是两个表格（多对多组数据，两两比较，就需要相关度表 correlation matrix了。
关联分析可以用pearson、spearman或者kendall三种关联分析方法，一般比较常用的是pearson，这个会考虑具体数值大小。在这里因为数据差异比较大，所以我选用了spearman方法来进行相关性分析。
关于相关性分析的三个算法区分可以参考这篇文章：相关性分析
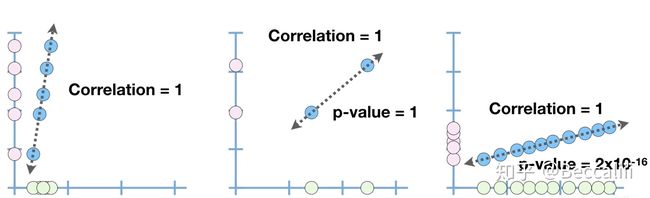
correlation的数值越接近1 或 -1，说明两组数据之间正向 或 反向 线性关联越强，但correlation总是要结合p-value一同考虑，才有意义。
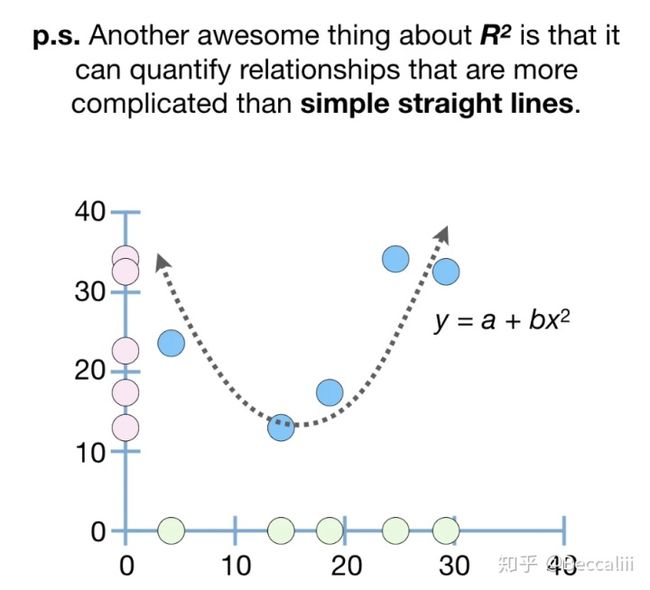
PS: 协方差corvariant 也是计算两组数据线性关系的，但由于协方差受data scale 影响很大，所以只看结果的符号来判断正向或反向关系。相关性correlation由corvariant计算得到，同时考虑了data scale，所以结果的数值大小和符号都可以作为参考，可以运用correlation和X来预测Y，但效果一般般。 所以，又引入了R2（R平方，R=pearson相关系数），一个能更好表达用X来预测Y的度量标准，同时还能用于非线性关系，R=0.9时，R2=0.81，说明81%的预测结果可以由Y/X关系来解析。此处不深入讲了。
以R来实现，
关于相关系数散点图（一对一） ，注意，如果数据是RNA reads counts，需要先转换成log(TPM) 再进行画图，因为1）基因reads数基于基因长度进行标准化是最基础的，否则无法进行比较； 2）log之后的数据画图会更好看，log不改变数据间关系。
a=log((rowMeans(tmp1))+1)
b=rowMeans(tmp2)
data=as.data.frame(cbind(a,b))
colnames(data)=c("valueA","valueB")
head(data)
library(ggplot2)
library(dplyr)
cor(a,b,method="pearson")
ggplot(data,aes(x=valueA,y=valueB))+ geom_point(size=1,shape=15)+geom_smooth(method=lm)
TPM、RPKM、CPM计算方法：https://zhuanlan.zhihu.com/p/150300801
关于相关系数矩阵（多对多），先读入矩阵数据，注意读入是numeric 类型
#install.packages("corrplot")
library(corrplot)
#matrix <- cor(data,method="spearman",use="everything")
matrix <- cor(data1,data2,method="spearman",use="complete.obs")
dim(matrix)
matrix[1:5,]
#correlation matrix
write.csv(matrix,file="data/spearman_correlation.csv",quote=F,row.names=T)
#correlation plot
png(file="corr_plot.png",width=3000,height=3000)
#数据少，半边的图
corrplot(matrix, type = "lower", order = "original", tl.col = "black", tl.srt = 45,cl.lim = c(0, 1))
#数据多，完整的图
#corrplot(matrix,title = "Correlation Plot",method = "color",outline = T, addgrid.col = "white", order="hclust", mar = c(0,0,1,0), addrect = 4, rect.col = "grey", rect.lwd = 1,cl.pos = "b", tl.col = "indianred4", tl.cex = 1, cl.cex = 3)
dev.off()这里png( , weight=, height= ) 的参数可以按需更改的。数据比较大的画数值设置大一点，出来的图片清晰度会大很多。因为屏幕大小有限，特征数多，图比较大的时候直接用jupyter notebook 或者rstudio看到的图片清晰度很低，所以一般打印出来看。
corrplot包的使用这一篇讲得很好，可以按需调整自己的代码：R语言绘制热图（其实是相关系数图）实践(二）corrplot包
其实correlation matrix就是数据两两比较，算出一个相关性数值，在根据数值的大小和正负方向来画热图，把数据可视化。
其实出了相关性结果数值，应该还有一个p-value的（即相关性结果数值随即得到的概率有多大），严谨一点的实验需要连同p-value一起考虑。接下来如果你想查看有多少是正相关，有多少是负相关的，可以用以下代码稍稍分析以下。
cor_JC<-as.numeric(matrix)
#如果是组内数据两两比较，会出现很多自己和自己比然后完全相关，结果=1的数值，记得移除（但不要移走其他1）
#cor_JC[1:5]
#rm=which(cor_JC==1) #remove cor 1
#cor_JC=cor_JC[-rm]
#cor_JC[1:5]
cor_JC[cor_JC >0.95]
sum(cor_JC >0.95)
cor_JC[cor_JC < -0.95]
sum(cor_JC < -0.95)按照相关性的说法,取 |0.95| 为阈值。
正相关：如果x,y变化的方向一致，如身高与体重的关系，r>0；一般地，
|r|>0.95 存在显著性相关；
|r|≥0.8 高度相关；
0.5≤|r|<0.8 中度相关；
0.3≤|r|<0.5 低度相关；
|r|<0.3 关系极弱，认为不相关
如果是一组数据，内部亮亮比对画图，则会看见对角线是一条全为1的线（自己跟自己比相关性）
另，如果需要参考特征值+年龄+性别等的影响，也可以用线性回归来做，y=a*age+b*gender+c*x+d,这样算出来会有一个R^2和p-value。可以用R^2来替代相关系数。
上文代码主要是用于作图，如果要查看生成关联度的具体数值分布并筛选出高关联度的几组数据，可以使用以下代码。（表内元素两两关联，不重复比对）
#INPUT DATA
metagenomics[1:2,]
#COORELATION
cor <- 0
d<-c("0","0","0")
end=dim(metagenomics)[2]-1
for (i in 1:end) {
x = metagenomics[,i]
s=i+1
for (j in s:dim(metagenomics)[2]) {
cor_n <- cor(x, y = metagenomics[,j], method = "pearson")
cor<-append(cor,cor_n)
if(as.numeric(as.character(cor_n))>0.9){
metab1<-colnames(metagenomics)[i]
metab2<-colnames(metagenomics)[j]
re<-c(metab1,metab2,cor_n)
d<-rbind(d,re)
}
}
}
d<-as.data.frame(d)
colnames(d)<-c("metab1","metab2","pearson_cor")
d<-d[-1,]
d[1:5,]
cor<-cor[-1]
summary(cor)
length(cor[cor >0.8])
length(cor[cor >0.9])
#frequency
hist(cor,breaks=100,xlim=c(-1,1))
abline(v = 0.9, col = "red")
置换检验 permutation test
置换检验（Permutation Test）www.bioinfo-scrounger.comPermutation test 置换检验是Fisher于20世纪30年代提出的一种基于大量计算（computationally intensive），利用样本数据的全（或随机）排列，进行统计推断的方法，因其对总体分布自由，应用较为广泛，特别适用于总体分布未知的小样本资料，以及某些难以用常规方法分析资料的假设检验问题。在具体使用上它和Bootstrap Methods类似，通过对样本进行顺序上的置换，重新计算统计检验量，构造经验分布，然后在此基础上求出P-value进行推断。
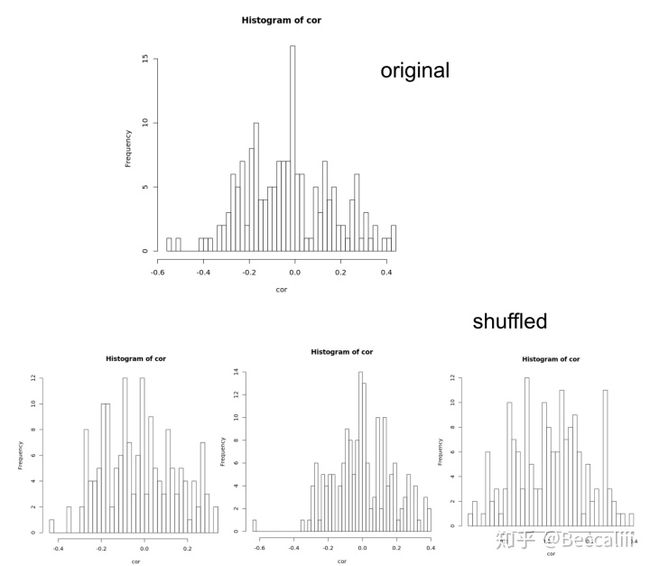
简单来说，就是假设x1和x2两列数据求相关性（正常来说x1和x2的样本ID顺序需要一致），那我们如何知道，按这个顺序求出来的相关性是偶然间得到的，还是数据特别但却得到了这个结果呢？就要做置换检验。打乱其中一组的顺序，看得到的相关系数的范围是否与原来结果相近，如果相近，则证明随便乱来的数据计算结果也能与真实数据的结果相近，x1和x2的相关性比较无意义。
data<-as.data.frame(read.table("data/metabolomics_metagenomics_34JC.csv",sep=",",header=T,row.names=1,stringsAsFactors=F))
data<-t(data[-c(1,2),])
metagenomics<-data[,1:169]
metabolites<-data[,170:295]
#shuffles label in one group
j = sample(1:nrow(metabolites),1*nrow(metabolites))
#metabolites = metabolites[j,]
#metagenomics = metagenomics[j,]
#metagenomics[1:2,]
#metabolites[1:2,]
cor <- numeric(dim(metagenomics)[2])
for (i in 1:dim(metagenomics)[2]) {
cor[i] <- cor(x = metabolites[,1], y = metagenomics[,i], use = "everything", method = "spearman")
}
#med
hist(cor,breaks=100)
#inter <- quantile(med, c(0.025,0.975))
#inter
如果置换检验（多试几次）得到原来结果和随机结果的覆盖范围不一致，则不重叠的部分数据有意义，可以继续进行分析。