基于MATLAB语音信号的处理与滤波
摘要:MATLAB是十分强大的用于数据分析和处理的工程实用软件,利用其来进行语音信号的分析、处理和可视化十分便捷。文中介绍了在MATLAB环境中如何驱动声卡采集语音信号和语音信号采集后的文档处理方法,并介绍了FFT频谱分析原理及其显示、MATLAB中相关函数的功能、滤波器的设计和使用。在此基础上,对实际采集的一段含噪声语音信号进行了相关分析处理,包括对语音信号的录取和导入,信号时域和频域方面的分析,添加噪声前后的差异对比,滤波分析,语音特效处理。结果表明利用MATLAB处理语音信号十分简单、方便且易于实现。
关键词:语音信号; MATLAB; 数字滤波; 滤波器;
一、设计内容:
语音信号处理技术的发展体现在生活中的各个方面,其重要性和现实意义也早已超乎大众的想象,早期的BB机到 电话、大哥大到手机和智能机的这一系列发展表明语音信号 处理技术正迅速发展。目前,在语音信号处理方面已经取得 了非常大的进展,语音信号处理技术在计算机接口与人机交 互方面应用得最为广泛。语音信号处理技术涵盖得非常广泛,包括语音识别、说话人的识别和确定、语种的识别和确认、关键词的检测和确认、语音的合成和语音编码等。目前,最富前景和挑战性的就是语音识别的技术,该技术在现实生活中已经有了具体的实际应用,其在车载导航、视频监控、网络视 讯等人机交互领域有着非常广泛的应用。而其中高性能的 连续语音、大词汇量语音识别系统是当前语音识别技术的前沿代表;同时语音信号的准确性识别也是亟待解决的主要任务。本文选用语音处理技术作为研究项目,是一次非同寻常的尝试。另外,采用 MATLAB来进行一系列的研究处理。MATLAB是一个功能强大的计算软件,在 MATLAB中 可以非常方便、快捷地处理很多技术。此次在MATLAB中完成相关滤波器的设计,因为 MATLAB在参数调整上非常简便快捷,这在很大程度上减轻了研究者的工作量,对滤波器的优化也非常有利。下列是本次项目的任务:
1.熟悉并掌握MATLAB中有关声音(wave)录制、播放、存储和读取的函数。
2.在MATLAB环境中,使用声音相关函数录制2秒左右自己的声音,抽样率是8000Hz/s,以及如何排除对这些无效点的采样。
3.分别取8000个和16000个数据进行频谱分析,得到幅度和相位谱,比较二者异同并分析原因,利用窗函数和双线性变换法设计。
4.针对电话信道(最高3500Hz),设计一个FIR或IIR滤波器进行滤波,把抽样率转变为7000Hz/s,并进行频谱分析,得到幅度和相位谱。
5.对声音进行背景噪声滤除,把处理后的所有数据储存为声音文件,与原始声音进行比较。
二、设计原理
1.语音信号的采集
为了将原始的模拟语音信号转变为数字信号,必须进行采样和量化,进而得到时间和幅度上均为离散的数字语音信号。又因为 MATLAB只能处理“.wav”结尾的音频信号,所以在录制声音的时候,格式不匹配就需要利用格式工厂软件进行格式转化。而且通过程序[x,fs,bits]=wavread(‘bishe.wav’)来读取语音信号时,MATLAB默认的fs=44100Hz,故调整频率为8000Hz。
2.语音信号的频谱分析
首先画出语音信号的时域波形,然后对语音号进行快速傅里叶变换,得到信号的频谱特性,从而加深对频谱特性的理解。
3.设计数字滤波器并得出其频率响应
各滤波器的性能指标:
(1)低通滤波器性能指标:fb=1000 Hz,fc=1200 Hz,As=100dB,Ap=1dB。
(2)高通滤波器性能指标:fc=4800 Hz,fb=5000 Hz As=100dB,Ap=1dB。
(3)带通滤波器性能指标:fp1=1200 Hz,fp2=3000 Hz,fsc1=1000 Hz,fsc2=3200Hz,As=100dB,Ap=1dB。
用窗函数法和双线性变换法设计上面要求的3种滤波器。在Matlab中,使用函数butter,cheby1等函数设计IIR滤波器;利用Matlab中的函数freqz得出各滤波器的频率响应。
4.用滤波器对信号进行滤波
用自己设计的各种滤波器分别对采集的信号进行滤波,在Matlab中,FIR滤波器利用函数fftfilt对信号进行滤波,IIR滤波器利用函数filter对信号进行滤波。在将语音信号进行数字化前,必须先进行防混叠预滤波,预滤波的目的有两个,一是抑制输入信导各领域分量中频率超出1/2的所有分量(为采样频率),以防止混叠干扰;二是抑制50Hz的电源工频干扰。预滤波器必须是一个带通滤波器,设其上、下截止颜率分别是和。
5.比较滤波前后语音信号的波形及频谱
然后在一个窗口同时画出滤波前后的波形及频谱。
6.回放语音信号
在Matlab中,使用相关声音函数对声音进行回放。辨别滤波前后的声音有何变化。优先构造回声的模型,以前输入的延迟和当前输入的叠加得到输出,而回声的明显程度就和Delay有关系
7. 背景噪声滤除
再录制一段同样长时间的背景噪声(频谱能量集中在某个小范围内)叠加到你的语音信号中,分析叠加前后信号频谱的变化,设计一个合适的滤波器,能够把该噪声滤除。
三、设计过程
1.语音信号采集
fs = 8000; % 采样频率
duration = 2; % 时间长度(秒)
n = duration*fs; % 采样点数
t = (1:n)/fs;
%创建一个录音文件:fs =8000
recObject = audiorecorder(fs, 16, 1);
fprintf('开始录音:\n');pause(0);
recordblocking(recObject, duration);
stop(recObject);
fprintf('录制结束\n');
play(recObject); % 播放录制的音频
y = getaudiodata(recObject);
ymax = max(abs(y)); % 归一化
y = y/ymax;
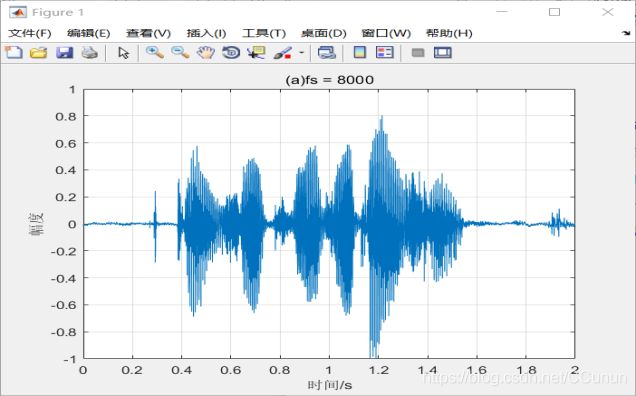
2.绘制波形图,见图1
audiowrite('audio1.wav', y, fs); % 写入音频
figure(1);
plot(t, y);
xlabel('时间/s');
ylabel('幅度');
title('(a)fs = 8000');
Grid;图1.原声 波形图
通过观察图形,发现在录音过程中出现了这样一个现象:录制刚开始时,出现一些无效的点,后面也出现一些无效的点。出现这种现象的原因主要是录音开始时,人的反应相对电脑开始录制慢了,导致出现了一些无效点,而后面出现的无效的点,主要是已经没有声音的动作。所以解决无效点出现,只需要将有效点位置单独截取出来然后重新绘制时域图形就能解决。
- 分别取8000个与16000个数据进行频谱分析
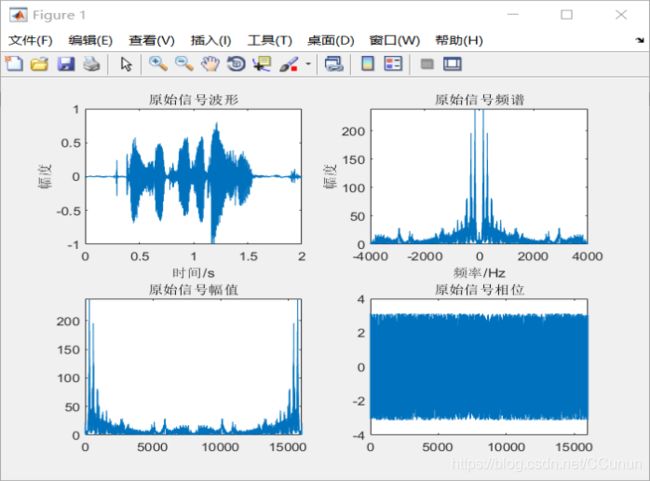
先对语音信号预处理结果及分析,如图2所示。
图2 语音信号预处理结果分析
对采集到的语音信号分别做傅里叶变换进行频谱分析,并显示频谱图,观察各自的幅频谱特性。该频谱图横坐标并未进行对应关系处理,但仍不失其频谱特性的本质,由频谱图可清楚地看到样本声音主要以低频为主。人的语音信号频率一般集中在1kHz之前,从声音频谱的包络来看, 根据采样定理,信号宽度近似取为1kHz,重放语音后仍可较清晰的听出原声, 不存在声音混叠现象。
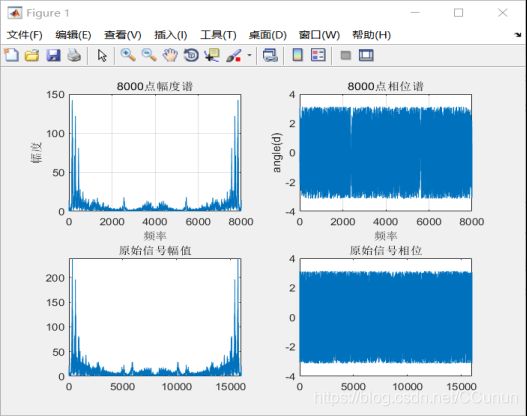
对8000个数据进行分析,如图3所示。
y=audioread('C:\Users\Lenovo\Desktop\audio project\audio1.wav');
d=fft(y,8000); %对语音信号8000点进行FFT变换
subplot(2,2,1);
plot(abs(d));
xlabel('频率');
ylabel('幅度');
title('8000点幅度谱');
grid;
subplot(2,2,2);
plot(angle(d));
xlabel('频率');
ylabel('angle(d)');
title('8000点相位谱');
grid;图3.8000点的FFT变换
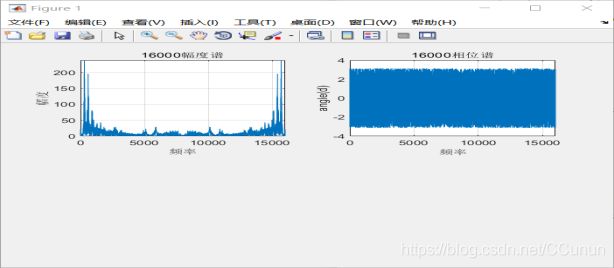
对16000个数据进行分析,如图4所示。
y=audioread('C:\Users\Lenovo\Desktop\audio project\audio1.wav');
d=fft(y,16000); %对语音信号进行FFT变换
subplot(2,2,1);
plot(abs(d));
xlabel('频率');
ylabel('幅度');
title('16000幅度谱');
grid;
subplot(2,2,2);
plot(angle(d));
xlabel('频率');
ylabel('angle(d)');
title('16000相位谱');
grid;图4 16000点的FFT变换
由图4可得8000点和16000点的幅度谱和相位谱基本相同,但8000比16000的图形线有点稀疏,故,点数越多,线条越密集。
- 针对电话信道(最高3500Hz),设计一个FIR或IIR滤波器进行滤波,把抽样率转变为7000Hz/s,并进行频谱分析,得到幅度和相位谱。
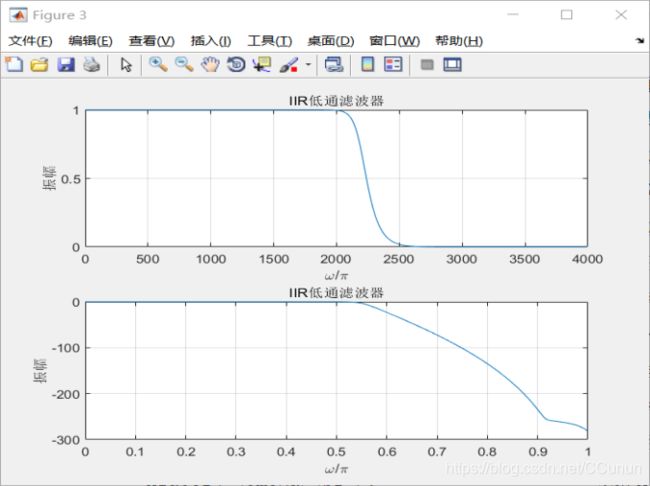
设计一个针对电话信道的IIR型低通滤波器,如图5所示。
%利用buttord设计IIR低通滤波器
rp=0.5;rs=60; %通带波纹系数rp,最小阻带衰减rs
Ft=7000;
Fp=1200;
Fs=2000;
wp=2*pi*Fp/Ft;
ws=2*pi*Fs/Ft; %求出待设计的模拟滤波器的边界频率
[n,wn]=buttord(wp,ws,rp,rs,'s') %低通滤波器的阶数和截止频率
[b,a]=butter(n,wn,'s'); %滤波器的传输函数
[bz,az]=bilinear(b,a,0.5);
%利用双线性变换实现频率响应S域到Z域的变换
%低通滤波器特性
figure(3);
[h,w]=freqz(bz,az); %利用freqz函数求频率响应
subplot(2,1,1);
plot(w*fs/(2*pi),abs(h)); %二维连续图形
grid;
title('IIR低通滤波器');
xlabel('\omega/\pi');
ylabel('振幅');
subplot(2,1,2);
plot(w/pi,20*log10(abs(h)));
grid;
title('IIR低通滤波器');
xlabel('\omega/\pi');
ylabel('振幅');图5 IIR低通滤波器的幅频特性
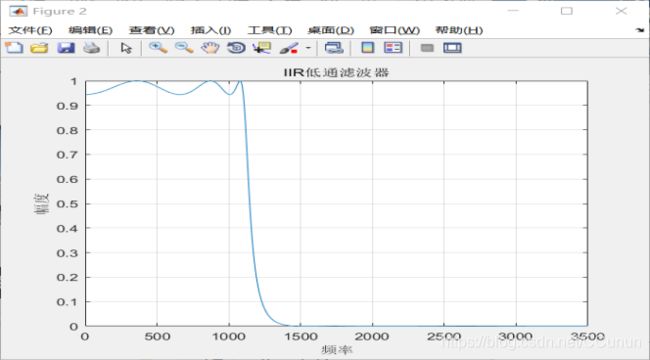
%利用ellipord设计IIR低通滤波器,如图6所示。
Fp=1200;
Fs=2000;
Ft=7000;
As=60;
Ap=0.5;
wp=2*pi*Fp/Ft;
ws=2*pi*Fs/Ft;
[n,wn]=ellipord(wp,ws,Ap,As,'s');
[b,a]=ellip(n,Ap,As,wn,'s');
[B,A]=bilinear(b,a,1);
[h,w]=freqz(B,A); %利用freqz函数求频率响应
figure(2);
plot(w*Ft/pi/2,abs(h));
title('IIR低通滤波器');
xlabel('频率');
ylabel('幅度');
grid;图6 利用ellipord设计IIR低通滤波器的幅频特性
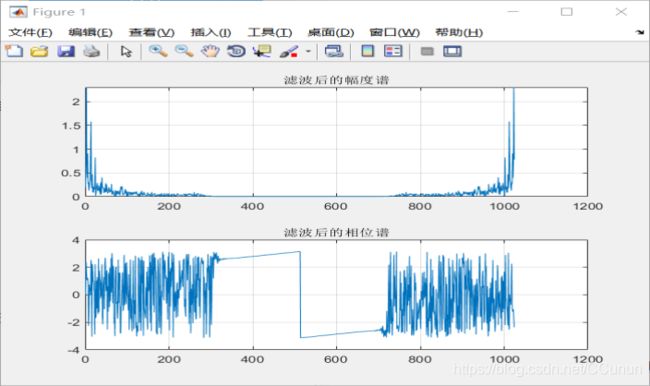
5.对录制的声音进行滤波处理,如图7所示。
fs=8000;
y=audioread('C:\Users\Lenovo\Desktop\audio project\audio1.wav');
f=filter(bz,az,y); %滤波
f1=fft(f,1024);
subplot(2,1,1)
plot(abs(f1)); %滤波后的时域图
title('滤波后的幅度谱');
grid;
subplot(2,1,2)
plot(angle(f1)); %滤波后的时域图
title('滤波后的相位谱');
grid;
audiowriter('C:\Users\Lenovo\Desktop\audio project\audio2.wav',f,fs);
%对滤波后的声音进行储存。图7 对录制的声音进行滤波处理
声音滤波完成,进行下一步。
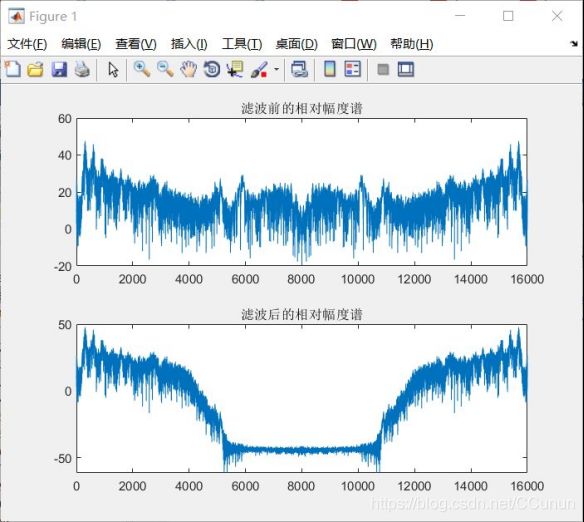
6.将处理后的声音与原声音进行对比,如图8所示。
fs=8000;
y=audioread('C:\Users\Lenovo\Desktop\audio project\audio1.wav');
y1=audioread('C:\Users\Lenovo\Desktop\audio project\audio2.wav');
yx=fft(y);
yx1=fft(y1);
subplot(2,1,1)
plot(20*log10(abs(yx)));
title('滤波前的相对幅度谱');
subplot(2,1,2);
plot(20*log10(abs(yx1)));
title('滤波后的相对幅度谱');图8 滤波前后的相对幅度谱
通过滤波前后两种信号的对比,它们的幅度基本一致,但原声比滤波后的声音清晰和自然,因原声经过低通滤波器后,其将信号高频部分滤掉,只余低频。
7.回放语音信号
clear
clc
[audio1,fs]=audioread('audio1.wav');
sound(audio1,fs);
Pause;
[audio2,fs]=audioread('audio2.wav');
sound(audio2,fs);声音变化:原声倾向于自然清晰,滤波后的声音则偏向低沉和忧郁。
通过sound函数重放滤波后的语音可以发现,噪声已经比较微弱,可以清晰地 听到“XX科技大学”这几个字。
四、结论
MATLAB提供了许多专用工具箱,灵活利用这些工具箱和函数,可以实现很多信号处理任务。同时,MATLAB还支持用户对其函数进行二次开发,以满足不同要求。在信号处理过程中,MATLAB兼顾了专用工具软件的简单性和计算机程序语言的灵活性,特别是处理效果的可视性和可感知,有利于理解信号处理的本质,有利于激发学习和研究兴趣,也有利于培养MATLAB软件的操作技能。
本文首先利用MATLAB完成语音的录制、读取,设置适当的采样频率对信号进行采样,并绘制出原始语音信号在时间域上的波形,利用快速傅里叶变换得到语音信号在频率域上的波形图;其次,对采集的语音信号进行加噪处理,绘制出添加噪声之后的语音信号的时域波形和频域波形图;
最后,通过设计滤波器来对加噪后的语音信号进行滤波,对比其滤波前后的波形变化。在整个研究过程中,MATLAB软件用于实现声音的回放、时域上的波形和频域上的波形显示。采样时需要设置合适的采样频率来满足采样定理,以便能恢复原始音频;再通过设置合理的性能参数,利用窗函数法和双 线性变换法的设计方法,完成IIR数字滤波器的设计。