【ACM】hud1166 敌兵布阵（线段树）

经验： cout 特别慢 如果要求速度 全部用 printf !!!

 

在学习线段树

内容来自：http://www.cnblogs.com/shuaiwhu/archive/2012/04/22/2464583.html 作者Microgoogle

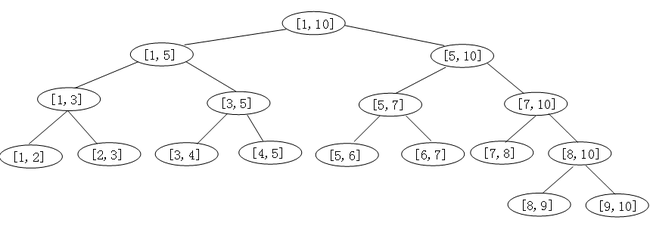
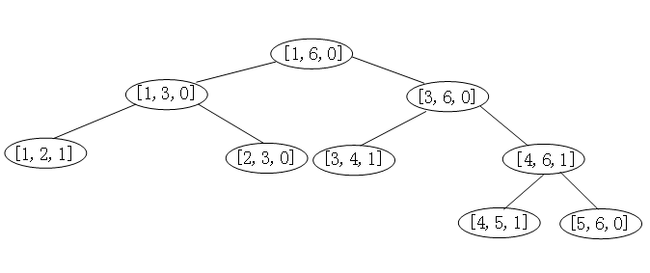
线段树在一些acm题目中经常见到，这种数据结构主要应用在计算几何和地理信息系统中。下图就为一个线段树：

(PS：可能你见过线段树的不同表示方式，但是都大同小异，根据自己的需要来建就行。)

1.线段树基本性质和操作

线段树是一棵二叉树，记为T(a, b)，参数a,b表示区间[a,b]，其中b-a称为区间的长度，记为L。

线段树T(a,b)也可递归定义为：

若L>1 :  [a, (a+b) div 2]为 T的左儿子；

             [(a+b) div 2,b]为T 的右儿子。 

若L=1 : T为叶子节点。

 

线段树中的结点一般采取如下数据结构：

struct Node
{
    int   left,right;  //区间左右值
    Node   *leftchild;
    Node   *rightchild;    
};

线段树的建立：

Node   *build(int   l ,  int r ) //建立二叉树
{
    Node   *root = new Node;
    root->left = l;
    root->right = r;     //设置结点区间
    root->leftchild = NULL;
    root->rightchild = NULL;

    if ( l +1< r )
    {
       int  mid = (r+l) >>1;
       root->leftchild = build ( l , mid ) ;
       root->rightchild = build ( mid  , r) ; 
    } 

    return    root; 
}

线段树中的线段插入和删除：

增加一个cover的域来计算一条线段被覆盖的次数，因此在建立二叉树的时候应顺便把cover置0。

插入一条线段[c,d]：

void  Insert(int  c, int d , Node  *root )
{
       if(c<= root->left&&d>= root->right) 
           root-> cover++;
       else 
       {
           if(c < (root->left+ root->right)/2 ) Insert (c,d, root->leftchild  );
           if(d > (root->left+ root->right)/2 ) Insert (c,d, root->rightchild  );
       }
} 

 

删除一条线段[c,d]:

void  Delete (int c , int  d , Node  *root )
{
       if(c<= root->left&&d>= root->right) 
           root-> cover= root-> cover-1;
       else 
       {
          if(c < (root->left+ root->right)/2 ) Delete ( c,d, root->leftchild  );
          if(d > (root->left+ root->right)/2 ) Delete ( c,d, root->rightchild );
       }
} 

2.线段树的运用

线段树的每个节点上往往都增加了一些其他的域。在这些域中保存了某种动态维护的信息，视不同情况而定。这些域使得线段树具有极大的灵活性，可以适应不同的需求。

例一：

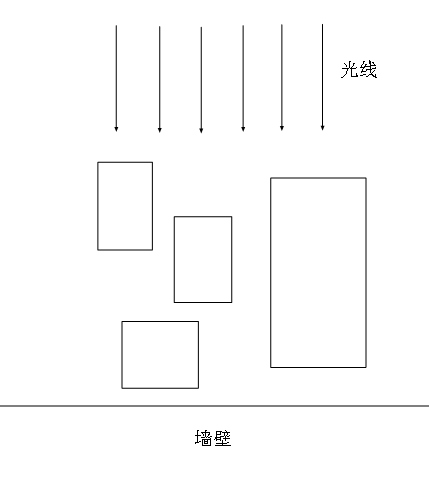
桌子上零散地放着若干个盒子，桌子的后方是一堵墙。如图所示。现在从桌子的前方射来一束平行光， 把盒子的影子投射到了墙上。问影子的总宽度是多少？

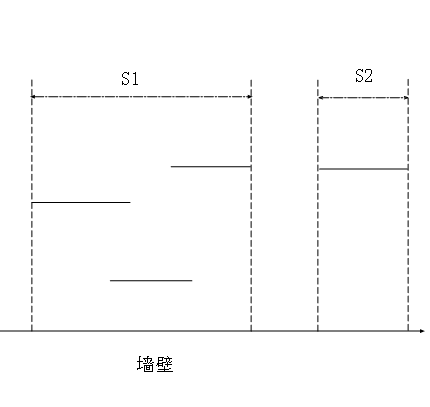
这道题目是一个经典的模型。在这里，我们略去某些处理的步骤，直接分析重点问题，可以把题目抽象地描述如下：x轴上有若干条线段，求线段覆盖的总长度，即S1+S2的长度。

 

2.1最直接的做法：

设线段坐标范围为[min,max]。使用一个下标范围为[min,max-1]的一维数组，其中数组的第i个元素表示[i,i+1]的区间。数组元素初始化全部为0。对于每一条区间为[a,b]的线段，将[a,b]内所有对应的数组元素均设为1。最后统计数组中1的个数即可。

初始     0   0  0  0  0
[1，2]   1   0  0  0  0
[3，5]   1   0  1  1  0
[4，6]   1   0  1  1  1
[5，6]   1   0  1  1  1

其缺点是时间复杂度决定于下标范围的平方，当下标范围很大时（[0,10000]），此方法效率太低。

2.2离散化的做法：

基本思想：先把所有端点坐标从小到大排序，将坐标值与其序号一一对应。这样便可以将原先的坐标值转化为序号后，对其应用前一种算法，再将最后结果转化回来得解。该方法对于线段数相对较少的情况有效。

示例:

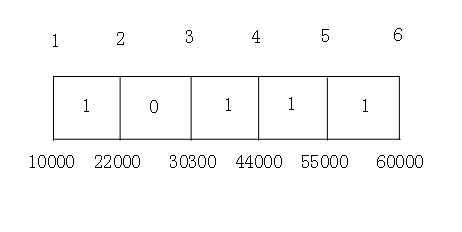
[10000,22000]   [30300,55000]   [44000,60000]   [55000,60000]

排序得10000，22000，30300，44000，55000，60000

对应得1， 2， 3， 4， 5， 6

然后是 [1,2]     [3,5]    [4,6]    [5,6]

初始     0   0  0  0  0
[1，2]   1   0  0  0  0
[3，5]   1   0  1  1  0
[4，6]   1   0  1  1  1
[5，6]   1   0  1  1  1

10000，22000，30300，44000，55000，60000

1，       2，        3，       4，       5，       6

(22000-10000)+(60000-30300)=41700

 

此方法的时间复杂度决定于线段数的平方，对于线段数较多的情况此方法效率太低。

2.3使用线段树的做法：

给线段树每个节点增加一个域cover。cover=1表示该结点所对应的区间被完全覆盖，cover=0表示该结点所对应的区间未被完全覆盖。

如下图的线段树，添加线段[1,2][3,5][4,6]

插入算法：

void   Insert(Node  *root , int  a , int  b)
{
    int m;
    if( root ->cover == 0) 
    { 
        
        m = (root->left+ root->right)/2 ;
        if (a == root->left && b == root->right) 
            root ->cover =1;
        else if (b <= m)  Insert(root->leftchild , a, b);
        else if (a >= m)  Insert(root->rightchild , a, b);
        else 
        {    
                Insert(root->leftchild ,a, m);
                Insert(root->rightchild , m, b);
        }
    }
}

统计算法：

int  Count(Node *root)
{
    int  m,n;
    if (root->cover == 1)
            return   (root-> right - root-> left);
    else if (root-> right - root-> left== 1 )return 0;
    m= Count(root->leftchild);
     n= Count(root->rightchild);
    return m+n;
}

 

 

-----------------------------------------------------------------------------------------------

题目：

Problem Description

C国的死对头A国这段时间正在进行军事演习，所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段，所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动，可能增加或减少若干人手,但这些都逃不过C国的监视。
中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动，而Derek每次询问的段都不一样，所以Tidy不得不每次都一个一个营地的去数，很快就精疲力尽了，Derek对Tidy的计算速度越来越不满:"你个死肥仔，算得这么慢，我炒你鱿鱼!”Tidy想：“你自己来算算看，这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下，Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说：“死肥仔，叫你平时做多点acm题和看多点算法书，现在尝到苦果了吧!”Tidy说："我知错了。。。"但Windbreaker已经挂掉电话了。Tidy很苦恼，这么算他真的会崩溃的，聪明的读者，你能写个程序帮他完成这项工作吗？不过如果你的程序效率不够高的话，Tidy还是会受到Derek的责骂的.

 

Input

第一行一个整数T，表示有T组数据。
每组数据第一行一个正整数N（N<=50000）,表示敌人有N个工兵营地，接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人（1<=ai<=50）。
接下来每行有一条命令，命令有4种形式：
(1) Add i j,i和j为正整数,表示第i个营地增加j个人（j不超过30）
(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人（j不超过30）;
(3)Query i j ,i和j为正整数,i<=j，表示询问第i到第j个营地的总人数;
(4)End 表示结束，这条命令在每组数据最后出现;
每组数据最多有40000条命令

 

Output

对第i组数据,首先输出“Case i:”和回车,
对于每个Query询问，输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。

 

Sample Input

1

10

1 2 3 4 5 6 7 8 9 10

Query 1 3

Add 3 6

Query 2 7

Sub 10 2

Add 6 3

Query 3 10

End

 

Sample Output

Case 1:

6

33

59

 

我自己写的代码：

#include <iostream>
#include <string>
using namespace std;


typedef struct Node
{
    int left, right; //区间左右值
    int peopleNum; //区间总人数
    Node *pLeft, *pRight; //子区间指针
}Node;

Node * build(int l, int r) //建立线段树
{
    Node * root = new Node;
    root->left = l;
    root->right = r;
    root->pLeft = NULL;
    root->pRight = NULL;
    root->peopleNum = 0;

    if(l < r)
    {
        int mid = (r + l) >> 1;
        root->pLeft = build(l, mid);
        root->pRight = build(mid + 1, r);
    }
    if(l == r)
    {
        cin >> root->peopleNum;
    }
    return root;
}

int updateTree(Node * root)
{
    int leftPartNum = 0;
    int rightPartNum = 0;
    if(root->pLeft != NULL)
    {
        leftPartNum = updateTree(root->pLeft); 
    }
    if(root->pRight != NULL)
    {
        rightPartNum = updateTree(root->pRight);
    }
    root->peopleNum += leftPartNum + rightPartNum;
    return root->peopleNum;
}

void updateAdd(Node * root, int group, int num)
{
    int m = (root->left + root->right) >> 1;
    root->peopleNum += num;
    if(root->left == root->right)
    {
        return;
    }
    else if(group >= m + 1)
    {
        updateAdd(root->pRight, group, num);
    }
    else
    {
        updateAdd(root->pLeft, group, num);
    }
}

void updateSub(Node * root, int group, int num)
{
    int m = (root->left + root->right) >> 1;
    root->peopleNum -= num;
    if(root->left == root->right)
    {
        return;
    }
    else if(group >= m + 1)
    {
        updateSub(root->pRight, group, num);
    }
    else
    {
        updateSub(root->pLeft, group, num);
    }
}

int getRangeNum(Node * root, int data1, int data2)
{
    int num = 0;
    if(root == NULL)
    {
        return 0;
    }
    int m = (root->left + root->right) >> 1;
    if(data1 == root->left && data2 == root->right) //区间恰好重合
    {
        num = root->peopleNum;
    }
    else if(data1 >= m + 1) //都在右子树
    {
        num += getRangeNum(root->pRight, data1, data2);
    }
    else if(data2 <= m) //都在左子树
    {
        num += getRangeNum(root->pLeft, data1, data2);
    }
    else
    {
        num += getRangeNum(root->pLeft, data1, m);
        num += getRangeNum(root->pRight, m + 1, data2);
    }
    return num;
}

int main()
{
    string Cmd;
    int N = 0; //总数据组数
    cin >> N;

    for(int i = 1; i <= N; i++)
    {
        //建立线段树
        int groupNum = 0;
        Node * root = NULL;
        Cmd = "";

        cin >> groupNum;
        root = build(1, groupNum);
        updateTree(root);

        cout << "Case " << i << ":"<< endl;

        //处理查询、增减
        while(Cmd != "End")
        {
            int data1, data2;
            cin >> Cmd;
            if(Cmd != "End")
            {
                 cin >> data1 >> data2;
            }
            if(Cmd == "Query")
            {
                cout << getRangeNum(root, data1, data2) << endl;
            }
            else if(Cmd == "Add")
            {
                updateAdd(root, data1, data2);
            }
            else if(Cmd == "Sub")
            {
                updateSub(root, data1, data2);
            }
        }

    }

}

 

上面的代码总是超时，各种修改，各种去冗余还是超时。最后，我把所有的cout都改成了printf，尼玛居然就通过了!!!!! 时间从超过1000ms 缩短到了 412ms，

cout这也太慢了吧。AC代码如下：

#include <iostream>
#include <string>
using namespace std;

int Num[50001] = {0};
int sum;

typedef struct Node
{
    int left, right; //区间左右值
    int peopleNum; //区间总人数
    Node *pLeft, *pRight; //子区间指针
}Node;

Node * build(int l, int r) //建立线段树
{
    Node * root = (Node*)malloc(sizeof(Node));
    root->left = l;
    root->right = r;

    if(l == r)
    {
        root->peopleNum = Num[l];
        root->pLeft = NULL;
        root->pRight = NULL;
    }
    else
    {
        int mid = (r + l) >> 1;
        root->pLeft = build(l, mid);
        root->pRight = build(mid + 1, r);
        root->peopleNum = root->pLeft->peopleNum + root->pRight->peopleNum;
    }
    
    return root;
}

void updateAdd(Node * root, int group, int num)
{
    if(root->left == root->right)
    {
        root->peopleNum += num;
        return;
    }
    int m = (root->left + root->right) >> 1;
    if(group >= m + 1)
    {
        updateAdd(root->pRight, group, num);
    }
    else
    {
        updateAdd(root->pLeft, group, num);
    }
    root->peopleNum += num;
}


void getRangeNum(Node * root, int data1, int data2)
{
    if(data1 == root->left && data2 == root->right) //区间恰好重合
    {
        sum  += root->peopleNum;
        return;
    }
    int m = (root->left + root->right) >> 1;

    if(data1 > m) //都在右子树
    {
        getRangeNum(root->pRight, data1, data2);
    }
    else if(data2 <= m) //都在左子树
    {
        getRangeNum(root->pLeft, data1, data2);
    }
    else
    {
        getRangeNum(root->pLeft, data1, m);
        getRangeNum(root->pRight, m + 1, data2);
    }
}

int main()
{
    string Cmd;
    int N = 0; //总数据组数
    int ca = 0;
    cin >> N;

    while(N--)
    {
        //建立线段树
        int groupNum = 0;
        Node * root = NULL;
        Cmd = "";

        cin >> groupNum;
        for(int j = 1; j <= groupNum; j++)
        {
            cin >> Num[j];
        }
        root = build(1, groupNum);

        printf("Case %d:\n",++ca);  

        //处理查询、增减
        while(cin >> Cmd)
        {
            int data1, data2;
            if(Cmd == "Query")
            {
                sum = 0;
                cin >> data1 >> data2;
                getRangeNum(root, data1, data2);
                printf("%d\n", sum);
            }
            else if(Cmd == "Add")
            {
                cin >> data1 >> data2;
                updateAdd(root, data1, data2);
            }
            else if(Cmd == "Sub")
            {
                cin >> data1 >> data2;
                updateAdd(root, data1, -data2);
            }
            else
            {
                break;
            }
        }

    }

}