GIS原理篇 地图投影

一、地图投影的基础理论

1.1 大地水准面

大地水准面是地球重力场的等位面或水平面。想象一下海洋仅受重力的影响静止不动，而不受潮汐力和大气力的影响。隧道还用于连接海洋，以便海水能够自由流动。生成的表面是大地水准面的表现形式。大地水准面约等于平均海平面 (MSL)，通常与当地平均海平面有约一米的误差。它是一个复杂的形状。大地水准面受地球构造的影响，因此其坡度可能会不连续。这意味着该表面是与椭球体等数学表面相对的分析表面。大地水准面通常与地心水平大地基准面有不超过 100 米的误差。例如，在英国，大地水准面与水平基准面 (OSGB36) 相差不超过 5 米。

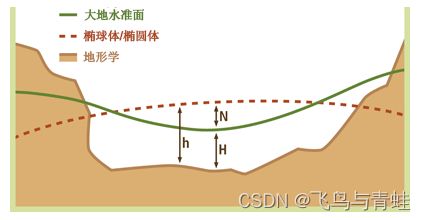
在上图中，绿色线代表大地水准面。它的曲线大致遵循地形的走向。虚线代表旋转椭球体的表面。“h” 是高出旋转椭球体或椭球体的高度 (HAE)。在本例中，高度是负值。“N” 代表大地水准面波动，它是旋转椭球体表面与大地水准面之间的距离。“H” 代表正高，它与旋转椭球体高度的关系如下所示：

h = H + N

1.2 椭球体

椭球体是通过二维椭圆创建的三维形状。椭圆是扁平化的圆形，具有一个长轴（较长的轴）和一个短轴（较短的轴）。如果旋转椭圆，旋转所形成的形状即为椭球体。椭圆中长半轴是长轴长度的一半。短半轴是短轴长度的一半。对于地球，长半轴是从地心到赤道的半径，短半轴是从地心到极点的半径。长半轴和短半轴的长度是区别椭球体的特征。

1.2.1 旋转椭球体和球体

地理坐标系表面的形状和大小由球体或旋转椭球体定义。尽管地球最适合用旋转椭球体表示，但有时将地球视作球体可使数学计算更为简便。对于小比例尺地图（小于 1:5,000,000）来说，可以将地球假设为球体。采用这种比例尺时，在地图上察觉不出球体与旋转椭球体的区别。但是，为了保证大比例尺地图（比例尺为 1:1,000,000 或更大）的精度，必须使用旋转椭球体表现地球的形状。在这种比例尺中，选择使用球体还是旋转椭球体取决于地图的用途以及数据的精度。

1.2.1.1 旋转椭球体的定义

球体以圆为基础，而旋转椭球体（或椭球体）以椭圆为基础。

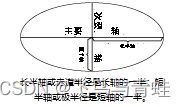
椭圆形状由两个半径定义。较长的半径称为长半轴，而较短的半径称为短半轴。

将椭圆绕短半轴旋转将生成旋转椭球体。旋转椭球体也称为旋转扁椭球体。下图显示了旋转椭球体的长半轴和短半轴。

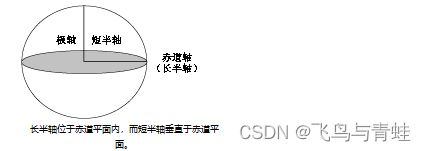
旋转椭球体由长半轴 a 和短半轴 b 定义，或者由 a 和扁率定义。扁率是两个轴长度的差异，以分数或小数表示。扁率 f 的计算公式如下：

f = (a - b) / a

扁率是一个较小的值，因而通常采用的是量 1/f。以下是 1984 世界坐标系（WGS 1984 或 WGS84）的旋转椭球体参数：

a = 6378137.0 meters
b = 6356752.31424 meters
1/f = 298.257223563

扁率取值范围为 0 到 1。扁率值 0 表示两个轴相等，即球体。地球扁率约为 0.003353。另一个用来描述旋转椭球体形状的量（类似扁率）是偏心率的平方 e2。其计算公式如下：

1.3 基准面

基准面构建于所选椭球体之上，它可以包含局部高程变化。由于椭球体由椭圆旋转形成，因此得到的整个地球表面都是完全平滑的。但是这样并没有真实地反映实际情况，所以局部基准面可以包含局部高程变化。

当一个旋转椭球体的形状与地球相近时，基准面用于定义旋转椭球体相对于地心的位置。基准面给出了测量地球表面上位置的参考框架。它定义了经线和纬线的原点及方向。

当更改基准面或修正基准面时，地理坐标系（数据的坐标值）将发生改变（应为原点、反向不同）。

1.3.1 地心基准面

在过去的 15 年中，卫星数据为测地学家提供了新的测量结果，用于定义与地球最吻合的、坐标与地球质心相关联的旋转椭球体。地球中心（或地心）基准面使用地球的质心作为原点。最新开发的并且使用最广泛的基准是 WGS 1984。它被用作在世界范围内进行定位测量的框架。

1.3.2 区域基准面

局域基准面是在特定区域内与地球表面极为吻合的旋转椭球体。旋转椭球体表面上的点与地球表面上的特定位置相匹配。该点也被称作基准面的原点。原点的坐标是固定的，所有其他点由其计算获得。

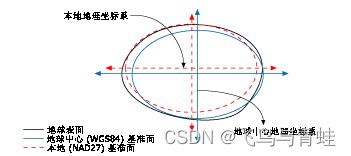
区域基准面的坐标系原点不在地心上。区域基准面的旋转椭球体中心距地心有一定偏移。因为区域基准面的旋转椭球体只与地表某特定区域吻合得很好，所以它不适用于该区域之外的其他区域。

二、地图投影

2.1 什么是地图投影

地图投影是利用一定数学法则把地球表面的经、纬线转换到平面上的理论和方法。

2.2 为什么要进行地图投影

由于地球是一个赤道略宽两极略扁的不规则的梨形球体，故其表面是一个不可展平的曲面，所以运用任何数学方法进行这种转换都会产生误差和变形（测量需要），为按照不同的需求缩小误差（缩小测量误差），就产生了各种投影方法。按变形性质，地图投影可分为四类：等角投影、等（面）积投影等距投影和任意投影。

2.3 地图投影的类型

2.3.1 为什么会有多种投影类型

无论将地球视为球体还是旋转椭球体，都必须变换其三维曲面以创建平面地图图幅。此数学变换通常称作地图投影。理解地图投影如何改变空间属性的一种简便方法就是观察光穿过地球投射到表面（称为投影曲面）上。想像一下，地球表面是透明的，其上绘有经纬网。用一张纸包裹地球。位于地心处的光会将经纬网投影到一张纸上。现在，可以展开这张纸并将其铺平。纸张上的经纬网形状与地球上的形状不同。地图投影使经纬网发生了变形。

展平旋转椭球体并不比展平橙皮容易，因为它会破裂。用两种尺寸表示地球表面会导致数据的形状、面积、距离或方向发生变形。

地图投影使用数学公式将地球上的球面坐标与平面坐标关联起来。

不同投影会引起不同类型的变形。有些投影旨在最大限度地降低一种或两种数据特的变形。投影可保持要素面积不变，但会改变其形状。在下图中，极点附近的数据已被拉伸。

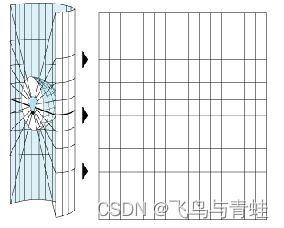
下图显示了如何压缩三维要素以拟合到平面上。

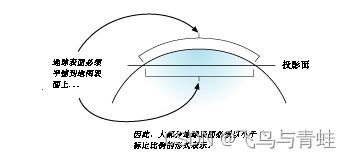
地图投影具有特定用途。一种地图投影可能用于限定区域中的大比例尺数据，而另一种地图投影则用于小比例尺的世界地图。针对小比例尺数据的地图投影通常基于球体地理坐标系而不是椭球体地理坐标系。

2.3.2 投影类型

2.3.2.1 等角投影

等角投影保留局部形状。要保留描述空间关系的各个角，等角投影必须在地图上显示以 90 度角相交的垂直经纬网线。地图投影通过保持所有角不变来加以实现。缺点是由一些弧线围起来的区域将在此过程中发生巨大变形。地图投影无法保留较大区域的形状。

2.3.2.2 等积投影

等积投影保留所显示要素的面积。为此，形状、角和比例等其他属性将发生变形。在等积投影中，经线和纬线可能不垂直相交。有些情况下，尤其是较小区域的地图，形状不会明显变形，且很难区分等积投影和等角投影，除非加以说明或进行测量。

2.3.2.3 等距投影

等距地图保留某些点间的距离。任何投影都无法在整幅地图中正确保持比例不变。不过，多数情况下，地图上总会存在一条或多条这样的线：比例沿着这些线将正确地保持不变。多数等距投影都具有一条或多条这样的线：在此类线中，地图上线的长度（按地图比例尺计算）与地球上同一条线的长度相同，无论它是大圆还是小圆，是直线还是曲线。此类距离被视为真实距离。例如，在正弦投影中，赤道和所有纬线就是其真实长度。在其他等距投影中，赤道和所有经线具有真实长度。而其他投影（例如，两点等距离）仍会显示地图上一点或两点与相隔点间的真实比例。请记住，任何投影都不能实现地图上的所有点是等距离的。

2.3.2.4 真方向投影

曲面（例如，地球）上两点间的最短路径是沿平面上直线的球面等价线。即，两点所在的大圆。真方向（或方位）投影维持某些大圆圆弧不变，从而能够相对于中心正确地给出地图上所有点的方向或方位角。某些真方向投影也是等角、等积或等距投影。

三、投影参数

仅有地图投影并不足以定义投影坐标系。可以声明数据集处于横轴墨卡托投影中，但这些信息并不充足。投影中心在哪？是否使用了比例尺因子？如果不知道投影参数的精确值，就无法重新投影数据集。这就需要投影参数，通过投影参数可以了解投影对数据造成的变形程度。

每种地图投影都有一组必须定义的参数。参数用于指定原点以及为感兴趣区域自定义投影。角度参数使用地理坐标系单位，而线性参数使用投影坐标系单位。

3.1 线性参数

东移假定值是应用到 x 坐标原点的线性值。北移假定值是应用到 y 坐标原点的线性值。

通常使用东移假定值和北移假定值来确保所有 x 值和 y 值都是正数。也可以使用东移假定值和北移假定值参数来缩小 x 坐标值或 y 坐标值的范围。例如，如果知道所有 y 值均大于 5,000,000 米，则可使用 -5,000,000 的北移假定值。

在垂直近侧透视投影中，高度定义球体或旋转椭球体表面上方的透视点。

3.2 角度参数

• 方位角定义投影的中心线。旋转角度用于测量北偏东方向的角度。它在洪特尼斜轴墨卡托投影、改良斜正形投影和局部投影中与方位角配合使用。
• 中央子午线定义 x 坐标的原点。
• 起始经度定义 x 坐标的原点。中央子午线与起始经度参数同义。
• 中央纬线定义 y 坐标的原点。
• 起始纬度定义 y 坐标的原点。此参数可能并不在投影中心。特别地，圆锥投影使用此参数设置感兴趣区域下 y 坐标的原点。在这种情况下，不需要设置北移假定值参数来确保所有 y 坐标都是正数。
• 中心经度与洪特尼斜轴墨卡托投影中心（两点和方位角）配合使用来定义 x 坐标的起点。它通常与起始经度和中央子午线参数同义。
• 中心纬度与洪特尼斜轴墨卡托投影中心（两点和方位角）配合使用来定义 y 坐标的原点。它几乎总是投影的中心。
• 标准纬线 1 和标准纬线 2 与圆锥投影配合使用来定义比例为 1.0 的纬线。使用一条标准纬线定义兰勃特等角圆锥投影时，第一条标准纬线定义 y 坐标的原点。

对于其他圆锥投影来说，y 坐标原点由起始纬度参数确定。

• 第一点的经度
• 第一点的纬度
• 第二点的经度
• 第二点的纬度

以上四个参数在两点等距投影和洪特尼斜轴墨卡托投影中使用。它们指定两个用来定义投影中心轴的地理点。

• 伪标准纬线 1 用于在 Krovak 投影中定义斜圆锥的标准纬线。
• XY 平面旋转定义 Krovak 投影的方向，以及 x 和 y 比例参数。

3.3 无单位参数

• 比例尺因子是应用于地图投影中心点或中心线的无单位值。
  比例尺因子通常略小于 1。使用横轴墨卡托投影的通用横轴墨卡托 (UTM) 坐标系的比例尺因子为 0.9996。沿投影中央子午线的比例是 0.9996，而不是 1。这将创建两条几乎平行的线，它们距比例为 1.0 的位置大约 180 千米（或约 1°）。该比例尺因子减小了感兴趣区域上投影的总体变形程度。
• 在 Krovak 投影中使用 X 比例和 Y 比例对轴进行定向。
• 在立方体投影和富勒投影中，使用选项参数。在立方体投影中，使用选项定义极面的位置。在富勒投影中，当选项为 0 时，将显示所有 20 个面。指定 1 到 20 之间的某个选项值将显示单一面。在立方体投影中，有效的选项值介于 0 到 15 之间。

三、坐标系

3.1 什么是坐标系

坐标系 GCS（Geographic Coordinate System）全称地理坐标系统，是用于表示地理要素、影像和观测结果（如通用地理框架内的 GPS 位置）的参考系统。坐标系（地理坐标系或投影坐标系）为定义真实世界的位置提供了框架，使地理数据集可使用公共位置进行集成。每个坐标系通过以下几方面定义：

• 测量框架，可以是地理框架（从地心开始测量球面坐标），也可以是平面框架（将地球的坐标投影到二维平面上）。
• 测量单位（通常对于投影坐标系为英尺或米，对于经纬度为十进制度数）。
• 投影坐标系的地图投影定义。
• 其他测量系统属性，例如参考椭圆体、基准面以及一条或多条标准纬线、中央经线和 x 与 y 方向的可能位移之类的投影参数。

3.2 坐标系类型

GIS 中使用两种常用的坐标系类型：

• 全局坐标系或球坐标系，例如经纬度。这些坐标系通常称为地理坐标系。
• 基于横轴墨卡托、亚尔勃斯等积或罗宾森等地图投影的投影坐标系，这些地图投影（以及其他多种地图投影模型）提供了各种机制将地球球面的地图投影到二维笛卡尔坐标平面上。投影坐标系有时称为地图投影。

3.3 地理坐标系

地理坐标系 (GCS) 使用三维球面来定义地球上的位置。GCS 往往被误称为基准面，而基准面仅是 GCS 的一部分。GCS 包括角度测量单位、本初子午线和基准面（基于旋转椭球体）。

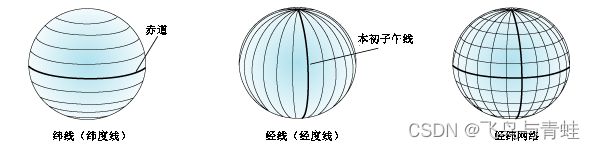
可通过其经度和纬度值对点进行引用。经度和纬度是从地心到地球表面上某点的测量角。通常以度或百分度为单位来测量该角度。下图将地球显示为具有经度和纬度值的地球。

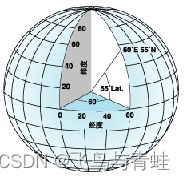
在球面系统中，水平线（或东西线）是等纬度线或纬线。垂直线（或南北线）是等经度线或经线。这些线包络着地球，构成了一个称为经纬网的格网化网络。

位于两极点中间的纬线称为赤道。它定义的是零纬度线。零经度线称为本初子午线。对于绝大多数地理坐标系，本初子午线是指通过英国格林尼治的经线。其他国家/地区使用通过伯尔尼、波哥大和巴黎的经线作为本初子午线。经纬网的原点 (0,0) 定义在赤道和本初子午线的交点处。这样，地球就被分为了四个地理象限，它们均基于与原点所成的罗盘方位角。南和北分别位于赤道的下方和上方，而西和东分别位于本初子午线的左侧和右侧。

通常，经度和纬度值以十进制度为单位或以度、分和秒 (DMS) 为单位进行测量。维度值相对于赤道进行测量，其范围是 -90°（南极点）到 +90°（北极点）。经度值相对于本初子午线进行测量。其范围是 -180°（向西行进时）到 180°（向东行进时）。如果本初子午线是格林尼治子午线，则对于位于赤道南部和格林尼治东部的澳大利亚，其经度为正值，纬度为负值。

用 X 表示经度值并用 Y 表示纬度值可能会有帮助。这样，显示在地理坐标系上定义的数据就如同度是线性测量单位一样。此方法与普通圆柱投影基本相同。
尽管使用经度和纬度可在地球表面上定位确切位置，但二者的测量单位是不同的。只有在赤道上，一经度所表示的距离才约等于一纬度所表示的距离。这是因为，赤道是唯一一条长度与经线相同的纬线。（其半径与球面地球半径相同的圆称为大圆。赤道和所有经线都是大圆。）

在赤道上方和下方，用来定义纬度线的圆将逐渐变小，直到最终在南极点和北极点处变为一个点，所有经线均在此处相交。由于经线沿极点方向逐渐集中，所以一经度所表示的距离最终将减小为零。在 Clarke 1866 旋转椭圆体上，赤道上的一经度等于 111.321 km，而在纬度为 60° 度位置，只有 55.802 km。因为经度和纬度不具有标准长度，所以无法对距离或面积进行精确测量，或者无法很容易地在平面地图或计算机屏幕上显示数据。

3.4 投影坐标系

投影坐标系在二维平面中进行定义。与地理坐标系不同，在二维空间范围内，投影坐标系的长度、角度和面积恒定。投影坐标系始终基于地理坐标系，而后者则是基于球体或旋转椭球体的。

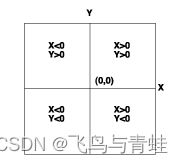
在投影坐标系中，通过格网上的 x,y 坐标来标识位置，其原点位于格网中心。每个位置均具有两个值，这两个值是相对于该中心位置的坐标。一个指定其水平位置，另一个指定其垂直位置。这两个值称为 x 坐标和 y 坐标。采用此标记法，原点坐标是 x = 0 和 y = 0。

在等间隔水平线和垂直线的格网化网络中，中央水平线称为 x 轴，而中央垂直线称为 y 轴。在 x 和 y 的整个范围内，单位保持不变且间隔相等。原点上方的水平线和原点右侧的垂直线具有正值；下方或左侧的线具有负值。四个象限分别表示正负 X 坐标和 Y 坐标的四种可能组合。

在地理坐标系中处理数据时，有时用 X 轴表示经度值并用 Y 轴表示纬度值很有用。

四、地理变换

地理坐标系定义了一个用于标识 3D 地球上各位置点的框架。每个地理坐标系 (GCS) 都具有一个设置了大小和形状的椭圆体。每个地理坐标系也以某种特定方式与地球紧密相关。因此，地面上的同一位置在不同地理坐标系中将具有不同的坐标值。如果在投影坐标系中显示数据，这种差异会被放大，可能从几厘米到几百米不等。如果使用基于不同地理坐标系的数据集，则需要设置地理（或基准面）变换。

***注意：如果某对地理坐标系之间不具有任何变换，可能需要使用第三个地理坐标系来构建一系列变换。

4.1 基于方程的方法

基于方程的变换方法可归类到以下四种方法类型。

4.1.1 三参数方法

最简单的基准面变换方法是地心（或三参数）变换。地心变换在 XYZ 或 3D 直角坐标系中对两个基准面间的差异情况进行建模。定义一个基准面使其中心为 0,0,0。相距一定距离定义另一个基准面（dx,dy,dz 或 ΔX,ΔY,ΔZ，单位为米）。

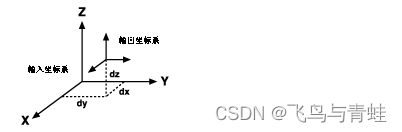
通常，变换参数被定义为“从”区域基准面“到”1984 世界坐标系 (WGS) 或另一个地心基准面。

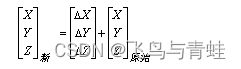
三个参数是线性平移量并且始终以米为单位。

4.1.2 七参数方法

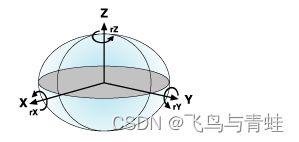
通过对地心变换再增加四个参数可实现更复杂和精确的基准面变换。七个参数是指三个线性平移量 (dx,dy,dz)、绕各轴的三个角度旋转值 (rx,ry,rz) 和一个比例尺因子。

旋转值以十进制秒为单位给定，而比例尺因子采用百万分率 (ppm)。旋转值有两种不同的定义方法：朝 XYZ 系统原点方向看时顺时针为正或逆时针为正。

前面的方程表示美国和澳大利亚定义方程的方式，称为坐标框架旋转变换。逆时针旋转为正。欧洲使用称为位置矢量变换的另一种约定。这两种方法有时被称为布尔沙-沃尔夫方法。在投影引擎中，坐标框架和布尔沙-沃尔夫方法完全相同。坐标框架和位置矢量方法均受支持，并且通过更改三个旋转值的符号可以很方便地将变换值从一种方法转换到另一种方法。例如，对于坐标框架方法，从 WGS 1972 基准面转换到 WGS 1984 基准面的所用参数（顺序为 dx,dy,dz,rx,ry,rz,s）是：

(0.0, 0.0, 4.5, 0.0, 0.0, -0.554, 0.227)

要在位置矢量方法中使用相同的参数，请更改旋转值的符号，新参数如下：

(0.0, 0.0, 4.5, 0.0, 0.0, +0.554, 0.227)

无法单从参数确定正在使用哪种约定。如果使用错误的方法，结果将返回不精确的坐标。确定参数定义方式的唯一方法是在两个系统中检查坐标为已知的控制点。

4.2 基于格网的方法

略