用R和BioConductor进行基因芯片数据分析(四):芯片内归一化
接前一篇: 用R和BioConductor进行基因芯片数据分析(三):计算median
归一化是从normalization翻译过来的。归一化的目的是使各次/组测量或各种实验条件下的测量可以相互比较,消除测量间的非实验差异。非实验差异可能来源于样品制备,点样,杂交过程,杂交信号处理等。
归一化的方法有很多,对于寡聚核苷酸芯片(单通道,以Affymetrix为代表)和cDNA芯片(双通道,红绿染料)也有所不同。以下讨论针对双通道芯片进行,当然也可能适用于单通道,请读者自辨。
归一化通常分为bulk normalization和control-based normalization. 前者假定仅有一小部分基因表达值在不同条件下有差异,因此使用所有的基因作为标准进行归一化;而后者使用表达值被认为是不变的那些对照基因作为标准进行归一化。这2种方法的假设前提都未必时时成立,因此需要具体情况具体分析。
“bulk” normalization又细分为许多方法,最简单的就是global normalization,这种方法假设红色染料的信号强度与绿色染料的信号强度是正相关的,即R=kG (R:红色信号强度,G:绿色信号强度,k:常数),因此表达信号强度的以2为底的对数比log ratio在归一化之后相当于平移了一个常量c=logk:log(R/G) → log(R/G) – c = log(R/G) – logk = log[R/(kG)].
c的计算方法通常是用所有红色信号强度和除以所有绿色信号强度和然后取以2为底的对数,即c=log[total(R)/total(G)]
Intensity-dependent normalization通常比global normalization更好,因为后者的假设通常并不完全正确,通常情况下,log ratio是和信号强度值有关的,即log(R/G) → log(R/G) – c(A),这里A=1/2*log(R*G),是log product intensity或简称log intensity。
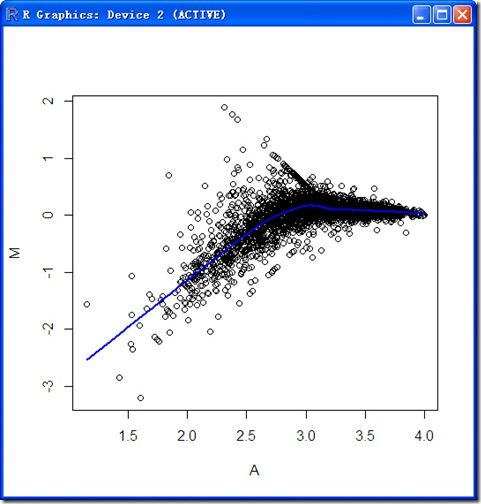
对于我们的数据mediandata,我们可以直观的看到log ratio和信号强度的关系:
上图叫做MA-plot(MA图),纵坐标是M=log(R/G)=log(new/old),横坐标是A=1/2*log(R*G)=1/2*log(new*old)。
其中的蓝色曲线是lowess回归函数(什么是lowess)。(注:由于原始数据有5行有0值,导致有些M或A=Inf或-Inf,无法进行Lowess回归,因此人工删除了这5行,处理后的中位数数据mediandata在这里下载。当然你也可以用原始数据求出M和A值,自己删除Inf值对应的mediandata中的行。
在R中画出上图的代码:
mediandata<-read.table('mediandata.txt',header=TRUE)
mediandata<-mediandata[,-1] #移除第一列ID列
MA<-matrix(data = NA, nrow =dim(mediandata)[1], ncol = dim(mediandata)[2], byrow = TRUE, dimnames = NULL)
new<-0
old<-0
for (i in 1:dim(mediandata)[1]){
for (j in 1:(dim(mediandata)[2]/2)){
new<-mediandata[i,2*j-1]
old<-mediandata[i,2*j]
MA[i,2*j]<-log(new/old)/log(2) #M=log(new/old)/log2
MA[i,2*j-1]<-1/2*log(new*old)/log(2) #A=1/2*log(new*old)/log2
}
}
plot(MA[,1],MA[,2],xlab='A',ylab='M')
lines(lowess(MA[,1],MA[,2],f=0.2,iter=2),lwd=2,col='blue')
#仅画出第一张芯片上2个杂交样本的MA图,使用MA[,3],MA[,4]可以画出第2张芯片的图,依此类推。
可以看出原始数据的log ratio受到log intensity的影响,因此需要intensity-based normalization.
R的lowess函数返回一个$y对象,储存每个A值(lowess返回的$x对象)对应的~M值,而归一化后的M’=M-~M=M-$y($x)
这样归一化后得到10个芯片的log ratio即10列数据,但是为了后面分析的方便,我想得到10个new的强度值和10个old的强度值共20列数据,那怎么办呢?
答案很简单,就是假设new的强度值在归一化后不变,而仅仅改变old的强度值,得到old’=old*2^($y($x)) 注:$y($x)是2的指数,推导很简单
下面是R代码:
normed<-matrix(data = NA, nrow =dim(MA)[1], ncol = dim(MA)[2], byrow = TRUE, dimnames = NULL) #new—奇数列; old—偶数列
for (j in 1:(dim(MA)[2]/2)){
out_lowess<-lowess(MA[,2*j-1],MA[,2*j],f=0.2,iter=2)
#A=MA[,1],M=MA[,2]
loc_lowess<-cbind(out_lowess$x,out_lowess$y)
for (i in 1:dim(MA)[1]){
normed[i,2*j-1]<-mediandata[i,2*j-1] #归一化后的new’强度值
normed[i,2*j]<-mediandata[i,2*j]*2^(loc_lowess[,2][loc_lowess[,1]==MA[i,2*j-1]][1]) #归一化后的old’强度值
}
}
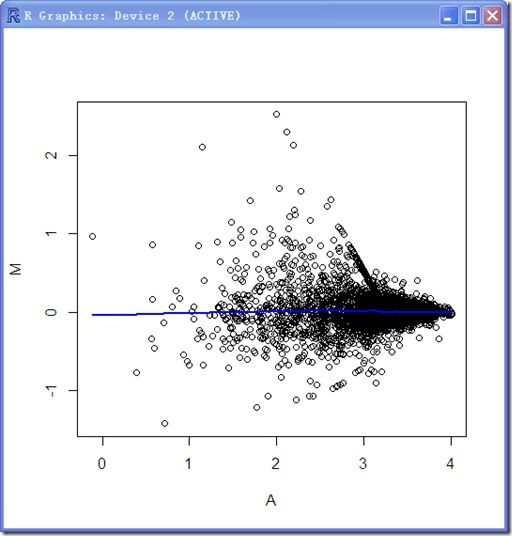
搞定,看看效果吧:
MAnormed<-matrix(data = NA, nrow =dim(MA)[1], ncol = 2, byrow = TRUE, dimnames = NULL)
MAnormed[,2]<-log(normed[,1]/normed[,2])/log(2) #M=log(new/old)/log2
MAnormed[,1]<-1/2*log(normed[,1]*normed[,2])/log(2) #A=1/2*log(new*old)/log2
plot(MAnormed[,1],MAnormed[,2],xlab='A',ylab='M')
lines(lowess(MAnormed[,1],MAnormed[,2],f=0.2,iter=2),lwd=2,col='blue')
现在的lowess回归曲线是一条直线了,说明归一化后的log ratio与强度值无关了。
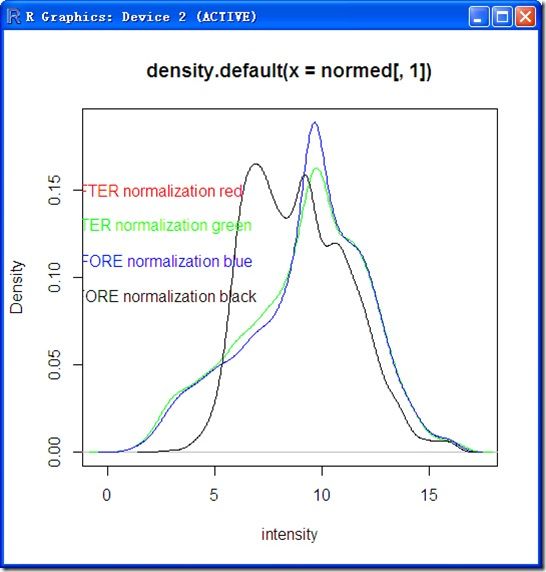
可以从另一个角度看归一化的效果:
plot(density(normed[,1]),type='line',col='red',xlab='intensity')
points(density(normed[,2]),type='line',col='green')
points(density(mediandata[,1]),type='line',col='blue')
points(density(mediandata[,2]),type='line',col='black')
text(2.2,c(0.09,0.11,0.13,0.15),labels=c('BEFORE normalization black','BEFORE normalization blue','AFTER normalization green','AFTER normalization red'),col=c('black','blue','green','red'))
关于芯片内归一化,可以参考以下资料:
cDNA双通道芯片:
Yang Y.H., Dudoit S., Luu P., Speed T.P. (2001) Normalization for cDNA microarray data, SPIE BiOS 2001, San Jose CA;
Yang Y.H., Dudoit S., Luu P., Lin D.M., Peng V., Ngai J., Speed T.P. (2002), Normalization for cDNA microarray data: a robust composite method addressing single and multiple slide systematic variation, Nucleic Acids Research 30(4);
寡聚核苷酸单通道芯片:
Bolstad B.M., Irizarry R. A., Astrand M., Speed T.P. (2003) A comparison of normalization methods for high density oligonucleotide array data based on bias and variance, Bioinformatics 19(2): 185-193