python机器学习之支持向量机——线性SVM决策过程的可视化案例
线性SVM决策过程的可视化
1、导入需要的模块
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
2、实例化数据集,可视化数据集
X,y = make_blobs(n_samples=50, centers=2, random_state=0,cluster_std=0.6)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")#rainbow彩虹色
plt.xticks([])
plt.yticks([])
plt.show()
3、画决策边界:理解函数contour
matplotlib.axes.Axes.contour([X, Y,] Z, [levels], **kwargs)
#首先要有散点图
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax= plt.gca() #获取当前的子图,如果不存在,则创建新的子图
4、 画决策边界:制作网格
#获取平面上两条坐标轴的最大值和最小值
xlim = ax.get_xlim()
ylim = ax.get_ylim()
#在最大值和最小值之间形成30个规律的数据
axisx = np.linspace(xlim[0],xlim[1],30)
axisy = np.linspace(ylim[0],ylim[1],30)
axisy,axisx = np.meshgrid(axisy,axisx)
#我们将使用这里形成的二维数组作为我们contour函数中的X和Y
#使用meshgrid函数将两个一维向量转换为特征矩阵
#核心是将两个特征向量广播,以便获取y.shape * x.shape这么多个坐标点的横坐标和纵坐标
xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
#其中ravel()是降维函数,vstack能够将多个结构一致的一维数组按行堆叠起来
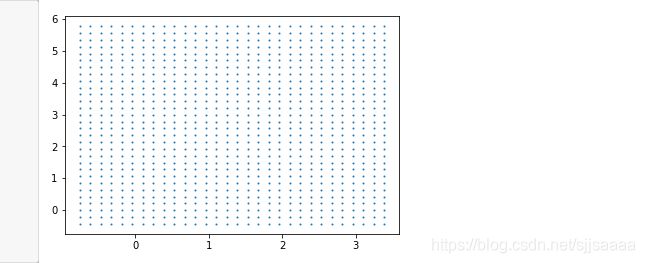
#xy就是已经形成的网格,它是遍布在整个画布上的密集的点
plt.scatter(xy[:,0],xy[:,1],s=1,cmap="rainbow")
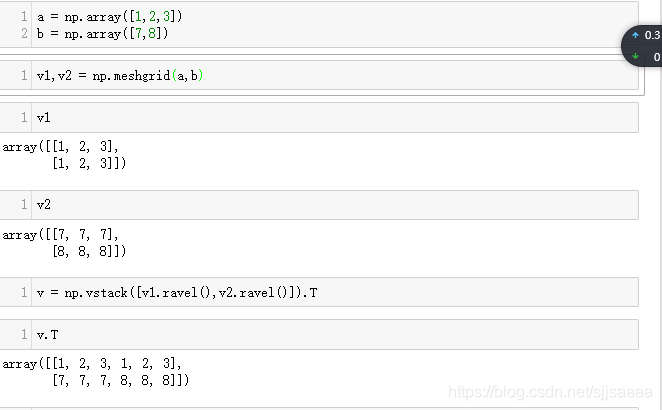
#理解函数meshgrid和vstack的作用
a = np.array([1,2,3])
b = np.array([7,8])
#两两组合,会得到多少个坐标?
#答案是6个,分别是 (1,7),(2,7),(3,7),(1,8),(2,8),(3,8)
v1,v2 = np.meshgrid(a,b)
v1
v2
v = np.vstack([v1.ravel(), v2.ravel()]).T
5、建模,计算决策边界并找出网格上每个点到决策边界的距离
#建模,通过fit计算出对应的决策边界
clf = SVC(kernel = "linear").fit(X,y)#计算出对应的决策边界
Z = clf.decision_function(xy).reshape(axisx.shape)
#重要接口decision_function,返回每个输入的样本所对应的到决策边界的距离
#然后再将这个距离转换为axisx的结构,这是由于画图的函数contour要求Z的结构必须与X和Y保持一致
#首先要有散点图
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca() #获取当前的子图,如果不存在,则创建新的子图
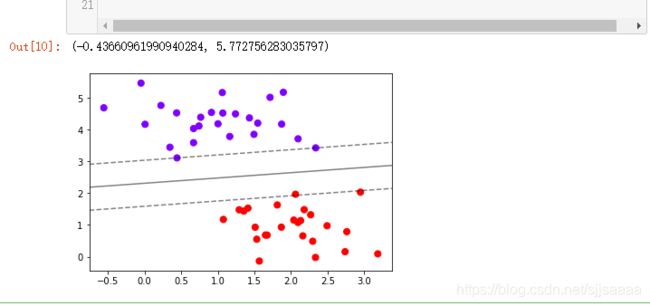
#画决策边界和平行于决策边界的超平面
ax.contour(axisx,axisy,Z
,colors="k"
,levels=[-1,0,1] #画三条等高线,分别是Z为-1,Z为0和Z为1的三条线
,alpha=0.5#透明度
,linestyles=["--","-","--"])
ax.set_xlim(xlim)#设置x轴取值
ax.set_ylim(ylim)
#Z的本质是输入的样本到决策边界的距离,而contour函数中的level其实是输入了这个距离
#让我们用一个点来试试看
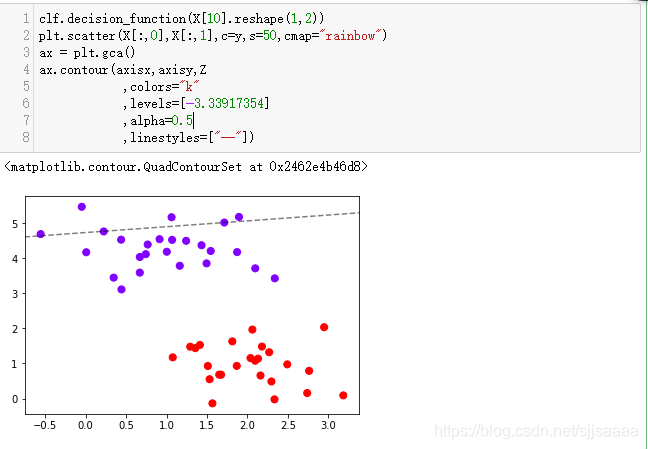
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plt.scatter(X[10,0],X[10,1],c="black",s=50,cmap="rainbow")
clf.decision_function(X[10].reshape(1,2))
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca()
ax.contour(axisx,axisy,Z
,colors="k"
,levels=[-3.33917354]
,alpha=0.5
,linestyles=["--"])
6、将绘图过程包装成函数
#将上述过程包装成函数:
def plot_svc_decision_function(model,ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
x = np.linspace(xlim[0],xlim[1],30)
y = np.linspace(ylim[0],ylim[1],30)
Y,X = np.meshgrid(y,x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
ax.contour(X, Y, P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
#则整个绘图过程可以写作:
clf = SVC(kernel = "linear").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
7、探索建好的模型
clf.predict(X)
#根据决策边界,对X中的样本进行分类,返回的结构为n_samples
clf.score(X,y)
#返回给定测试数据和标签的平均准确度
clf.support_vectors_
#返回支持向量坐标
clf.n_support_#array([2, 1])
#返回每个类中支持向量的个数
8、推广到非线性情况
from sklearn.datasets import make_circles
X,y = make_circles(100, factor=0.1, noise=.1)
X.shape
y.shape
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plt.show()
clf = SVC(kernel = "linear").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
clf.score(X,y)
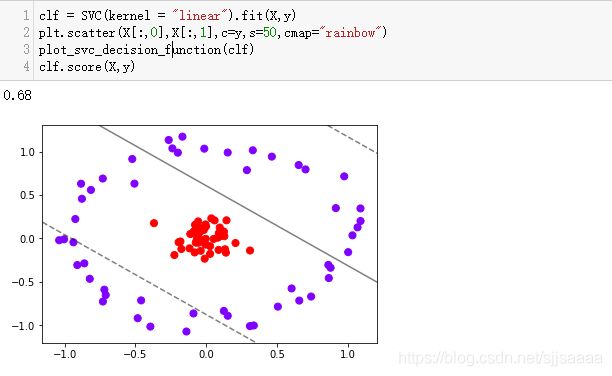
明显,现在线性SVM已经不适合于我们的状况了是两种类别。这个时候,如果我们能够在原本的据,来看看添加维度让我们的数据如何变化。
9、为非线性数据增加维度并绘制3D图像
#定义一个由x计算出来的新维度r
r = np.exp(-(X**2).sum(1))
rlim = np.linspace(min(r),max(r),100)
from mpl_toolkits import mplot3d
#定义一个绘制三维图像的函数
#elev表示上下旋转的角度
#azim表示平行旋转的角度
def plot_3D(elev=30,azim=30,X=X,y=y):
ax = plt.subplot(projection="3d")
ax.scatter3D(X[:,0],X[:,1],r,c=y,s=50,cmap='rainbow')
ax.view_init(elev=elev,azim=azim)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("r")
plt.show()
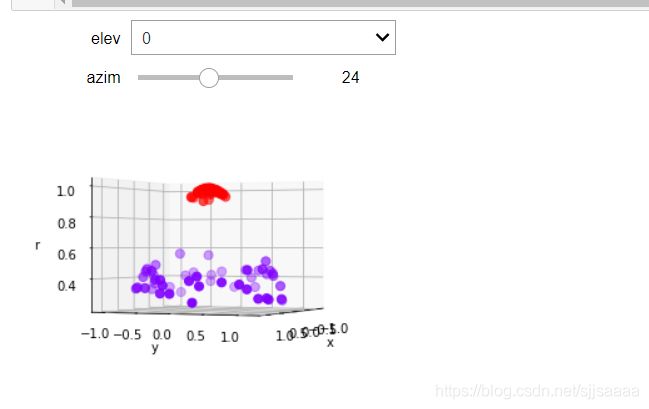
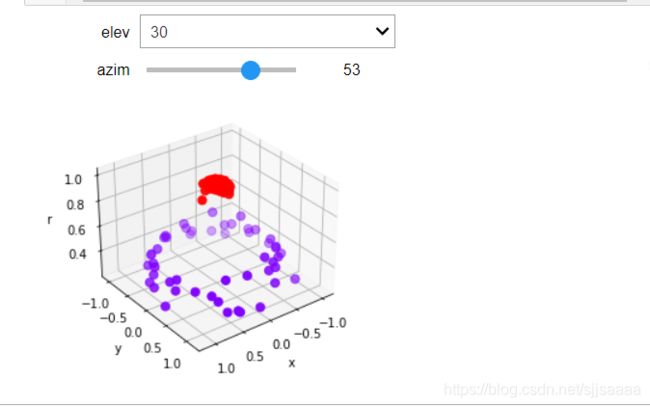
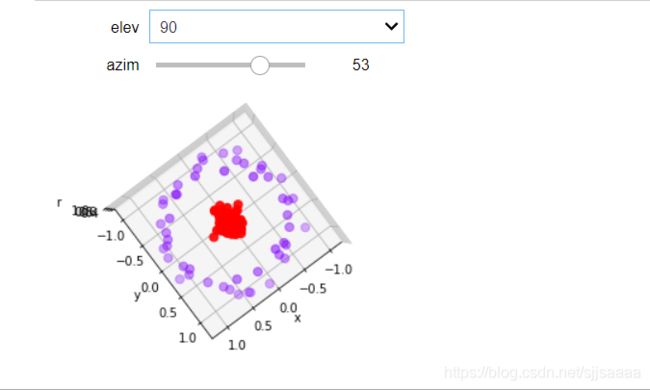
plot_3D()
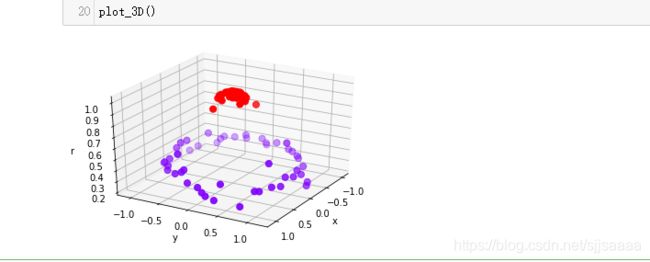
可以看见,此时此刻我们的数据明显是线性可分的了:我们可以使用一个平面来将数据完全分开,并使平面的上方的所有数据点为一类,平面下方的所有数据点为另一类。
10、 将上述过程放到Jupyter Notebook中运行
#如果放到jupyter notebook中运行
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_circles
X,y = make_circles(100, factor=0.1, noise=.1)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
def plot_svc_decision_function(model,ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
x = np.linspace(xlim[0],xlim[1],30)
y = np.linspace(ylim[0],ylim[1],30)
Y,X = np.meshgrid(y,x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
ax.contour(X, Y, P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
clf = SVC(kernel = "linear").fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
plot_svc_decision_function(clf)
r = np.exp(-(X**2).sum(1))
rlim = np.linspace(min(r),max(r),100)
from mpl_toolkits import mplot3d
def plot_3D(elev=30,azim=30,X=X,y=y):
ax = plt.subplot(projection="3d")
ax.scatter3D(X[:,0],X[:,1],r,c=y,s=50,cmap='rainbow')
ax.view_init(elev=elev,azim=azim)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("r")
plt.show()
from ipywidgets import interact,fixed
interact(plot_3D,elev=[0,30,60,90],azip=(-180,180),X=fixed(X),y=fixed(y))
plt.show()
明显我们可以用一个平面将两类数据隔开,这个平面就是我们的决策边界了。