强化学习学习笔记

强化学习

一.基本概念

1.什么是强化学习：

• 个体主动对环境作试探而不是静止地被动地等待
• 环境对试探动作产生的反馈是评价性的，个体根据环境的评价来调整以后的行为，是一种从环境状态到行为映射的学习。
  
  一个以“打翻水杯”为例的机器-环境交互的例子：
  
  
  注：
• 结合两幅图可以发现这是一个连续的过程
• 这个状态是环境的状态，而不是机器的状态，实质上是机器的一个observation.

AlphaGo的示例：


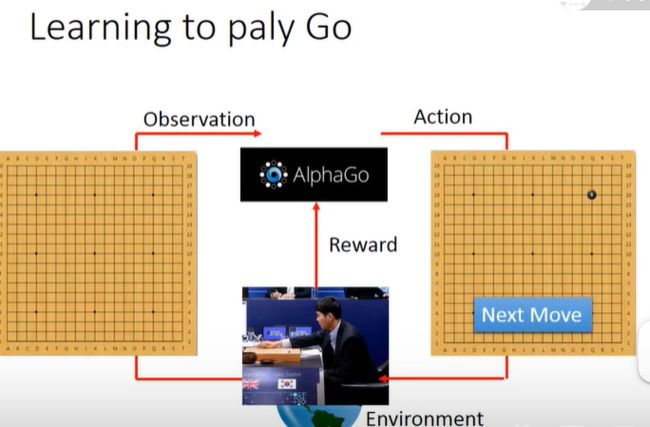
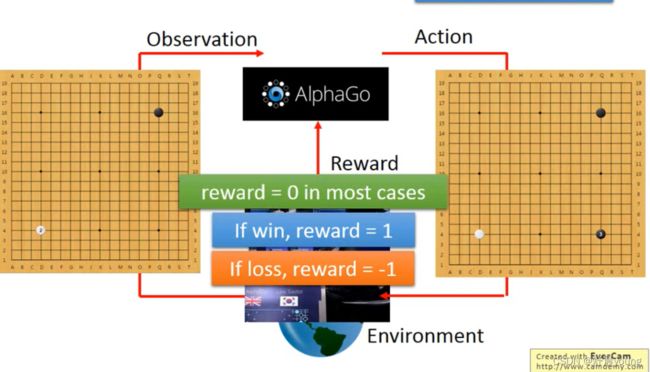
在大多数情况下reward都是0，这个过程中机器需要做的一个事情就是通过调整模型，学习在什么状态下应该采取什么行动可以使得期望reward取得一个最大值。
AlphaGo的实际操作过程是令两个机器做对手下棋来进行学习。

2.用马尔可夫决策过程(MDP) 的描述方式：
机器处于环境E中，状态空间为X，其中每个状态x∈X是机器感知到的环境的描述；机器能采取的动作构成动作空间A，若某个动作a∈A作用在当前状态x上，则潜在的转移函数P使得环境从当前状态按某种概率转移到另一个状态；在转移到另一个状态的同时，环境会根据潜在的“奖赏”函数R反馈给机器一个奖赏。
综合起来对应一个四元组：E=
主要是表示机器和环境交互的整个过程
eg:给西瓜浇水问题的MDP：

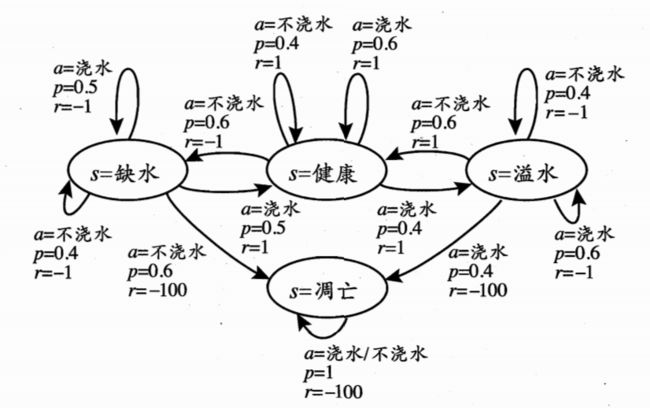
MDP本质：
设系统在某任意时刻t的状态为s,则机器在t时刻执行动作a后使状态转变为下一状态s’的概况P(s’|s,a)，以及获得的瞬时奖赏值r(s,a)都仅仅依赖于当前状态s和选择的动作a,而与历史状态和历史动作无关，即“将来”与“现在”有关，而与“过去”无关。
3.机器与环境：
（机器只能做出行动、接受结果，不能决定行动对应啥结果） 在环境中状态的转移、奖赏的返回是不受机器控制的；机器只能通过选择要执行的动作来影响环境，只能通过观察转移后的状态和返回的奖赏来感知环境。
机器的任务：在环境中不断尝试学得策略$\pi$（用函数或者概率表示）,这个决策使得在某状态下就能得知要执行的动作。
关于策略：

• 在每一个状态都会给出一个动作，是一个状态到动作映射的函数
• 输出的是在当前状态所有可能动作的概率分布
• 表现形式：$\pi (a|s)=P(A_t=a|S_t=s)$
• 还有一个假设是策略函数是静态的，不同时间上概率分布是独立的。

策略的优劣标准：长期执行后得到的累计奖赏。计算方式：

• T步累积奖赏：$E[\frac{1}{T}{\sum }_{t=1}^T{r}_t]$
• $\gamma$折扣累积奖赏:$E[{\sum }_{t=0}^{+\infty }{\gamma }^t{r}_{t+1}]$

4.强化学习任务：
找到能使长期累积奖赏最大化的策略。
total reward期望值的计算：

$\tau$是一次执行的序列（过程），把每一步的奖赏加起来就是$R(\tau )$,我们希望的就是这个玩意儿的期望值可以最大，在参数$\theta$下所求的期望值等于每一个过程发生的概率与该过程的总奖赏的乘积。
我们不可能罗列某策略下所有的可能序列，因此实质上是在该策略下进行N次，获得N个过程，对这N个过程的总奖赏求平均。

5.强化学习与监督学习

• 模型的形式无差别（状态–示例，动作–标记，策略–分类器or回归器）
• 监督学习是希望使得total loss最小，强化学习是希望total reward期望值最大
• 强化学习中并没有监督学习中的有标记样本，机器只有通过“反思”之前的动作是否正确来学习什么状态下该做什么动作。可看作“延迟标记信息”的监督学习问题。
• 什么状态应该对应什么动作有时候是提前不知道的，这类场景下监督学习的方法受限，可以用强化学习，因为它是从experiment中进行学习。

6.强化学习面临的困难

一是奖赏存在延迟，也就是主体动作存在潜在的影响未来奖赏的可能，不止影响立即得到的奖励，而且影响接下来的动作和最终的奖励，但是现在看不出来；另一方面机器的动作会影响它接收到的后面的数据信息，比如有些东西是它没探索过的，就无法获知这种情形下会有什么奖赏
7.强化学习方法分类

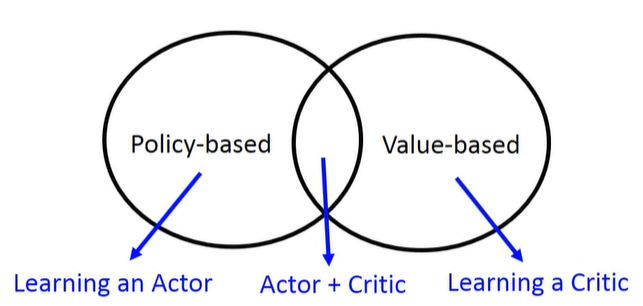
基于策略的方法学习的是采取何种行动，希望学得策略，以状态为输入，然后以动作为输出，奖赏用来帮助选择最优的一个function.
基于值的方法学的是批评，评价现在的行为有多好或者有多不好，而不学习采取什么行动。

除了这种分类方式，其实还有其他的分类方式：比如可以分为有模型学习方法和免模型学习方法

二.K-摇臂赌博机（单步强化学习任务理论模型）

考虑最大化单步奖赏（也可以认为是在选择有价值的数据的方式）

• “仅探索”法：轮流按下每个摇臂，最后以每个摇臂各自的平均吐币概率作为其奖赏期望的近似估计。（仅为获知每个摇臂的期望奖赏的方法，会失去很多选择最优摇臂的机会）
• “仅利用”法：按下到目前为止平均奖赏最大的摇臂（仅为执行奖赏最大的动作的方法，没有很好地估计期望奖赏）

事实上，面临“探索-利用”窘境。搜索新动作（试错）可以带来长期的性能改善，帮助收敛到最优策略，但是探索多了有可能找到差的动作；利用（强化）可以帮助系统短期性能改善，但可能收敛到次优解，但是探索少了有可能错过好的动作。
所以欲累积奖赏最大，必须在两者之间达成较好折中。

1.$ϵ$-贪心
基于一个概率来对探索和利用进行折中：
每次尝试时，以$ϵ$的概率进行探索（以均匀概率随机选取一个摇臂）；以$1-ϵ$的概率进行利用（选择当前平均奖赏最高的摇臂。摇臂奖赏不确定性较大时，需要更多的探索，则需要较大的$ϵ$值；反之需要的$ϵ$值较小。（可以令$ϵ=1/\sqrt{t}$）

尝试n次,得到奖赏$v_1,...,v_n,$摇臂k的平均奖赏：$$Q(k)=\frac{1}{n}\sum _{i=1}^n{v}_i$$
第n次更新：$$Q_n(k)=\frac{1}{n}((n-1)\times Q_{n-1}(k)+v_n)=Q_{n-1}(k)+\frac{1}{n}(v_n-Q_{n-1}(k))$$（这样只需要记录次数和最近平均奖赏）

算法描述：

2.Softmax
基于当前已知的摇臂平均奖赏来进行折中：
平均奖赏相当则被选取概率也相当，平均奖赏高的摇臂被选取概率也更高。
摇臂概率分配基于Boltzmann分布：

其中$\tau$越小则平均奖赏高的摇臂被选取的概率越高 （$\tau$越小，那么俩个不同的Q值使得P值相差越大） $\tau$趋于0是算法趋于“仅利用”，趋于无穷大时算法趋于“仅探索”。

算法描述：

三.有模型学习

考虑多步强化学习任务，假定模型已知。(机器已对环境进行了建模，能在机器内部模拟出与环境相同或近似的状况，此时$P_{x\to x^{\prime }}^a$和$R_{x\to x^{\prime }}^a$已知）

1.策略评估 （基于值的方法）
在给出的一个策略$\pi$基础上，对策略$\pi$估计它带来的期望累积奖赏。

• 状态值函数$V^{\pi }(x)$:从状态x出发，使用策略$\pi$带来的期望累积奖赏
  
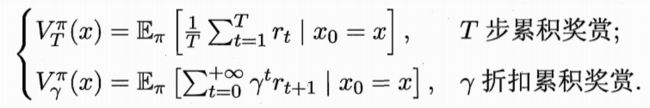
  ①$\gamma$是一个折扣量，取值范围[0,1],根据步骤对奖励进行一定折扣计算在t步骤的收益（在一段时间内的奖励函数加权平均值）$$r_1+\gamma r_2+{\gamma }^2{r}_3+..$$奖励有累积，但是会随着时间衰减，更重视当前奖励；避免出现带环马尔可夫过程中的无穷奖励；为0表示只关注当前奖励，为1表示同样程度地关心未来奖励
• 状态-动作值函数$Q^{\pi }(x,a)$:从状态x出发，执行动作a后再使用策略$\pi$带来的累积奖赏(一个从现在开始到结束的累积的期望）
  

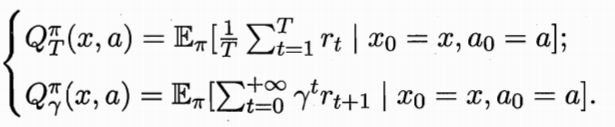
状态值函数与Q函数的关系：对Q函数进行边缘概率求和得到V函数（结合一个图感受一下）：

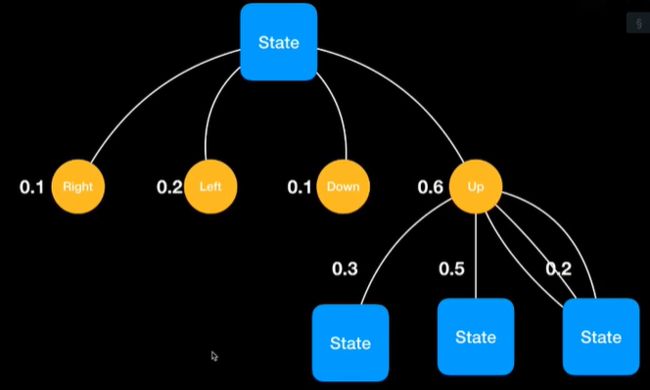
对于最上面那个状态，会有一个动作的概率分布，动作确定后就会得到一个Q函数

贝尔曼方程
主要定义当前状态和外来状态之间的一个关联。
根据马尔可夫性质（系统下一时刻的状态仅由当前时刻状态决定），状态值函数的递归形式：

算法描述：

对于$V_{\gamma }^{\pi }$,由于${\gamma }^t$在t很大时趋于0，因此也能使用类似算法，将(16.7)换成(16.8)即可。

算法迭代的停止准则：可以设一个阈值$\theta$,然后把第四行条件替换为：

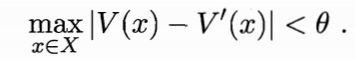
有了状态值函数V后，可直接计算出状态-动作值函数：

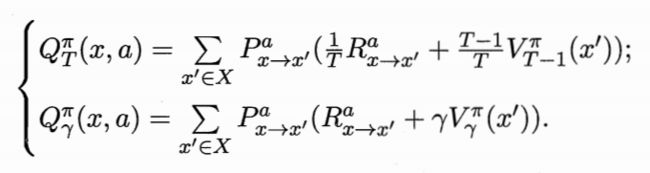
2.策略改进
理想的策略应能最大化累积奖赏：$${\pi }^{\ast }={\mathrm{argmax}}_{\pi }\sum _{x\in X}{V}^{\pi }(x)$$ (对所有的初始状态经过策略$\pi$后计算累计奖赏，然后把它们加起来)
最优值函数：最优策略对应的值函数
最优Bellman等式：

这一块前面提到的递归式相当于是考虑了每个可能的动作带来的累计奖赏，对每个求出来的值乘了该动作发生的概率；最优值函数里面则是直接选择了令$V_T^{\ast }(x)$最大的那个动作。

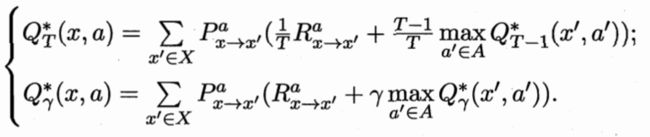
最优Bellman等式揭示了非最优策略的改进方式：将策略选择的动作改变为当前最优的动作。

3.策略迭代与值迭代（在MDP中的方法）

动态规划方法：把一个复杂的问题变为相对简单的一些子问题，再利用保存解决这些子问题得到结果来减少运算复杂度。
强化学习中的动态规划：

• 预测：评估一个策略
• 控制：找到一个最优策略

获取最优策略：

• 直接在动作价值函数获取最大化值
• 当$a=argma{x}_{a\in A}{Q}_{\pi }(x,a)$时，${\pi }^{\ast }(x,a)=1$否则为0

策略迭代：不断迭代进行策略评估和改进，直到策略收敛、不再改变为止。
基于T步累积奖赏的策略迭代算法 算法描述：

基于T步累积奖赏的值迭代算法算法描述：

四.免模型学习

学习算法不依赖于环境建模。
1.蒙特卡罗强化学习
是一种模型无关的，解决基于平均样本回报的强化学习问题的学习方法。
策略评估替代方法：多次“采样”，然后求取平均累积奖赏作为期望累积奖赏的近似。
在模型未知的情形下，从起始状态出发，使用某种策略进行采样，执行该策略T步并获得轨迹$$<x_0,a_0,r_1,x_1,a_1,r_2,...,x_{T-1},a_{T-1},r_T,xT>$$对轨迹中每一对状态-动作，记录之后的奖赏之和，作为该状态-动作对的一次累积奖赏采样值。多次采样得到多条轨迹后，将每个状态-动作对的累积奖赏采样值进行平均，即得到状态-动作值函数的估计。

估计状态值函数：

• 在完成一次迭代中每一步t状态是可以观察的
• 增加迭代次数：N(s)=N(s)+1
• 增加总的回报：S(s)=S(s)+G(t)
• 计算回报的均值：v(s)=S(s)/N(s)
• 当N(s)趋于∞，v(s)趋于$v_{\pi }$

2.TD
可以看成是MC和DP算法的一个折中算法。

Sarsa
推导TD目标：

$\gamma$折扣累积奖赏：$U_t^{\pi }=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+...$
提出一个$\gamma$ 之后: $$U_t^{\pi }=R_t+\gamma （R_{t+1}+\gamma R_{t+2}+...)=R_t+\gamma U_{t+1}^{\pi }$$假设$r_t$依赖于t时刻的状态、动作、下一时刻的状态:($S_t,A_t,S_{t+1}$)
$Q^{\pi }(s_t,a_t)=E[U_t^{\pi }|s_t,a_t]=E[R_t+\gamma U_{t+1}^{\pi }|s_t,a_t]$
把两项期望分解开来：$$Q^{\pi }(s_t,a_t)=E[R_t|s_t,a_t]+\gamma E[U_{t+1}^{\pi }|s_t,a_t]$$而 $E[U_{t+1}^{\pi }|s_t,a_t]=E[Q^{\pi }(S_{t+1},A_{t+1})|s_t,a_t]$
所以可以写成$$Q^{\pi }(s_t,a_t)=E[R_t+\gamma Q^{\pi }(S_{t+1},A_{t+1})]$$直接求期望很困难，所以对期望做蒙特卡洛近似：把$R_t$近似为观测到的奖励$r_t$,用观测到的$s_{t+1}和a_{t+1}$代替随机变量$S_{t+1}和A_{t+1}$
TD 目标：$$y_t=r_t+\gamma Q^{\pi }(s_{t+1},a_{t+1})$$TD学习是希望$Q^{\pi }(s_t,a_t)更接近y_t$

表格形式的Sarsa：



$\alpha$是一个学习率

Q-learning:
用来学习最优状态-动作值函数$Q^{\ast }(s,a)$
推导TD目标：

AlphaGo

大体思路：
训练

• 模仿人类学习，初始化策略网络（实质上是一种监督学习）
• 用强化学习进一步学习策略网络（使用的是策略梯度方法，策略网络自我博弈）
• 训练价值网络（使用了策略网络）

实施

• 使用策略网络和价值网络，通过蒙特卡罗搜索树搜索

参考资料：

【1】西瓜书
【2】李宏毅强化学习系列网课
【3】https://www.bilibili.com/video/BV1Qt411j7e6?p=2
【4】https://www.bilibili.com/video/BV1rv41167yx?p=5
（以上是一些主要的资源与网课链接，侵权删减）