深度之眼Paper带读笔记GNN.06.GAT

前言

本课程来自深度之眼，部分截图来自课程视频。

文章标题：Graph Attention Networks
图注意力网络（GAT）
作者：Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, Yoshua Bengio
单位：MILA(Montreal Institute of Learning Algorithms)
发表会议及时间：ICLR 2018
公式输入请参考：在线Latex公式
要通过本文了解图神经网络的消息传递方式，汇聚每个节点邻域中的特征。是后面学习GCN和GraphSage的基础。

导读

论文结构

摘要：介绍背景及提出GAT模型，图卷积神经网络网络模型，在节点特征从邻居汇聚的时候考虑权重，适用于直推式和归纳式。
Introduction：介绍图的广泛应用，以及如何将卷积操作应用到图上，介绍基于空域和频域的两类方法，介绍注意力机制，引出本文的模型GAT 。这篇文章的introduction也很有意思，把通常的related works也包含在里面了，这节的递进关系：CNN→图表示→GNN→过渡段提GNN分类：频域和空域→频域工作→空域工作→注意力机制→小结→本工作与前面研究的关系。
GAT Architecture：GAT模型结构并和之前的模型做对比。
Evaluation：实验部分，数据集介绍，baselines选取，直推式和归纳式两种实验方式，图的节点分类效果对比。
Conclusion：总结提出了的GAT模型使用了注意力机制，邻居汇聚时考虑不同的权重同时具有归纳式学习的能力，讨论几种未来方向如模型可解释性和图的分类。

学习目标

研究背景

从研究GNN的目标来说，就是想要获取图中节点，边的embedding表示，然后可以做downstream的任务。通常的思路如下图所示，将图中节点或边映射到低维空间中。

那么节点的相似度就可以表示为：
$$\text{similarity}(u,v)\approx z_v^{\top }{z}_u$$
上图中的$\text{ENC}(v)=z_v$代表的就是Encoder，对图进行Encoder通常就是使用graph neural networks（GNN）：multiple layers of non-linear transformations of graph structure.这个想法最初是从CNN的卷积演化而来：

从上图可以看出，二者都是从邻居表示过来的，一个的邻居是像素，一个的邻居是节点：
1.In CNN, pixel representation is created by transforming neighboring pixel representation.
2.In GNN,node representations are created by transforming neighboring node representation But graphs are irregular,unlike images. So, generalize convolutions beyond simple lattices, and leverage node features/attributes. Solution:deep graph encoders.
当然，图可以用邻接矩阵表示（特征可以加到右边列中），然后丢给NN去训练：
这样理论是没什么问题，但是这样做有几个问题：
1.空间复杂度高，需要$O(|V|)$个参数空间。
2.图的大小是不固定的，而NN的结构不好改变，改变需要重新训练。
3.对于图而言，其访问序列是位置相关的（邻接矩阵位置不能随意调整），而NN吃的样本往往和输入位置无关（随机采样）。
Idea:Generate node embeddings based on local network neighborhoods.
-A node’s neighborhood defines its computation graph.
因此这里我们采用结点的邻居来表征结点，采用1跳邻居或者2跳邻居来表征，则和GNN的层数/深度（不是卷积核）有关。
Learn how to aggregate information from the neighborhood to learn node embeddings.
只不过不同模型采用了不同的方式将邻居信息汇集到当前节点中，但总体思想是一样的，都可以用如下方式来表示：
Transform information from the neighbors and combine it:
邻居信息为$h_i$，传递或者说表征到当前节点可以看做一个线性变换（这里省略了bias）： $W_i{h}_i$
·Transform “messages” $h_i$ from neighbors: $W_i{h}_i$.

图卷积

A desirable form of a graph convolutional operator.
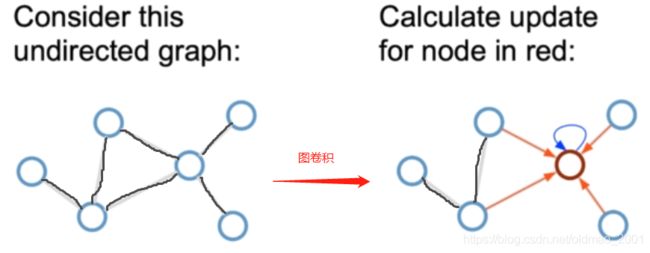
把邻居节点看做是图像的pixels，如果卷积核大小或者说范围是一跳邻居，那么中心节点可以用avgpooling（取周围一跳邻居的平均），maxpooling（取周围一跳邻居的最大值）。这篇文章要用attention，那么必然是对周围邻居做不同的权重，再进行计算。下图是一个具体的例子，A是要求embedding的节点，范围为一跳，因此它可以由BCD三个节点做avgpooling后，进NN的神经元操作（灰色方块），同理BCD三个节点又有各自一跳节点汇聚计算得来

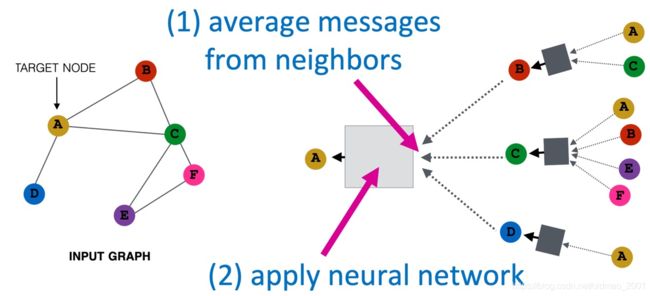
Notation

Assume we have a graph $G$:
-$V$ is the vertex set
-$A$ is the adjacency matrix (assume binary)
-$X\in R^{m\times |V|}$ is a matrix of node features（这个是新加的东西，代表节点特征，$V$个节点，每个节点特征为$m$维，应该是$|V|\times m$，这里做了转置，不同的网络可以有不同的特征）
-Social networks: User profile, User image
-Biological networks: Gene expression profiles
-If there are no features, use:
· Indicator vectors(one-hot encoding of a node)
· Vector of constant $1:[1,1,..\dots ,1]$

归纳式学习

GAT，GraphSage都属于这个类型，当我们针对某个图训练好一个模型后（生成该图对应embedding），我们可以用其来生成一个新的图（这个图模型未看过）的embedding，生成的规则是从原来图中学习到的点的汇聚方式之类的东西。

E.g., train on protein interaction graph from model organism A and generate embeddings on newly collected data about organism B.

空域与频域卷积

GCN可以看做空域也可以看做频域，从空域看它是将邻居信息汇聚到当前节点，然后将其公式经过严格的数学变化则可以推导出频域卷积的公式。大部分空域的GNN都可以用本文提到的消息传递机制实现。
从下图可以看到，在频域卷积上的研究还不多。

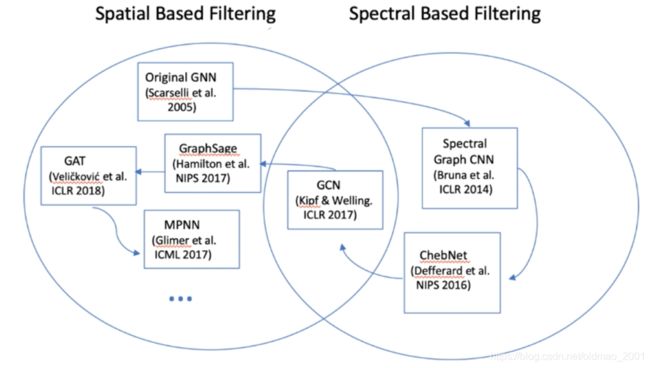
GAT模型多头注意力机制

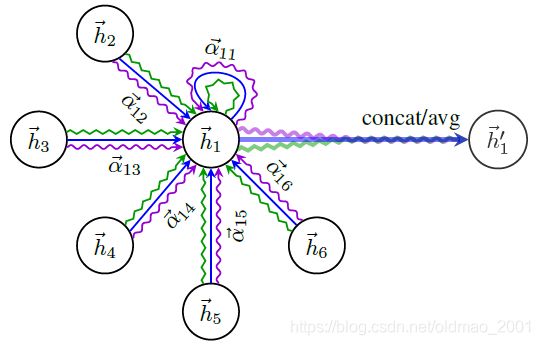
先来看一个注意力机制如何运作，以蓝色直箭头为例，上图中$h_1$的下一个时刻状态为$h_1^{\prime }$，$h_1^{\prime }$是由$h_1$本身以及其他邻居的信息按权重${\alpha }_{1i}^1$汇聚而来的，${\alpha }_{11}^1$代表$h_1$本身和$h_1$进行汇聚的权重，${\alpha }_{12}^1$代表$h_1$和$h_2$进行汇聚的权重，以此类推。这里权重的上标代表多头注意力的标号，这里代表1号箭头，还可以由2号、3号箭头。
上图中有三种箭头，代表汇聚了三次，每次汇聚的权重都不一样，这样就有了三头注意力。

意义

图卷积神经网络最常用的几个模型之一（GCN，GAT，GraphSAGE）
将attention机制引用到图神经网络中
早期图神经网络表征学习的代表性工作，后期作为经典baseline
支持直推式学习和归纳式学习
模型具有一定的可解释性

泛读

摘要

1. 本文提出了图注意力网络（GAT），在图结构数据上使用注意力机制。
   We present graph attention networks (GATs), novel neural network architectures that operate on graph-structured data, leveraging masked（相当于只在一跳邻居进行attention） self-attentional（对自身也有attention操作） layers to address the shortcomings of prior methods based on graph convolutions or their approximations.
2. 为邻域中的不同节点指定了不同的权重，计算效率高同时不需要预先知道图结构。
   By stacking layers in which nodes are able to attend over their neighborhoods’ features, we enable (implicitly) specifying different weights to different nodes in a neighborhood, without requiring any kind of costly matrix operation (such as inversion) or depending on knowing the graph structure upfront.
3. GAT模型可以适用于直推式和归纳式学习。
   In this way, we address several key challenges of spectral-based graph neural networks simultaneously, and make our model readily applicable to inductive as well as transductive problems.
4. GAT算法在多个图数据集上达到最优效果。
   Our GAT models have achieved or matched state-of-theart results across four established transductive and inductive graph benchmarks: the Cora, Citeseer and Pubmed citation network datasets, as well as a proteinprotein interaction dataset (wherein test graphs remain unseen during training).

论文结构

1. Introduction
2. GAT architecture
   2.1Graph attention layer
   2.2 Comparisons to related work
3. Evaluation
   3.1Datasets
   3.2 State-of-the-art methods
   3.3 Experimental setup
   3.4Results
4. Conclusions

精读

算法模型总览

GAT算法知识树

根据原文2.1节的描述，GAT模型的输入节点特征集合，假设有N个节点，每个节点特征维度为F，则输入可以表示为：
$$h=\{h_1,h_2,...h_N\},h_i\in R^F$$
对于模型的输出而言，假设输出维度为F’，则输出可以表示为：
$$h^{\prime }=\{h_1^{\prime },h_2^{\prime },...h_N^{\prime }\},h_i^{\prime }\in R^{F^{\prime }}$$
线性变换的参数$W\in R^{F^{\prime }\times F}$，输入经过线性变换$Wh$得到的维度就是F’,

GNN的结构

与普通NN不一样，普通NN中的每一层都是自己定义的，例如CNN，输入层，卷积层，池化层，各个层多少大小什么的。在GNN中，它把每次卷积作为一层，每个时间步会经过一个卷积操作，例如下面这个无向图的节点v：

它的下一层就是从v节点自己本身（绿色箭头）以及周围邻接一跳节点获取消息（蓝色箭头），进行卷积计算，更新自己的state（或者说embedding？）更新后的维度和原来维度不一样：

GCN算法对传入v的五个消息都是同等看待，每个消息都有1/5的权重；
GAT算法则引入注意力机制，为每个消息根据重要性分配（学习到）不同的权重。
更新完这一层之后，还可以再重复一次这样的卷积操作，就是还有一层，一般就到这里结束。
下面看例子：

Building Block of GCNs
For each node in the graph,a convolutional operator consists of two main steps:
1.Aggregation of neighbouring node features. （不用学习参数，只涉及邻接矩阵）
2.Applying a nonlinear function to generate the output features.（非线性变换参数）
Complete GCN consists of multiple convolutional layers.（每个节点都有一个卷积层）
在这里我们通常用$H^{(l)}$表示第$l^{th}$层
$W_0^{(l)}$和$W_1^{(l)}$是每一层学习的参数，前者对应当前节点本身的影响，后者对应邻居节点的影响，这两组参数是对所有节点shared的。
$A$为邻接矩阵，$D$为度对角矩阵，对角线上的值为当前节点的邻居（度）个数
GCN的向量表示为：
$$H^{(l+1)}=\sigma (H^{(l)}{W}_0^{(l)}+\tilde{A}{H}^{(l)}{W}_1^{(l)})\text{\hspace{1em}(1)}$$

$$\tilde{A}=D^{\frac{1}{2}}A{D}^{-\frac{1}{2}}\text{\hspace{1em}(2)}$$
这里面$\sigma$是非线性函数；
$H^{(l)}{W}_0^{(l)}$是对自身节点的非线性变换
$\tilde{A}{H}^{(l)}{W}_1^{(l)})$是对当前节点的所有邻居节点非线性变换
$$H^{(l)}=[h_1^{(l{)}^T}{]}^T......h_N^{(l{)}^T}{]}^T$$
大H是小h即每个节点的embedding堆叠起来的，如果写成单个节点：
$$h_i^{(l+1)}=\sigma (h_i^{(l)}{W}_0^{(l)}+\sum _{j\in N_i}\frac{1}{c_{ij}}{h}_j^{(l)}{W}_1^{(l)})$$
其中$N_i$表示邻居节点
$j\in N_i$表示属于邻居节点的节点$j$
$h_j$就是邻居节点$j$的特征表示
$\frac{1}{c_{ij}}$表示对邻居节点的归一化（每个节点的邻居节点数量不一样，直接求和不公平）

如果把公式1和2进行一个变化，把对自身的影响合并到邻居影响那项：

$$H^{(l+1)}=\sigma (\hat{A}{H}^{(l)}{W}^{(l)})\text{\hspace{1em}(3)}$$
$$\hat{A}={\tilde{D}}^{\frac{1}{2}}(A+I_N){\tilde{D}}^{-\frac{1}{2}}$$
$I_N$就是单位对角矩阵（斜线上都1，其他位置都0的矩阵）
具体推导先挖坑，等GCN再填

GAT算法

GAT结构中最主要就是attention的部分：
$$H_i^{(l+1)}=\sigma (\sum _{j\in N_{(i)}}{\alpha }_{ij}^{(l)}{H}_j^{(l)}{W}^{(l)})\text{\hspace{1em}(5)}$$
公式5就是GAT的卷积公式，其中的${\alpha }_{ij}$就是attention的权重，该权重如下图所示：

数学表达就是：
$${\alpha }_{ij}=f(H_{i}W,H_{j}W)$$
f简单理解就是对当前节点i和邻居节点j求余弦相似度，W是线性变换。上边的左图是具体算的例子
先把$W{h}_i$和$W{h}_j$concat起来，上图中是两个4维的，拼成8维的（下式7中中括号内的操作），然后和向量$a$（维度是8*1）进行点乘（下式7中括号内的操作），结果是一个标量，在经过一个leakyReLU（下式7中的操作），然后再经过softmax得到这里的softmax是针对所有i的邻接点来做的（公式6的操作），具体数学表示为：
$${\alpha }_{ij}=softmax(e_{ij})=\frac{e_{ij}}{exp({\sum }_{k\in N_{(i)}}{e}_{ik})}\text{\hspace{1em}(6)}$$

$$e_{ij}=LeakyReLU(a^T[H_{i}W,H_{j}W])\text{\hspace{1em}(7)}$$

---

另外一篇文章中用不同的attention计算公式，也可以：
$${\alpha }_{ij}=tanh((H_{i}W{)}^{T}C(H_{j}W))$$

---

$e_{ij}$是指点j的特征的对点i的重要性。为了保证图结构信息，这里只对节点i的邻居节点进行attention，即：masked attention.
最后，根据attention权重计算输出，对应原文公式4：
$$h_i^{\prime }=\sigma (\sum _{j\in N_i}{\alpha }_{ij}W{h}_j)$$
论文中还用到了多头，每一个头都是一组独立的attention权重，如果有8组，那么最后可以对8组结果拼接：
$$h_i^{\prime }={\parallel }_{k=1}^K\sigma (\sum _{j\in N_i}{\alpha }_{ij}{W}^k{h}_j)$$
拼接后的维度变成$K\times F^{\prime }$，如果觉得维度太大还可以求平均：
$$h_i^{\prime }=\sigma (\frac{1}{K}\sum _{k=1}^K\sum _{j\in N_i}{\alpha }_{ij}{W}^k{h}_j)$$

算法模型细节一：消息传递机制

Main idea Pass messages between pairs of nodes & agglomerate.
在上面的讲解中，我们只看到从邻居（一跳）从获取特征信息，其实不然，这里面存在多层邻居的特征信息都会汇聚到当前节点，现在看一个例子：

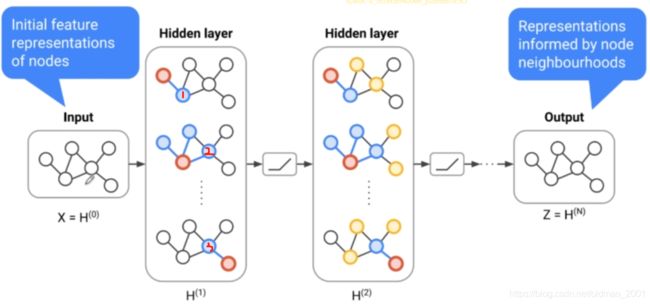
输入是一个图，然后经过第一个卷积操作后，可以看到图中有三个红色的点都接收到其一跳邻居蓝色点汇聚过来的信息，再经过第一个卷积操作后，由于在上一个时间步那些蓝色点也得到了他们邻居的信息，所以，这里再次从蓝色点汇聚到红色节点信息就包含了二跳邻居的信息。以此类推，这个操作其实和CNN的卷积一样，越到后面卷积看到的感受野就越大。

算法模型细节二：attention机制

这个在其他课程里面有讲，不深入了，摆几个例子。
对于CV：

对于NLP：

Seq2Seq：

几种经典的计算attention score的方法：

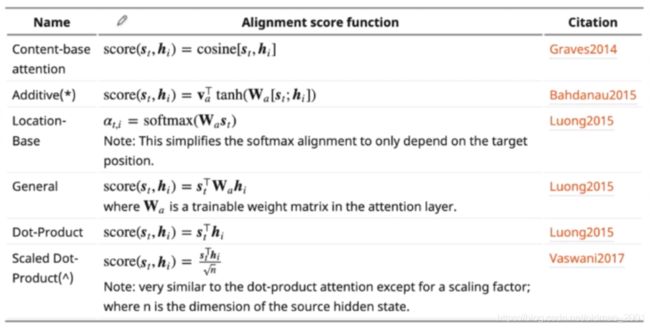
attention的类别

transform中的注意力机制有三个东西：QKV，本文中的attention直接用输入=Q=K=V进行计算。

算法模型细节三：多头注意力机制

略

算法模型细节四：直推式学习和归纳式学习

Transductive Learning Task：训练和预测都在同一张图上
·Training algorithm sees all node features during training
·Trains on the labels of the training Nodes

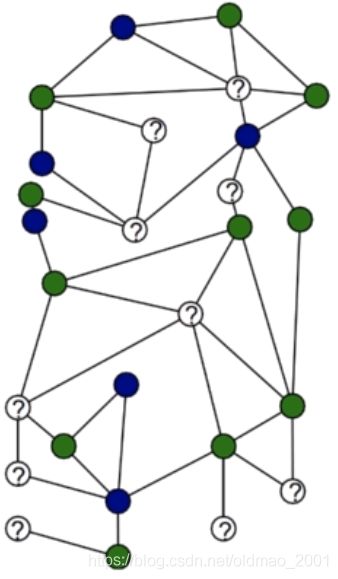
Inductive Learning Task训练和测试不在同一张图。
·Algorithm does not see test nodes during training
·Significantly more challenging than transductive task

算法模型细节五：GAT算法总结

对应原文2.2节
Computationally efficient
Neighbors different importances, interpretability （可解释性）
Shared manner for attention
GraphSAGE的缺点: fixed size neighbors（不能对所有邻居节点进行操作）+LSTM ordering issue（只能通过随机序列来缓解该问题）
这里要专门讲一下算法复杂度，该算法复杂度取决于attention的计算，即原文公式3：
$${\alpha }_{ij}=\frac{\exp \left(\text{LeakyReLU}(a^T[W{h}_i||W{h}_j])\right)}{{\sum }_{k\in N_i}\exp \left(\text{LeakyReLU}(a^T[W{h}_i||W{h}_k])\right)}$$

---

矩阵乘法时间复杂度：
$m\times k$的矩阵乘上$k\times n$的矩阵,得到$m\times n$的矩阵
复杂度是$O(m\times k\times n)$。

例如：
$(n\times 1)\cdot (1\times n)$时间复杂度就是$O(n^2)$
$(1\times n)\cdot (n\times 1)$时间复杂度就是$O(n)$。

---

分子中：输入$h_i$维度是$F\times 1$，参数$W$维度是$F^{\prime }\times F$，$W{h}_i$维度是$F^{\prime }\times 1$，时间复杂度是$O(F^{\prime }\times F\times 1)=O(F^{\prime }\times F)$，有V个点，所以
拼接后：$[W{h}_i||W{h}_j]$维度是$2F^{\prime }\times 1$，时间复杂度是$O(2F^{\prime }\times F\times 1)=O(F^{\prime }\times F)$，有$V$个顶点，要计算$V$次$F^{\prime }\times F$，时间复杂度为：$O(V\times F^{\prime }\times F)$。这里需要注意的是，分子分母都有要算$[W{h}_i||W{h}_j]$，我们只用算一次，所以这一块的时间复杂度也只记一次。

向量$a$维度是$2F^{\prime }\times 1$，转置后$a^T$是$1\times 2F^{\prime }$，故$a^T[W{h}_i||W{h}_j]$维度是1，就是常量，时间复杂度是$O(1\times 2F^{\prime }\times 1)$
非线性函数LeakyReLU是elementwise的操作，时间复杂度不变，还是$O(1\times 2F^{\prime }\times 1)$，可以写为$O(F^{\prime })$
这里算的是有相邻关系的节点的attention，如果a和b相邻（有一条边），那么就要算${\alpha }_{ab},{\alpha }_{ba}$两次，有$E$条边则时间复杂度为：$O(2E{F}^{\prime })=O(E{F}^{\prime })$

因此，GAT 的时间复杂度为 $O(|V|F{F}^{\prime }+|E|F^{\prime })$，其中 $|V|F{F}^{\prime }$是计算所有节点特征向量变换的时间复杂度 (即 $Wh$)，$|E|F^{\prime }$是计算 Attention 的时间复杂度。

实验结果及分析

数据集

这篇文章用了4个数据集，第一个数据集是重点，后面几篇文章都会用到，最后一个数据集（PPI是蛋白质结构图）是归纳式学习数据集，第三行表明该数据集共有24个图，本文用20个图做训练，2个图做验证，2个图做测试。

实验设置

对应原文3.3节，后面主要看直推式学习，归纳的就不详细讲了：
For the transductive learning tasks, we apply a two-layer GAT model. Its architectural hyperparameters have been optimized on the Cora dataset and are then reused for Citeseer.
用的是两层GNN模型，相当于可以汇聚两跳节点信息。
The first layer consists of $K=8$ attention heads computing $F^{\prime }=8$ features each (for a total
of 64 features), followed by an exponential linear unit (ELU) (Clevert et al., 2016) nonlinearity.
第一层用了8头注意力，每一个的输出维度$F^{\prime }=8$，一共64位，使用的非线性函数为ELU：

上图来自：https://www.cnblogs.com/jins-note/p/9646683.html
The second layer is used for classification: a single attention head that computes $C$ features (where $C$ is the number of classes), followed by a softmax activation.
第二层要用于分类，只用了一头注意力，输出维度为C维，C是数据集中的类别数量，最后跟一个softmax激活函数。
For coping with the small training set sizes, regularization is liberally applied within the model. During training, we apply $L_2$ regularization with $\lambda =0.0005$. Furthermore, dropout (Srivastava et al., 2014) with $p=0.6$ is applied to both layers’ inputs, as well as to the normalized attention coefficients (critically, this means that at each training iteration, each node is exposed to a stochastically sampled neighborhood).
在两个输入层上有用了抓爆，丢掉了一些邻居节点，相当于训练时从原有的邻居节点中随机采样出40%个节点进行计算。这个操作和the normalized attention coefficients一样。
Similarly as observed by Monti et al. (2016), we found that Pubmed’s training set size (60 examples) required slight changes to the GAT architecture: we have applied $K=8$ output attention heads (instead of one), and strengthened the $L_2$ regularization to $ \lambda= 0.001$. Otherwise, the architecture matches the one used for Cora and Citeseer.
Pubmed数据集在训练时对GAT参数进行了一点修改，这里不展开。

Both models are initialized using Glorot initialization (Glorot & Bengio, 2010) and trained to minimize cross-entropy on the training nodes using the Adam SGD optimizer (Kingma & Ba, 2014) with an initial learning rate of 0.01 for Pubmed, and 0.005 for all other datasets. In both cases we use an early stopping strategy on both the cross-entropy loss and accuracy (transductive) or micro-F1 (inductive) score on the validation nodes, with a patience of 100 epochs.
优化器采用的是Adam SGD，目标是最小化交叉熵，最后用了patience of 100 epochs.这个trick，相当于early stop，每次以100 epochs为单位来判断是否需要提前停止。

实验：节点分类任务

按Transductive和Inductive分别做了实验对比，其中星号代表该模型或方法所能达到的最好效果：


上图中倒数第二行是将权重设置为相同值得到的结果（相当于GCN模型）。
这里面对比的GraphSage用了多种更新方式，具体后面讲这个模型的时候再展开。

结果可视化

本文将第一个数据集的分类结果进行了可视化（t-SNE），每个颜色代表一种类别，然后每个节点之间还有线连接，这个线是模型在计算多头注意力的时候把所有头的注意力加起来（例如上面例子中3个箭头就是三头，三个箭头结果都可以加起来），按大小变成粗细画到图上。

论文总结

关键点
消息传递机制
模型的改进和区别
GAT模型结构和分析
创新点
Attention机制
Multi-head技术
直推式和归纳式
启发点
将深度学习的技术应用到图领域之中（attention之前在NLP、CV取得成功）
Attention机制的引入衡量了邻居的不同权重，有更好的解释性
直推式和归纳式的讨论，从图的设定上可以启发不同的工作
GAT广泛引入到各种应用问题
GCN、GAT、GraphSAGE都是非常重要的模型，也是经典baselines
模型的学习要总结出共性，统一的框架，同时比较不同发现创新点

代码复现

开源代码和数据集：
https://github.com/Diego999/pyGAT

数据集

主要是cora，贴点原版readme：
This directory contains the a selection of the Cora dataset (www.research.whizbang.com/data).

The Cora dataset consists of Machine Learning papers. These papers are classified into one of the following seven classes:
Case_Based
Genetic_Algorithms
Neural_Networks
Probabilistic_Methods
Reinforcement_Learning
Rule_Learning
Theory

cora.cites：引用关系，里面都是存的节点-节点

cora.content：特征，第一个数字是节点ID，中间的数字是独热特征，最后一个label

train.py

主函数

from __future__ import division#使得对整形的除法运行后得到小数1/3=0.333不是0
from __future__ import print_function

import os
import glob
import time
import random
import argparse
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable

from utils import load_data, accuracy
from models import GAT, SpGAT

# Training settings
parser = argparse.ArgumentParser()
#是否禁用CUDA训练
parser.add_argument('--no-cuda', action='store_true', default=False, help='Disables CUDA training.')
#是否在训练过程中使用验证集进行验证
parser.add_argument('--fastmode', action='store_true', default=False, help='Validate during training pass.')
#sparse GAT选项
parser.add_argument('--sparse', action='store_true', default=False, help='GAT with sparse version or not.')
#随机种子
parser.add_argument('--seed', type=int, default=72, help='Random seed.')
#训练的epoch次数
parser.add_argument('--epochs', type=int, default=10000, help='Number of epochs to train.')
#学习率初始值
parser.add_argument('--lr', type=float, default=0.005, help='Initial learning rate.')
#L2 norm的weight_decay
parser.add_argument('--weight_decay', type=float, default=5e-4, help='Weight decay (L2 loss on parameters).')
parser.add_argument('--hidden', type=int, default=8, help='Number of hidden units.')
#注意力头数
parser.add_argument('--nb_heads', type=int, default=8, help='Number of head attentions.')
#dropout率（1-保持概率）
parser.add_argument('--dropout', type=float, default=0.6, help='Dropout rate (1 - keep probability).')
parser.add_argument('--alpha', type=float, default=0.2, help='Alpha for the leaky_relu.')
parser.add_argument('--patience', type=int, default=100, help='Patience')

args = parser.parse_args()
args.cuda = not args.no_cuda and torch.cuda.is_available()

#产生随机种子，以使得结果是确定的
random.seed(args.seed)
np.random.seed(args.seed)
torch.manual_seed(args.seed)
if args.cuda:
    torch.cuda.manual_seed(args.seed)

# Load data在utils.py
#加载数据
#adj:adj样本关系的对称邻接矩阵的稀疏张量
#features：样本特征张量
#labels：样本标签
#idx train：训练集索引列表
#idx_val：验证集索引列表
#idx test：测试集索引列表
adj, features, labels, idx_train, idx_val, idx_test = load_data()

# Model and optimizer
#存模型和优化器
#GAT模型
#nfeat输入单元数，shape[1]表示特征矩阵的维度数（列数）产
#nhid中间层单元数量
#nclass辅出单元数，即样本标签数=样本标签最大值+1
#dropout参数
#nheads多头注意力数量
if args.sparse:
    model = SpGAT(nfeat=features.shape[1], 
                nhid=args.hidden, 
                nclass=int(labels.max()) + 1, 
                dropout=args.dropout, 
                nheads=args.nb_heads, 
                alpha=args.alpha)
else:
    model = GAT(nfeat=features.shape[1], 
                nhid=args.hidden, 
                nclass=int(labels.max()) + 1, 
                dropout=args.dropout, 
                nheads=args.nb_heads, 
                alpha=args.alpha)

#构造一个优化器对象Optimizer，用来保存当前的状态，并能够根据计算得到的梯度来更新参数
#Adam优化器
#1r学习率
#weight_decay权重衰减（L2正则）
optimizer = optim.Adam(model.parameters(), 
                       lr=args.lr, 
                       weight_decay=args.weight_decay)

# 是否使用GPU
if args.cuda:
    model.cuda()
    features = features.cuda()
    adj = adj.cuda()
    labels = labels.cuda()
    idx_train = idx_train.cuda()
    idx_val = idx_val.cuda()
    idx_test = idx_test.cuda()

features, adj, labels = Variable(features), Variable(adj), Variable(labels)


def train(epoch):
    t = time.time()#记录时间
    
    #train的时候使用dropout，测试的时候不使用dropout
    #pytorch里面eva1()固定整个网络参数，没有dropout
    
    #训练模型，启用BatchNormalization和Dropout
    model.train()
    
    #把梯度置零，也就是把10ss关于weight的导数变成0
    optimizer.zero_grad()
    #执行GAT中的forward前向传播
    output = model(features, adj)
    #最大似然1og似然损失函数，idx_train是140(从0到139)
    #nll loss:negative log likelihood loss
    #https://www.cnblogs.com/marsggbo/p/10401215.html
    #https://blog.csdn.net/weixin_40476348/article/details/94562240
    loss_train = F.nll_loss(output[idx_train], labels[idx_train])#实际上是交叉熵
    #准确率
    acc_train = accuracy(output[idx_train], labels[idx_train])
    loss_train.backward()
    optimizer.step()#梯度下降

    if not args.fastmode:
        # Evaluate validation set performance separately,
        # deactivates dropout during validation run.
        #测试模型，不启用BatchNormalization和Dropout
        model.eval()
        #前向传播
        output = model(features, adj)

    loss_val = F.nll_loss(output[idx_val], labels[idx_val])
    acc_val = accuracy(output[idx_val], labels[idx_val])
    
    #正在迭代的epoch数
    #训练集损失函数值
    #训练集准确率
    #验证集损失函数值
    #验证集准确率
    #运行时间
    print('Epoch: {:04d}'.format(epoch+1),
          'loss_train: {:.4f}'.format(loss_train.data.item()),
          'acc_train: {:.4f}'.format(acc_train.data.item()),
          'loss_val: {:.4f}'.format(loss_val.data.item()),
          'acc_val: {:.4f}'.format(acc_val.data.item()),
          'time: {:.4f}s'.format(time.time() - t))

    return loss_val.data.item()

#定义测试函数，相当于对已有的模型在测试集上运行对应的loss与accuracy
def compute_test():#测试模型
    model.eval()
    output = model(features, adj)
   # idx_test是1000个（500-1499）
    loss_test = F.nll_loss(output[idx_test], labels[idx_test])
    acc_test = accuracy(output[idx_test], labels[idx_test])
    # print("Test set results:",
    #       "loss= {:.4f}".format(loss_test.data[0]),
    #       "accuracy= {:.4f}".format(acc_test.data[0]))
    print("Test set results:",
      "loss= {:.4f}".format(loss_test.data),
      "accuracy= {:.4f}".format(acc_test.data))


# Train model
t_total = time.time()
loss_values = []
bad_counter = 0
best = args.epochs + 1
best_epoch = 0
for epoch in range(args.epochs):
    loss_values.append(train(epoch))

    torch.save(model.state_dict(), '{}.pkl'.format(epoch))#保存模型参数
    if loss_values[-1] < best:
        best = loss_values[-1]
        best_epoch = epoch
        bad_counter = 0
    else:
        bad_counter += 1

    #连续patience次数效果不变好则提前停止
    if bad_counter == args.patience:
        break

    files = glob.glob('*.pkl')
    for file in files:
        epoch_nb = int(file.split('.')[0])
        if epoch_nb < best_epoch:#保存模型参数的时候如果模型效果不好则跳过
            os.remove(file)

files = glob.glob('*.pkl')
for file in files:
    epoch_nb = int(file.split('.')[0])
    if epoch_nb > best_epoch:
        os.remove(file)

print("Optimization Finished!")
print("Total time elapsed: {:.4f}s".format(time.time() - t_total))

# Restore best model
print('Loading {}th epoch'.format(best_epoch))
model.load_state_dict(torch.load('{}.pkl'.format(best_epoch)))

# Testing
compute_test()

utils.py

主要是加载数据

import numpy as np
import scipy.sparse as sp
import torch


def encode_onehot(labels):
    classes = set(labels)#去掉重复值，得到具体类别
    #identity创建方矩阵
    #字典key为label的值，value为矩阵的每一行，例如有3个类别那么方阵为：
    #1 0 0
    #0 1 0
    #0 0 1
    classes_dict = {c: np.identity(len(classes))[i, :] for i, c in enumerate(classes)}
    #get函数得到字典key对应的value，相当于将labels中每个label对应到方阵的某行独热编码，这里的循环是用map实现的
    #map()会根据提供的函数对指定序列做映射，这里映射的是get函数
    #第一个参数 function 以参数序列中的每一个元素调用 function 函数，返回包含每次 function 函数返回值的新列表，例如：
    #map(lambda x:x**2, [1,2,3,4,5])
    #返回函数x的平方：[1,4.9,16,25]
    
    labels_onehot = np.array(list(map(classes_dict.get, labels)), dtype=np.int32)
    return labels_onehot


def load_data(path="./data/cora/", dataset="cora"):
    """Load citation network dataset (cora only for now)"""
    print('Loading {} dataset...'.format(dataset))

    #content file的每一行的格式为：，是独热编码
    #分别对应0，1：-1，-1
    #feature为第二列到倒数第二列，labe1s为最后一列，具体看笔记的图
    idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset), dtype=np.dtype(str))
    #从第二列到倒数第二列储存为csr型稀疏矩阵
    features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)
    #将每个标签对应到独热编码，这里idx_features_labels是二维数组，逗号前面的冒号代表对第一维所有的数据进行操作，逗号后面的-1代表对最后一列进行操作
    labels = encode_onehot(idx_features_labels[:, -1])

    # build graph
    #cites file的每一行格式为：
    #根据前面的contents与这里的cites创建图，算出edges矩阵与adj矩阵
    
    
    
    #idx_features_labels[:, 0]是将特征中的paperID取出来
    idx = np.array(idx_features_labels[:, 0], dtype=np.int32)
    
    #由于文件中节点并非是按顺序排列的，因此建立一个编号为0-(node_size-1)的哈希表idx_map，
    #哈希表中每一项为old id:number，即节点id对应的编号为number
    #简单的说就是重新按顺序编号
    idx_map = {j: i for i, j in enumerate(idx)}
    
    #edges unordered为直接从边表文件cora.cites中直接读取的edges矩阵结果，是一个(edge_num,2)的数组，每一行表示一条边两个端点的idx
    edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset), dtype=np.int32)
    
    #flatten：降维，返回一维数组
    #边的edges unordered中存储的是节点id，要将每一项的old id换成顺序的新编号。 
    #在idx_map中以idx作为键查找得到对应节点的新编号，reshape成与edges_unordered形状一样的数组（N*2）
    edges = np.array(list(map(idx_map.get, edges_unordered.flatten())), dtype=np.int32).reshape(edges_unordered.shape)
    
    #根据coo矩阵性质，这一段的作用就是，网络有多少条边，邻接矩阵就有多少个1，
    #https://www.cnblogs.com/datasnail/p/11021835.html
    #所以先创建一个长度为edge num的全1数组：(np.ones(edges.shape[0])，每个l的填充位置就是一条边中两个端点的编号：(edges[:, 0], edges[:, 1])
    #即edges[:,0],edges[:,1]，的矩阵形状为（node size，node_size）
    adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])), shape=(labels.shape[0], labels.shape[0]), dtype=np.float32)

    # build symmetric adjacency matrix
    #对于无向图，邻接矩阵是对称的。上一步得到的adj是按有向图构建的，转换成无向图的邻接矩阵需要扩充成对称矩阵
    #将i->j与j->i中权重最大的那个，作为无向图的节点与节点j的边权。
    #https://blog.csdn.net/Eric_1993/artic1e/details/102907104
    adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)

    features = normalize_features(features)
    
    #eye创建单位矩阵，第一个参数为行数，第二个为列数
    #GCN论文中对应：A^=(D~)^0.5A~(D~)^0.5
    #其中：A~=A+I_N
    adj = normalize_adj(adj + sp.eye(adj.shape[0]))

    #划分训练验证测试集
    idx_train = range(140)
    idx_val = range(200, 500)
    idx_test = range(500, 1500)

    #创建特征矩阵、标签向量和邻接矩阵的tensor，用来做模型的输入
    adj = torch.FloatTensor(np.array(adj.todense()))
    features = torch.FloatTensor(np.array(features.todense()))
    labels = torch.LongTensor(np.where(labels)[1])

    idx_train = torch.LongTensor(idx_train)
    idx_val = torch.LongTensor(idx_val)
    idx_test = torch.LongTensor(idx_test)

    return adj, features, labels, idx_train, idx_val, idx_test


def normalize_adj(mx):
    """Row-normalize sparse matrix"""
    #https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780
    #https://towardsdatascience.com/understanding-graph-convolutional-networks-for-node-classification-a2bfdb7aba7b
    #这里的思想是：
    #1.给出邻接矩阵A和特征矩阵X
    #2.将特征矩阵中的值通过相乘的方式换为邻居节点的特征（邻居特征累加）
    #3.为了把自身的影响加入计算，将表示自己的对角线上都置1后计算（A+I_N）
    #4.为了防止邻居节点个数不均造成的不公平，这里对求得的影响要进行normalization，就是除以每个节点的度
    #GCN论文中对应：A^=(D~)^0.5A~(D~)^0.5
    #其中：A~=A+I_N
    
    #对每一行求和    
    rowsum = np.array(mx.sum(1))
    #(D~)^0.5
    r_inv_sqrt = np.power(rowsum, -0.5).flatten()
    #如果某一行全为0，则上一步r_inv算出来的结果会等于无穷大，将这些行的r_inv置为0
    r_inv_sqrt[np.isinf(r_inv_sqrt)] = 0.
    #构建对角元素为r_inv的对角矩阵
    r_mat_inv_sqrt = sp.diags(r_inv_sqrt)
    return mx.dot(r_mat_inv_sqrt).transpose().dot(r_mat_inv_sqrt)


def normalize_features(mx):
    """Row-normalize sparse matrix"""
    #按行求和
    rowsum = np.array(mx.sum(1))
    #求倒数
    r_inv = np.power(rowsum, -1).flatten()
    #如果某一行全为0，则上一步r_inv算出来的结果会等于无穷大，将这些行的r_inv置为0
    r_inv[np.isinf(r_inv)] = 0.
    #构建对角元素为r_inv的对角矩阵
    r_mat_inv = sp.diags(r_inv)
    #用对角矩阵与原始矩阵的点积起到标准化的作用，原始矩阵中每一行元素都会与对应的r_inv相乘，最终相当于除以了sum
    #就是对应的行除以对应的行和
    mx = r_mat_inv.dot(mx)
    return mx


def accuracy(output, labels):
    preds = output.max(1)[1].type_as(labels)
    correct = preds.eq(labels).double()
    correct = correct.sum()
    return correct / len(labels)

models.py

import torch
import torch.nn as nn
import torch.nn.functional as F
from layers import GraphAttentionLayer, SpGraphAttentionLayer


class GAT(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout, alpha, nheads):
        """Dense version of GAT."""
        super(GAT, self).__init__()
        self.dropout = dropout
        
        #在layer.py中定义，第一层卷积多头
        self.attentions = [GraphAttentionLayer(nfeat, nhid, dropout=dropout, alpha=alpha, concat=True) for _ in range(nheads)]
        for i, attention in enumerate(self.attentions):#按多头注意力个数加入attention layer
            self.add_module('attention_{}'.format(i), attention)
                
        #第二层卷积只用一头
        #nhid是每个attention layer的输出维度这里用的是8，然后有8个头，输出concat后变成8*8维
        self.out_att = GraphAttentionLayer(nhid * nheads, nclass, dropout=dropout, alpha=alpha, concat=False)

    def forward(self, x, adj):
        x = F.dropout(x, self.dropout, training=self.training)
        x = torch.cat([att(x, adj) for att in self.attentions], dim=1)#相对应原文公式5，多头注意力结果拼接，这里维度是多头数量*output维度，这里是64
        x = F.dropout(x, self.dropout, training=self.training)
        x = F.elu(self.out_att(x, adj))#将64降维到output维度
        return F.log_softmax(x, dim=1)#返回：按行进行softmax得到没行是每个分类的概率，然后再去log

#这个貌似是一个特别版本，不展开原网站有说明
class SpGAT(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout, alpha, nheads):
        """Sparse version of GAT."""
        super(SpGAT, self).__init__()
        self.dropout = dropout

        self.attentions = [SpGraphAttentionLayer(nfeat, 
                                                 nhid, 
                                                 dropout=dropout, 
                                                 alpha=alpha, 
                                                 concat=True) for _ in range(nheads)]
        for i, attention in enumerate(self.attentions):
            self.add_module('attention_{}'.format(i), attention)

        self.out_att = SpGraphAttentionLayer(nhid * nheads, 
                                             nclass, 
                                             dropout=dropout, 
                                             alpha=alpha, 
                                             concat=False)

    def forward(self, x, adj):
        x = F.dropout(x, self.dropout, training=self.training)
        x = torch.cat([att(x, adj) for att in self.attentions], dim=1)
        x = F.dropout(x, self.dropout, training=self.training)
        x = F.elu(self.out_att(x, adj))
        return F.log_softmax(x, dim=1)

layers.py

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F


class GraphAttentionLayer(nn.Module):
    """
    Simple GAT layer, similar to https://arxiv.org/abs/1710.10903
    """
    def __init__(self, in_features, out_features, dropout, alpha, concat=True):
        super(GraphAttentionLayer, self).__init__()
        self.dropout = dropout
        self.in_features = in_features#读入维度
        self.out_features = out_features#输出维度，这里是8
        self.alpha = alpha#学习因子
        self.concat = concat

        #建立都是0的矩阵，大小为（输入维度，输出维度）
        self.W = nn.Parameter(torch.empty(size=(in_features, out_features)))
        nn.init.xavier_uniform_(self.W.data, gain=1.414)#xavier初始化
        self.a = nn.Parameter(torch.empty(size=(2*out_features, 1)))#这里的self.a，对应的是论文里的向量a，故其维度大小应该为(2*out_features，1)
        nn.init.xavier_uniform_(self.a.data, gain=1.414)

        self.leakyrelu = nn.LeakyReLU(self.alpha)

    def forward(self, h, adj):
        Wh = torch.mm(h, self.W) # h.shape: (N, in_features), Wh.shape: (N, out_features),这里N=2708，out_features=8（labe1的个数）
        #相对于原文公式3分子中hi和hj拼接那部分
        a_input = self._prepare_attentional_mechanism_input(Wh)
        #即论文星的eij
        #squeeze去掉第2个维度
        #[2708,2708,16]与[16,1]相乘得到[2708,2708,1]再去掉维数为1的维度，故其维度为[2708,2708]，与领接矩阵adj的维度一样
        e = self.leakyrelu(torch.matmul(a_input, self.a).squeeze(2))

        #上面得到是当前点和所有点的attention权重，但是我们只关心邻居节点，所以这里有一个mask attention操作。
        
        #维度大小与e相同[2708,2708]，所有元素都是-9*10的15次方，取一个很小的值，经过softmax后就变成0
        zero_vec = -9e15*torch.ones_like(e)
        
        #邻接矩阵adj维度为[2708,2708]（归一化处理之后的）
        #当adj中的值>0，即两个节点有边，则用e这个算出来的attention权重，如果没有边则设置为zero_vec
        attention = torch.where(adj > 0, e, zero_vec)
        #相对应原文公式3计算softmax
        attention = F.softmax(attention, dim=1)
        attention = F.dropout(attention, self.dropout, training=self.training)#抓爆
        h_prime = torch.matmul(attention, Wh)#相对应原文公式4，下面加elu

        if self.concat:
            return F.elu(h_prime)
        else:
            return h_prime

    def _prepare_attentional_mechanism_input(self, Wh):
        N = Wh.size()[0] # number of nodes

        # Below, two matrices are created that contain embeddings in their rows in different orders.
        # (e stands for embedding)
        # These are the rows of the first matrix (Wh_repeated_in_chunks): 
        # e1, e1, ..., e1,            e2, e2, ..., e2,            ..., eN, eN, ..., eN
        # '-------------' -> N times  '-------------' -> N times       '-------------' -> N times
        # 
        # These are the rows of the second matrix (Wh_repeated_alternating): 
        # e1, e2, ..., eN, e1, e2, ..., eN, ..., e1, e2, ..., eN 
        # '----------------------------------------------------' -> N times
        # https://www.jianshu.com/p/a2102492293a
        
        Wh_repeated_in_chunks = Wh.repeat_interleave(N, dim=0)#下面左边这列
        Wh_repeated_alternating = Wh.repeat(N, 1)#下面右边这列
        # Wh_repeated_in_chunks.shape == Wh_repeated_alternating.shape == (N * N, out_features)

        # The all_combination_matrix, created below, will look like this (|| denotes concatenation):
        # e1 || e1
        # e1 || e2
        # e1 || e3
        # ...
        # e1 || eN
        # e2 || e1
        # e2 || e2
        # e2 || e3
        # ...
        # e2 || eN
        # ...
        # eN || e1
        # eN || e2
        # eN || e3
        # ...
        # eN || eN
        #实际是相对于穷举了所有节点两两相互之间的组合

        #得到上面的组合矩阵，它有N*N种两两组合，因此有N*N行，每个e的维度是out_features=8
        #两个拼接后是2*8，因此整体维度是：(N*N,2*out_features)
        all_combinations_matrix = torch.cat([Wh_repeated_in_chunks, Wh_repeated_alternating], dim=1)
        # all_combinations_matrix.shape == (N * N, 2 * out_features)

        #再变成tensor
        return all_combinations_matrix.view(N, N, 2 * self.out_features)

    def __repr__(self):
        return self.__class__.__name__ + ' (' + str(self.in_features) + ' -> ' + str(self.out_features) + ')'


class SpecialSpmmFunction(torch.autograd.Function):
    """Special function for only sparse region backpropataion layer."""
    @staticmethod
    def forward(ctx, indices, values, shape, b):
        assert indices.requires_grad == False
        a = torch.sparse_coo_tensor(indices, values, shape)
        ctx.save_for_backward(a, b)
        ctx.N = shape[0]
        return torch.matmul(a, b)

    @staticmethod
    def backward(ctx, grad_output):
        a, b = ctx.saved_tensors
        grad_values = grad_b = None
        if ctx.needs_input_grad[1]:
            grad_a_dense = grad_output.matmul(b.t())
            edge_idx = a._indices()[0, :] * ctx.N + a._indices()[1, :]
            grad_values = grad_a_dense.view(-1)[edge_idx]
        if ctx.needs_input_grad[3]:
            grad_b = a.t().matmul(grad_output)
        return None, grad_values, None, grad_b


class SpecialSpmm(nn.Module):
    def forward(self, indices, values, shape, b):
        return SpecialSpmmFunction.apply(indices, values, shape, b)

    
class SpGraphAttentionLayer(nn.Module):
    """
    Sparse version GAT layer, similar to https://arxiv.org/abs/1710.10903
    """

    def __init__(self, in_features, out_features, dropout, alpha, concat=True):
        super(SpGraphAttentionLayer, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.alpha = alpha
        self.concat = concat

        self.W = nn.Parameter(torch.zeros(size=(in_features, out_features)))
        nn.init.xavier_normal_(self.W.data, gain=1.414)
                
        self.a = nn.Parameter(torch.zeros(size=(1, 2*out_features)))
        nn.init.xavier_normal_(self.a.data, gain=1.414)

        self.dropout = nn.Dropout(dropout)
        self.leakyrelu = nn.LeakyReLU(self.alpha)
        self.special_spmm = SpecialSpmm()

    def forward(self, input, adj):
        dv = 'cuda' if input.is_cuda else 'cpu'

        N = input.size()[0]
        edge = adj.nonzero().t()

        h = torch.mm(input, self.W)
        # h: N x out
        assert not torch.isnan(h).any()

        # Self-attention on the nodes - Shared attention mechanism
        edge_h = torch.cat((h[edge[0, :], :], h[edge[1, :], :]), dim=1).t()
        # edge: 2*D x E

        edge_e = torch.exp(-self.leakyrelu(self.a.mm(edge_h).squeeze()))
        assert not torch.isnan(edge_e).any()
        # edge_e: E

        e_rowsum = self.special_spmm(edge, edge_e, torch.Size([N, N]), torch.ones(size=(N,1), device=dv))
        # e_rowsum: N x 1

        edge_e = self.dropout(edge_e)
        # edge_e: E

        h_prime = self.special_spmm(edge, edge_e, torch.Size([N, N]), h)
        assert not torch.isnan(h_prime).any()
        # h_prime: N x out
        
        h_prime = h_prime.div(e_rowsum)
        # h_prime: N x out
        assert not torch.isnan(h_prime).any()

        if self.concat:
            # if this layer is not last layer,
            return F.elu(h_prime)
        else:
            # if this layer is last layer,
            return h_prime

    def __repr__(self):
        return self.__class__.__name__ + ' (' + str(self.in_features) + ' -> ' + str(self.out_features) + ')'