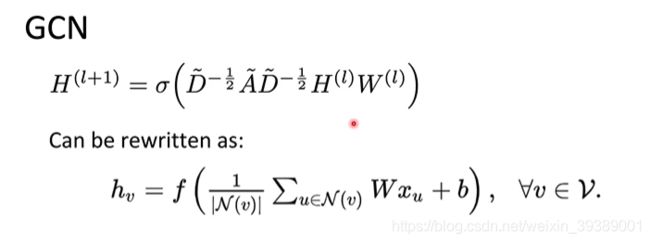Graph Neural Network学习笔记-Day2

参考清单如下：
B站视频

知乎Johnny Richards

知乎Taylor Wu

接上一篇blog：Graph Neural Network学习笔记-Day1

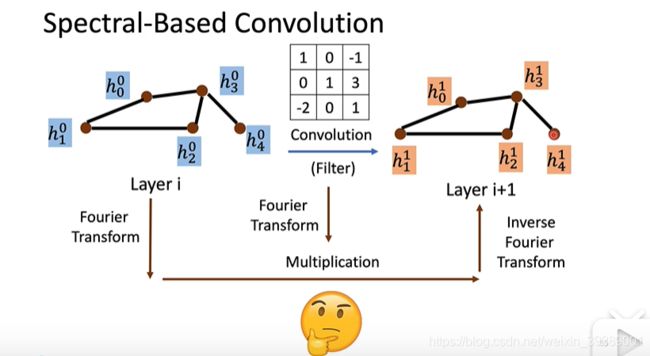
Spectral-Based Convolution

和Spatial-based convolution不同，Spectral-Based Convolution就是根据“时域卷积<==>频域乘积”的性质，通过傅里叶变换，把时域需要卷积的feature和卷积核，变换到频域，相乘之后再傅里叶反变换过去，从而完成卷积。

基础知识☞Spectral Graph Theory

主要是理解graph如何变换到谱域，如何进行傅里叶变换

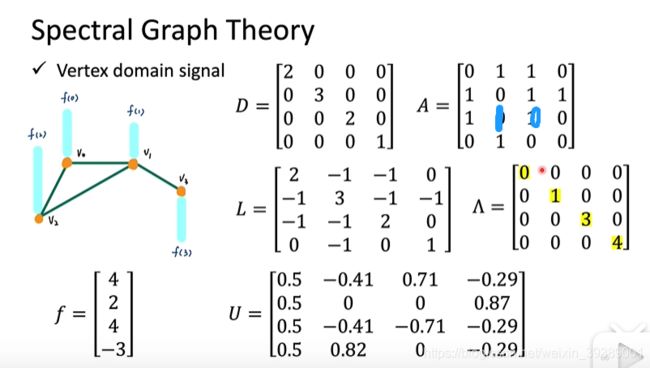
基本概念

• 什么是graph（包括节点，边，节点个数是N）
• ajacency matrix（节点与节点之间有边则对应位置的矩阵元素为1，否则为0。是对称矩阵）
• 只考虑无向图
• degree matrix（是对角矩阵，对角线元素就是节点的度
• 信号（节点上的一个函数）
  如下图所示，一个demo graph和它上面的信号（如每个节点表示城市，那么信号可以是该城市的气温、人口增长数，等）
  

拉普拉斯算子

• graph的拉普拉斯矩阵L=D-A
• L是对称的
• L进行谱分解 $L=U\Lambda U^T$
• $\Lambda =diag[{\lambda }_0,\cdots ,{\lambda }_{N-1}]$对角矩阵，元素是L的特征值
• U 酉矩阵，$U=[u_0,\cdots ,u_{N-1}]$，列向量是L的特征值对应的特征向量。是一组标准正交基（自己和自己的内积是1，两两之间内积为0）。
• ${\lambda }_l$就是谱域的频率，基向量$u_l$就是频率${\lambda }_l$对应的基向量。

对于demo graph，给出上面的信号$f$。根据graph的样子，可以得到D，A，L，以及L谱分解之后的$\Lambda$,$U$。

怎么理解特征值是频率

$\lambda =0$就是直流分量，特征向量$u_0$这四个节点上的信号强度相同，${\lambda }_i$越大，特征向量在节点上变化的就越快。

还是以上面的demo graph为例子，考察拉普拉斯算子究竟干了什么~~

如上图所示，L算子作用到graph的信号$f$上面$Lf=(D-A)f=Df-Af$，只考察第一个节点$v_0$, 第一个节点变换后的值$a = D(1,:) f - A(1,:)f $，其中$D(1,:)$,$A(1,:)$ 分别表示这两个矩阵的第一行。那么就是$v_0$上的signal$f(1)$乘以节点的度，然后减去与$v_0$相邻的节点的信号。如上图，整理成 $v_0$上的信号和它的邻居节点的信号之差，再求和。所以这就是信号强度的变化。如果考虑功率的话，就用$f^{T}Lf$，如下图所示，整理成了相邻node之间信号功率的变化，或者是graph上信号平滑程度。平滑程度就是频率，频率越高，相邻信号之间能量差就越大，频率越低，相邻信号之间的能量差就越小。

把信号用特征向量替代，有

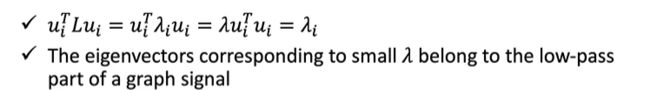
所以特征值就是特征向量的频率大小。

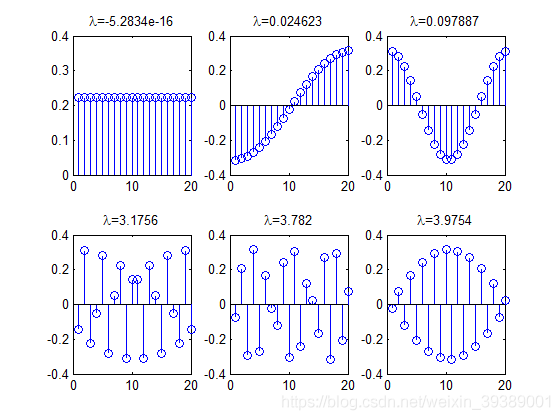
例如下图中的demo graph，是一个具有20个node的 line graph。根据这个graph的L进行谱分解，得到的$\lambda$和对应的$u$如下面六张图，其中$\lambda$越大，节点之间信号变化就越快。

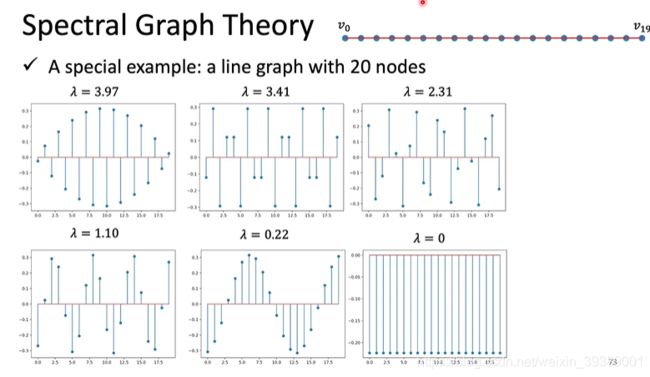
自己随便画了一下

关于拉普拉斯啰嗦点别的

参考知乎上一篇回答，感觉挺有趣。

从热传播模型到图上的信号传播模型

热传播模型

顾名思义就是热量是怎么传播的咯。
牛顿冷却定律（Newton’s Law of Cooling)说，当物体表面与周围存在温度差时，单位时间从单位面积散失的热量与温度差成正比，比例系数称为热传递系数（摘自：百度百科）。假设这个比例系数为$k$，在一维、离散假设下，位于$i$处的一个点的温度为${\varphi }_i$,那么${\varphi }_i$变化快慢$\frac{d{\varphi }_i}{dt}$就是其周围相邻的两个点$i-1$和$i+1$的温度${\varphi }_{i-1}$和${\varphi }_{i+1}$分别与${\varphi }_i$的差乘以比例系数$k$。即
$\frac{d{\varphi }_i}{dt}=k({\varphi }_{i+1}-{\varphi }_i)-k({\varphi }_i-{\varphi }_{i-1})$
这里假设点$i$从$i+1$处接收热量，向$i-1$处传播热量。这么表示是为了后面写成二阶导数的形式。。。其他情况也可以转化成该形式。
不难看出，等式右边其实是温度对空间位置的二阶偏导数，即
$\frac{d{\varphi }_i}{dt}=k[({\varphi }_{i+1}-{\varphi }_i)-({\varphi }_i-{\varphi }_{i-1})]=k\frac{{\partial }^2{\varphi }_i}{\partial x^2}$
因此，一维连续空间的热传导方程就可以写为：
$\frac{d\varphi }{dt}-k\frac{{\partial }^2\varphi }{\partial x^2}=0.$
上面是一维的情况，对于高维情况下，等式右边的二阶偏导数就变成了拉普拉斯算子${▽}^2$。
$\frac{d\varphi }{dt}-k{▽}^2\varphi =0.$

拉普拉斯算子就是梯度的散度，是一个二阶微分算子，是笛卡尔坐标系$x_i$中的所有非混合二阶偏导数：${\sum }_{i=1}^n\frac{{\partial }^2}{\partial x_i^2}$

图的热传播模型（也可以是各种别的信号）

一个Graph可以表示为节点V和边E的集合。用邻接矩阵A（Ajacency Matrix）来表示各个节点之间的连接关系。$a_{ij}=1$表示$v_i$和$v_j$之间是相连的；$a_{ij}=0$则表示$v_i$和$v_j$之间没有边。假设热量在图的节点与节点之间传播，那么只有在相邻的节点之间才有传播，因此
$\frac{d{\varphi }_{v_i}}{dt}=k{\sum }_{j=1}^N{a}_{ij}({\varphi }_{v_i}-{\varphi }_{v_j})$
其中$N$表示Graph中的节点总数。上式中，对于A中的第$i$行，只把其中为1（与$v_i$相连接）对应的节点与节点$v_i$的温度差取出，乘以热传递的比例系数k。
把上面式子稍作整理：
$\frac{d{\varphi }_{v_i}}{dt}=k({\varphi }_{v_i}{\sum }_{j=1}^N{a}_{ij}-{\sum }_{j=1}^N{a}_{ij}{\varphi }_{v_j})=k({\varphi }_{v_i}{d}_i-{\sum }_{j=1}^N{a}_{ij}{\varphi }_{v_j})$
其中$d_i$表示节点$v_i$的度。
把所有节点都考虑进来表示成列矩阵$\varphi =[\frac{d{\varphi }_{v_1}}{dt},\dots ,\frac{d{\varphi }_{v_N}}{dt}{]}^T$，令D为对角矩阵，对角线元素就是节点的度，则
$\frac{d\varphi }{dt}=k(D\varphi -A\varphi )=k(D-A)\varphi$
其中$D-A$就是拉普拉斯矩阵$L$，所以有
$\frac{d\varphi }{dt}-kL\varphi =0$
是不是和上面的红色公式一毛一样？？—区别只是一个是欧式空间、一个是拓扑空间哟。

$\frac{d\varphi }{dt}=kL\varphi$ 这个公式可以这样解释哦，对一个graph上用L算子作用到每个节点的温度上是有什么意义呢？忽略这个常数k的话，L作用到$\varphi$得到的就是节点的温度变换率。

L的特征函数

欧式空间上，L的特征函数是$e^{-j\omega t}$，因为易知
$L{e}^{-j\omega t}=-{\omega }^2{e}^{-j\omega t}$
欧式空间中，基函数（特征函数）有无穷多个
在graph里面，L是N维的，N是graph的节点数。所以特征空间是有限维的。
上面也很容易看出，特征向量对应的是和频率相关的。

傅里叶变换和拉普拉斯算子的关系

一开始我们就说，spectral-based GNN是把graph和卷积核都进行傅里叶变换，在谱域相乘之后，反变换回来。那么为什么讲了半天L还没出现傅里叶变换呢？下面就是傅里叶变换了。

傅里叶变换就是信号在一组基函数上的展开，这组基函数就是拉普拉斯算子的特征函数。

相应的，推广到graph上，就是把graph的信号在一组基向量上展开，用的就graph的拉普拉斯算子的特征向量$U$。
所以graph的傅里叶变换就是
$F=U^{T}f$ 这里积分变成了向量的内积。意义都是一样的，都是原来的信号f在基函数$e^{-j\omega t}$ 或者基向量$u_i$是上面的投影。

下图解释的就是上面的graph的傅里叶变换。其中，内积的值对应的就是不同频率${\lambda }_0$,${\lambda }_1$,${\lambda }_2$,${\lambda }_3$上面的信号分量的大小。

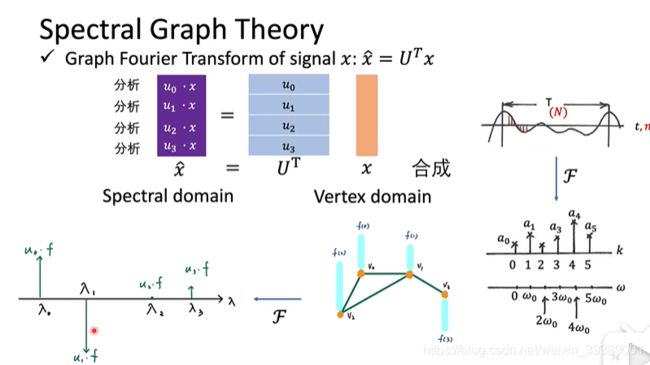
这样我们就有了graph Fourier Transform的方法。
逆傅里叶变换更简单，就是

因为$U{U}^T=I$ 所以就变回了原来的$x$。当然也可以对应传统的逆傅里叶变换，从物理意义上去解释。

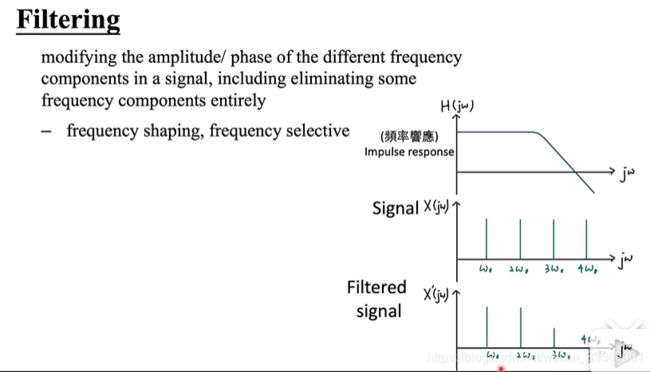
怎样把Graph傅里叶变换到频域做卷积

卷积就相当于信号经过了一些线性系统，或者叫做滤波器。时域上是卷积，频域就是滤波器的频率响应和信号的频率相乘。把某一些频率的信号放大了，某一些频率的信号抑制了。如下图所示。

graph的滤波
如下图，也是graph的信号的spectral domain $\hat{x}$，和一个滤波器$g_{\theta }(\Lambda )$相乘。滤波器的参数$\theta$是待训练的参数，滤波器的自变量$\Lambda$就是L的特征值，因为滤波器是在不同的特征值（频率）上的响应。比如$\theta$可以定义为就是每个频率${\lambda }_i$上面的滤波器响应值${\theta }_i$。

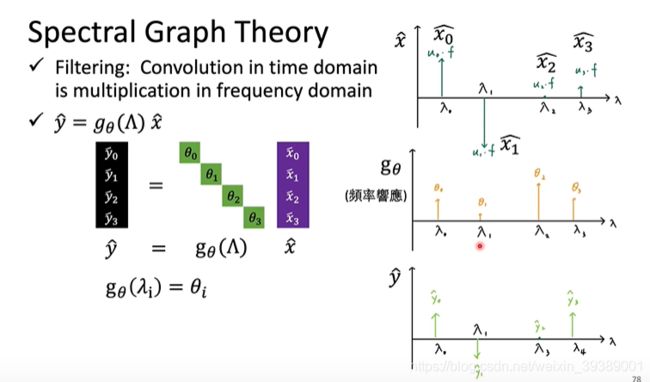
这样就在频域完成了滤波。最后反变换回去就可以了。也就是下图所示。

整理一下，整个傅里叶变换，滤波，反变换过程，就是下图所示。其中把关于特征值的函数$g_{\theta }$提到外面，就变成了$y=g_{\theta }(L)x$

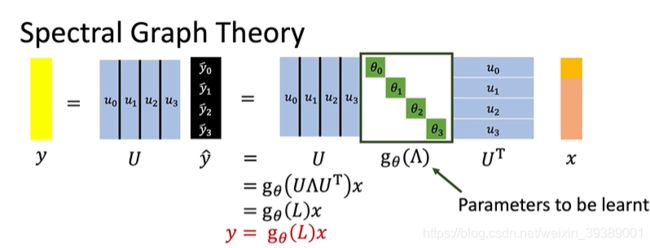
对一个graph进行卷积，就是定义一个$g_{\theta }(L)$。
终于，卷积完成啦！！！

卷积函数的讨论

如果按照下面的定义来构造graph convolution，很显然卷积核大小和graph的大小有关，是个问题。

另外，L的几次方其实代表着对graph的卷积感受野的大小，L就是只考虑和node一步相邻的node，$L^k$就表示k步相邻的node都考虑进去，$L^N$就是整个graph的全局特征了。对于某些数据集来讲，可能需要局部特征更好一些。

也就是这里面说的第一代卷积核以及存在的问题

ChebNet

选用的$g_{\theta }(L)$是L的多项式加权和，权重是要学习的参数$\theta$，只考虑L的前K次方。但是因为还是要计算U矩阵的乘法，所以时间复杂度依然很高。

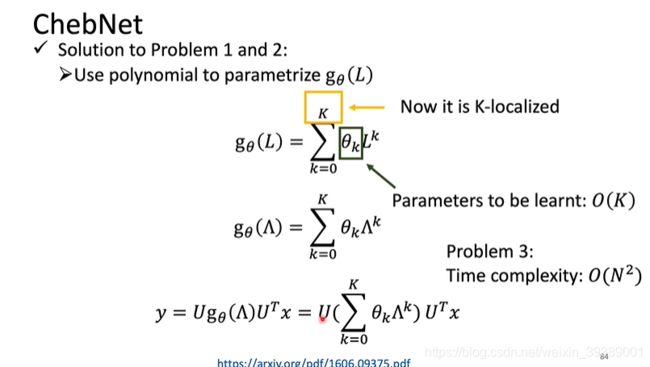
为了解决上述问题，采用下面的Chebyshev多项式函数。可以递归计算~~

根据Chebyshev多项式函数，把本来定义的关于$\Lambda$的多项式函数替换成了Chebyshev多项式函数

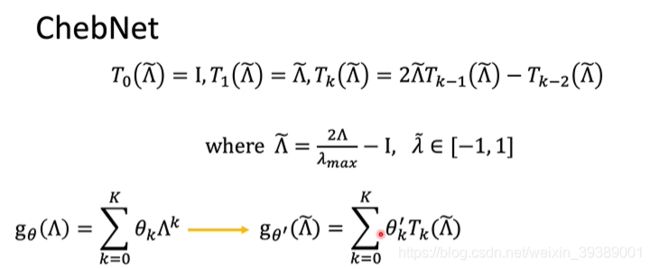
可以用递归的方式来把${\bar{x}}_0...{\bar{x}}_K$求好，然后和待学习的参数${\theta }^{\prime }$相乘就得到了卷积输出。从而解决了要求N阶矩阵乘法的问题。
详细的过程点这个知乎
对应其中的第二代GCN

GCN

ChebNet取K=1就是下面的了。


是现有最成熟的第三代GCN方法