【Transformer】李沐论文逐段精读学习笔记

参考

摘要

贡献：网络简单，且跟之前的网络结构都不一样，不使用rnn或cnn的单元。并行度更好，训练快很多。在机器翻译上取得了更好的效果。

结论

本文提出的Transformer是第一个纯基于attention的序列转录模型，使用multi-head self-attention替代了之前的rnn结构。

在机器翻译上，比RNN和CNN都要快，还取得了新的SOTA。

Intro（导言）

• 介绍了传统的RNN，CNN以及encoder-decoder架构。

• 分析了RNN的缺点：

  1. 难以并行。

  2. 容易遗忘。

• 再介绍了attention机制。最后提出了一个全新的架构Transformer。

Background（相关工作）

为了提高对序列数据的计算效率，很多工作都使用卷积神经网络作为基础的building block来进行模型构建，从而实现并行的计算。然而，CNN是通过滑动窗口来提取特征，所以对于长距离的关系较难捕捉。但CNN还有一个优点——多通道机制，使得模型可以从多个角度去提取数据的特征。

所以Transformer借用了多通道的思想，设计了多头的注意力机制。

另外，self-attention不是本工作提出了，而是在曾经的很多工作中都被成功应用了。

模型

序列模型中较好的是encoder-decoder架构。

要点：

1. encoder把输入序列处理得到中间表示，然后decoder读入这个中间表示，处理后得到输出序列；

2. 输入序列和输出序列不一定一样长；

3. decoder是一种auto-regressive的方式来输出的，即每一步都会读入上一步的输出。

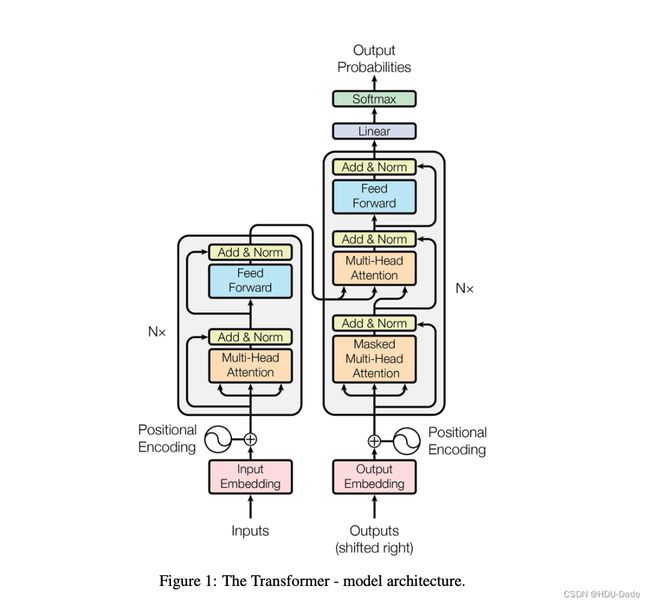
Transformer依然是一个encoder-decoder的架构，但它主要组成是self-attention和point-wise fully connected layer，结构如下：

李沐: 这个图画的很好，在神经网络的时代，画图是一个重要的技能。然而这个图属于那种“不明觉厉”的图，很好看，但是不容易看懂。

Encoder

• Encoder由N=6个一模一样的层组成；

• 每个层，包含2个子层：①multi-head self-attention layer，②position-wise fully connected feed-forward network （就是个MLP）；

• 每个子层，都会使用residual connection和layer norm来处理，子层的输出都可以表示为：
  $$LayerNorm(x+Sublayer(X))$$

为了方便残差连接，上面所有的层、包括embedding层，都使用d=512作为输出维度。

总之，Encoder就俩超参数：N和d。这种设计直接影响了后面各种基于Transformer的模型设计，比如BERT，GPT等等，都主要调节这两个参数。

Layer Norm

• Batch Norm就是把一个batch的tensor，按照feature的每个维度（即按照列）去进行规范化（均值0方差1）

• Layer Norm则是在batch内逐个样本去做规范化
  

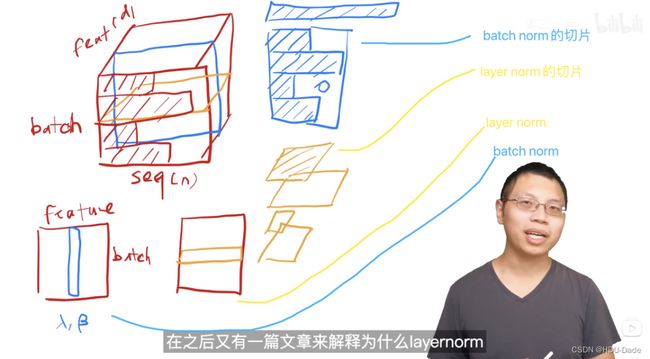
我们在序列化数据中更常使用的是Layer Norm

因为序列的长度会变化，如果使用batch norm的话，可能导致均值方差波动很大，从而影响效果，而layer norm则是逐个样本去进行的，就不会受影响。

Decoder

• 跟Encoder一样由N=6个一模一样的层构成；

• 每个层，包含3个子层，相比于Encoder中的设计，多了一个multi-head attention layer；

• 为了防止Decoder在处理时看到未来的信息，这里对self-attention做了进一步的处理，即使用了一个mask机制，在t时刻时把后面的单元都mask掉，从而不会attend到未来的信息。

逐个看看每个sub-layer：

Scaled Dot-product Attention

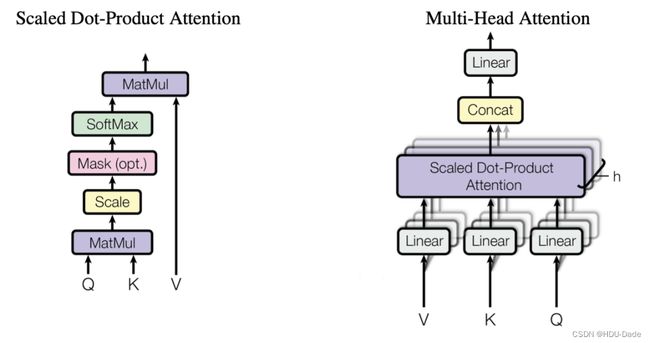
在Transformer中我们使用的attention机制是Scaled Dot-product Attention，下图中的

$$d_k$$
代表的Q，K，V的维度：

这里的attention机制，相比于经典的Dot-product Attention其实就是多了一个scale项。

除以$d_k$为了防止softmax函数的梯度消失。
当d比较小的时候，要不要scale都无所谓，
但是当d比较大时，内积的值的范围就会变得很大，不同的内积的差距也会拉大，
这样的话，再经过softmax进一步的扩大差距，就会使得得到的attention分布很接近one-hot。值就会更加向两端靠拢，算梯度的时候，梯度比较小。
softmax会让大的数据更大，小的更小。这样会导致梯度下降困难，模型难以训练。
在Transformer中，d=512，算比较大了，因此需要进行scaling。

Multi-Head Attention

原本的SDP Attention，没什么可学习的参数，作者发现，我们可以先把原本的向量，通过线性层隐射到多个低维的空间，然后再并行地进行SDP Attention操作，在concat起来，可以取得更好的效果。这类似于CNN中的多通道机制。一个向量先隐射成多个更低维的向量，相当于分成了多个视角，然后每个视角都去进行Attention，这样模型的学习能力和潜力就会大大提升，另外由于这里的降维都是参数化的，所以让模型可以根据数据来学习最有用的视角。

进入一个线形层，线形层把 value、key、query 投影到比较低的维度。然后再做一个 scaled dot product ，执行 h 次会得到 h 个输出，再把 h 个 输出向量全部合并 concat 在一起，最后做一次线性的投影 Linear，会回到我们的 multi-head attention。

每一个head是把QKV通过可以学习的矩阵Wq, Wk, Wv 投影到 dv上，再通过注意力函数，得到 head的结果。

Point-wise Feed-forward Networks

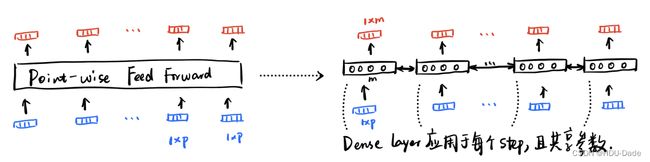
实际上就是简单的MLP。唯一需要注意的是这个MLP的修饰词——Point-wise，它的意思是它是对每个position（词）都分开、独立地处理。

MLP只是作用于最后一个维度，具体公式是：
$$FFN(x)=relu(x{W}_1+b_1)W_2+b_2$$

FFN： Linear + ReLU + Linear

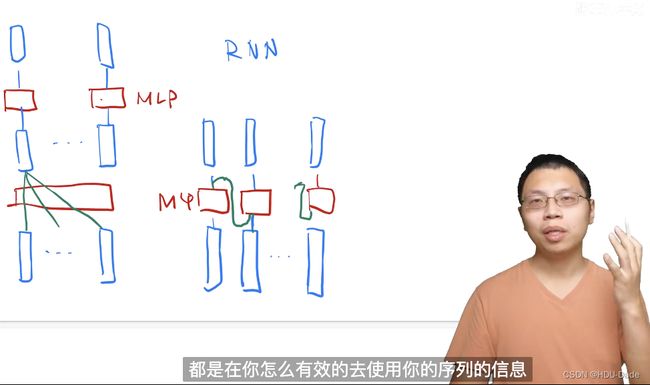
左边是Transformer示意图，右边是RNN示意图（其中对RNN单元简化成一个MLP，本质上类似）。

• Transformer是通过attention来全局地聚合序列的信息，然后通过MLP进行语义空间的转换；

• RNN则是通过把上一时刻的信息传入下一时刻的单元，来使用序列信息，但也是通过MLP进行语义空间转换。所以二者本质区别在于如何使用序列的信息。

Embedding和softmax层

Transformer中使用了三处embedding：
对input和output的token进行embedding，
以及在softmax前面的Linear transformation中也使用跟embedding相同的权重
（这样是为了能够把decoder的output通过相同的embedding给转换回token的概率，因为embedding的作用就是做token跟vector之间的转换）。
三处的embedding都是同样的权重。

为了让训练更简单。

另外值得注意的点就是，作者把embedding都乘上了

$$\sqrt{d_{model}}$$

为了在后面跟position embedding相乘的时候能够保持差不多的scale。

Position Encoding

由于self-attention实际上是不考虑序列顺序的，只是单纯把各个position的信息进行聚合，无论顺序怎么改变，对于self-attention来说都是一样的。因此，这里特意设计了position encoding这种东西，来添加位置信息。

具体的，文章使用的是周期不同的sin和cos函数来计算得到每个position的Embedding：

$$PE(pos,2i)=sin(pos/10000^{2i/d_{model}})$$
$$PE(pos,2i+1)=cos(pos/10000^{2i/d_{model}})$$

其中pos是具体位置的index，i则是具体的dimension。总之，这里给每个位置，都构造了一个长为

$$d_{model}=512$$
的向量，来作为该position也就是某个具体token的位置表示。

最后，这个position encoding是直接跟embedding相加，输入到模型中。

为什么使用Self-Attention

整个文章实际上对模型的解释是比较欠缺的。

作者主要通过下面这个表来对比self-attention和其他结构的差别（restricted self-attention不用管，不怎么用）：

sequential operations衡量的是在处理序列的时候的并行复杂度，越小说明并行度越高；

max path length则表示序列中任意两个点传递信息的最大距离。

Self-attention的主要优势在于并行度高（相比RNN）、信息距离短（相比RNN和CNN）。
而在复杂度方面，其实没有明显优势：

• self-attention每层的复杂度是
  $$O(n^2\cdot d)$$
  是因为有n个position，每个position都要计算n次attention，在计算attention的时候，是进行维度为d的内积，所以复杂度是n * n * d；

• RNN层的复杂度是
  $$O(n\cdot d^2)$$
  因为有n个position，每个position会经过一个线性变化（矩阵乘法），变换的复杂度是d * d，因此最终复杂度是n * d * d；

• CNN实际上跟RNN类似，但因为往往涉及到多个kernel，所以多乘了一个k。
  $$O(k\cdot n\cdot d^2)$$
  但一般在NLP中k也不大，所以没有大差别。

在NLP中，往往n和d都会比较大，所以这三者的计算复杂度没有质的差别。

看起来应该Transformer在计算效率上会比CNN、RNN更快，但我们现在体会到的Transformer的模型却不是这样的，为啥呢？实际上是因为self-attention对整个模型的假设更少，所以我们往往需要更大量的数量、更大的模型才能够训练出跟CNN、RNN同样的效果来。这就导致现在基于Transformer的模型都特别大特别贵。

训练细节&超参数

英语翻译德语，使用BPE分词法构造英语德语共用的词典，使用8个P100 GPU，每个batch大概0.4s，总共训练了12小时，其实时间成本相对来说还是可承受的。

学习率使用了warmup，先增强后减。

使用了两种正则化：

• Residual dropout，对每个sub-layer的输出都使用了dropout，还对embedding层也使用dropout，dropout rate=0.1

• Label Smoothing，使用了程度为0.1的smoothing，这会损害一点的perplexity，但是nuisance提高accuracy和BLEU得分

下表则是展示了不同的模型结构（超参数）的性能差别：

实际上可修改的参数不多，主要就是
层数（$N$）、向量维度（$d_{model}$）、头数（$h$）。

像$d_k,d_v$都是根据$d_{model}$和$h$算出来的。

李沐点评

写作上

这篇文章写的非常简洁，没有太多的介绍和解释，属于大佬的写作风格。不过对于我们大多数研究者来说，还是需要尽可能把背景解释清楚，在正文花足够的篇幅在把故事讲清楚，从而让读者更好理解、认识的更深入。

Transformer

这个模型的最大意义在于给NLP届乃至CV、audio等其他模态的数据提供了统一的模型架构，有点类似于CNN刚提出时对CV领域的巨大变革。有了Transformer，以及现在各种基于Transformer的预训练模型、其他模态的成功运用，Transformer对于多模态学习的进步有着深远的意义。

然后，纵使Transformer已经提出了多年，我们对Transformer的真正原理依然缺乏理解。例如，文章的标题Attention is all you need实际上也是不对的，后续的研究者已经证明Transformer的成功对于MLP、residual connection等其他组件也是缺一不可的，attention的作用就是对序列的信息做了聚合，并不是attention一个人起了全部作用。

另外，self-attention相比如RNN、CNN等的优势，可能在于它所作的归纳偏置（inductive bias）更加一般化，所以经过大规模的训练，可以学习到更丰富、更一般化的知识。但代价就是它对数据的关键信息的抓取能力就下降了，我们需要更多的数据更大的模型才能训练出理想的效果。

但Transformer的出现，给了整个AI届新的活力，让我们发现在CNN、RNN统治的时代，我们依然可以设计出新的网络结构发光发热，因此也带动了一系列新的网络架构设计，比如纯MLP的模型等等。