简介
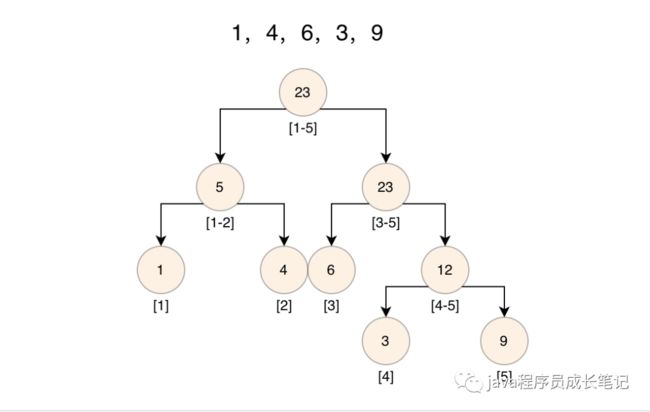
线段树是一种二叉搜索树,是用来维护区间信息的数据结构。可以在O(logN)的时间复杂度内实现单点修改、区间修改、区间查询(区间求和,求区间最大值,求区间最小值)等操作。接下来我以实现区间求和为例子来讲解线段树(最大值和最小值与求和实现方式几乎无异),假设存在一个数组[1,4,6,3,9]。
实现思路
从线段树的定义,我们首先需要定义一个树节点,节点包含区间和(23),区间([1-5]),左节点,右节点等。(如果要实现求区间最大值,最小值,则还需包含这些)。然后需要提供构建线段树,线段树支持修改节点操作方法。
节点定义
@Data
public static class Node {
//区间起始下标
private int start;
//区间结尾下标
private int end;
//当前区间和值
private int value;
private Node left;
private Node right;
Node(int start, int end, int value) {
this.start = start;
this.end = end;
this.value = value;
}
}
构建线段树
因为构建线段树时候需要计算当前区间和,所以我们可以先初始化一个前缀和数组,在构建线段树时候利用下标快速计算出区间和,同时为了保证每个节点有一致的操作,初始化一个头节点,指向root(这是链表树等常用的简化操作的方法)
//head 指向线段树root节点的指针,使得root节点与其余节点操作保持一致 Node head; int size; Listnums; //前缀和数组,便于构建线段树时候计算区间值,用于初次构建辅助 List prefixSum ; public void init(List nums) { //初始化一个头节点,便于操作 this.head = new Node(-1, -1, -1); this.nums = nums; //初始化前缀和数组 prefixSum = new ArrayList<>(nums.size()); prefixSum.add(0); for (int i = 0; i < nums.size() ; i++) { prefixSum.add(prefixSum.get(prefixSum.size() - 1) + nums.get(i)); } //构建线段树 this.build(1, nums.size()); size = nums.size(); } //构建线段树 public void build(int start, int end) { Node root = new Node(start, end, prefixSum.get(end) - prefixSum.get(start - 1)); //将头节点右子树指向root head.right = root; //从root开始构建线段树 this.madeChild(root, start, end); } private void madeChild(Node node, int start, int end) { if (start >= end) { return; } //分个左右子树,左子树取start~mid,右子树取mid+1~end int mid = start + ((end - start) >> 1); if (start <= mid) { Node left = new Node(start, mid, prefixSum.get(mid) - prefixSum.get(start - 1)); node.left = left; madeChild(left, start, mid); } if (mid + 1 <= end) { Node right = new Node(mid + 1, end, prefixSum.get(end) - prefixSum.get(mid)); node.right = right; madeChild(right, mid + 1, end); } }
求解区间和
求解区间和过程就是遍历线段树,将求解区间与当前节点区间进行比较,如果全部存在于左子树或者右子树,则直接深度继续在左子树右子树遍历即可,但是如果求解区间在当前节点的左右子树均有部分,则需要将当前区间分为两个部分,然后分别深度遍历左右子树,最后将结果相加。
//求解区间和
public int findSectionSum(int start, int end) {
//深度遍历线段树,找到对应区间
if (start < 1 || end > size || start > end) {
return -1;
}
return dfsFindSectionSum(head.right, start, end);
}
/**
* 深度遍历线段树结构,分为三种情况
* 1.区间在当前节点的左子树中
* 2.区间在当前节点的右子树中
* 3.左子树中一部分,右子树中一部分
* @param node
* @param start
* @param end
* @return
*/
private int dfsFindSectionSum(Node node, int start, int end) {
if (node.start == start && node.end == end) {
//找到区间
return node.value;
}
if (this.isContain(node.left.start, node.left.end, start, end)) {
//在左子树中
return this.dfsFindSectionSum(node.left, start, end);
}
if (this.isContain(node.right.start, node.right.end, start, end)) {
//包含在右子树中
return this.dfsFindSectionSum(node.right, start, end);
}
//左边一部分,右边一部分
return this.dfsFindSectionSum(node.left, start, node.left.end) + this.dfsFindSectionSum(node.right, node.right.start, end);
}
/**
* 判断区间[start2, end2]是否包含在[start1, end1]中
* @param start1
* @param end1
* @param start2
* @param end2
* @return
*/
private boolean isContain(int start1, int end1, int start2, int end2){
return start2 >= start1 && end2 <= end1;
}
更新线段树
当更新指定位置元素的值的时候,我们需要将线段树中区间包含该节点的区间和进行更新。我们可以从根节点开始深度遍历线段树,如果当前节点包含该位置,我们更新区间和,然后根据当前节点左右子节点的区间,判断走左子树还是右子树,直至更新到叶子节点,则更新完成。
//更新线段树,将index位置的值更新为value,需要更新沿路的值
public void update(int index, int value) {
Node root = head.right;
while (null != root) {
if (index >= root.start && index <= root.end) {
root.value += value - nums.get(index - 1);
}
int mid = root.start + ((root.end - root.start) >> 1);
if (index <= mid) {
root = root.left;
continue;
}
root = root.right;
}
nums.set(index - 1, value);
}
以上就是Java数据结构之线段树的原理与实现的详细内容,更多关于Java 线段树的资料请关注脚本之家其它相关文章!