一文读懂IoU,GIoU, DIoU, CIoU, Alpha-IoU (代码非常优雅)
IoU就是就是我们说的交并比 Intersection over Union ,具体就是两个box的交集除以并集。
当我们计算我们的anchors 或者 proposals 与 ground truth bounding boxes 的损失的时候,就需要用到IoU。不同的IoU有不同的特性。
IoU loss:
IoU计算了最简单的情况:

IoU的损失函数公式:至于求loss为啥用1减去,是因为:iou越大 代表拟合效果越好,我们应让模型的loss越小。iou最大为1,也就是重合的情况。因此用1-IoU来代表loss。
L o s s I o U = 1 − I o U Loss_{IoU}=1- IoU LossIoU=1−IoU
GIoU loss:
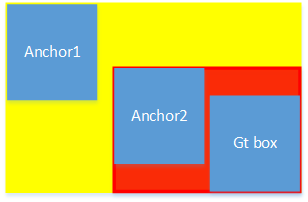
当两个anchor与gt box都不相交的时候,IoU的loss是一样大的,我们理论认为anchor距离gt box越近,loss应该越小,不应该一样大。这样GIoU就提出来了。GIoU通过计算两个box的最小闭包区域ac来计算loss。底色为红色的范围是Anchor2与Gt box的最小闭包区域,底色为黄色的范围是Anchor1与Gt box的最小闭包区域。明显Anchor2的最小闭包区域小,u代表并集,ac代表最小闭包区域,ac越大, L G I o U L_{GIoU} LGIoU 值越大。Anchor1的ac大,所以Anchor1的损失更高
L G I o U = 1 − I o U + a c − u a c L_{GIoU}=1- IoU+\frac{ac-u}{ac} LGIoU=1−IoU+acac−u
DIoU loss:
黄色为proposal,蓝色为gt box。当propsals与gt box重叠时,我们认为下面的两种情况左边的效果好,因为它位于gt box中心。GIoU并不能解决这个问题,所以DIoU loss被提出来了,DIoU loss用,两个box中心点距离平方 除以 最小闭包区域对角线距离平方,来衡量预测的proposal是否位于gt box中心。
L o s s D I o U = 1 − ( I o U + ρ 2 ( b , b g t ) c 2 ) Loss_{DIoU}=1-(IoU+\frac{\rho^2 (b,b^{gt})}{c^2}) LossDIoU=1−(IoU+c2ρ2(b,bgt))
CIoU loss:
当两个proposals都位于gt box中心时,我们还是认为坐标的效果比较好,因为左边的宽高比跟我们的gt box一致,所以CIoU loss在DIoU loss的基础上改进了宽高比。
L o s s C I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 + α v Loss_{CIoU}=1-IoU+\frac{\rho^2 (b,b^{gt})}{c^2}+\alpha v LossCIoU=1−IoU+c2ρ2(b,bgt)+αv
v用来度量长宽比的相似性, 4 π 2 \frac{4}{\pi^2} π24是作者感觉这个值取得的效果不错,就用了这个值。
v = 4 π 2 ( a r c t a n w g t h g t − a r c t a n w h ) 2 v=\frac{4}{\pi^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h}) ^2 v=π24(arctanhgtwgt−arctanhw)2
alpha是权重值,衡量ciou公式中第三项和第四项的权重,当IoU越大,alpha就越大,alpha大就优先考虑v; IoU越小时,alpha越小,alpha小优先考虑第三项,距离比。
α = v ( 1 − I o U ) + v \alpha=\frac{v}{(1-IoU)+v} α=(1−IoU)+vv
Alpha-IoU loss:
Alpha-IoU loss主要是考虑IoU大于0.5的时候的梯度,因为在普通 L I o U = 1 − I o U L_{IoU}=1-IoU LIoU=1−IoU 中,IoU的梯度一直是-1。但是在Alpha-IoU loss中,当iou大于0.5的时候,loss的梯度是大于-1的,收敛的更快,在map0.7/map0.9有提升效果。
L o s s α − I o U = 1 − I o U α Loss_{\alpha-IoU}=1-IoU^{\alpha} Lossα−IoU=1−IoUα
α > 0 \alpha>0 α>0,当 α = 2 , i o u = 0.6 \alpha=2,iou=0.6 α=2,iou=0.6 时, L α − I o U L_{\alpha-IoU} Lα−IoU 的梯度已经是-1.2了。训练时经验所得alpha取3比较好。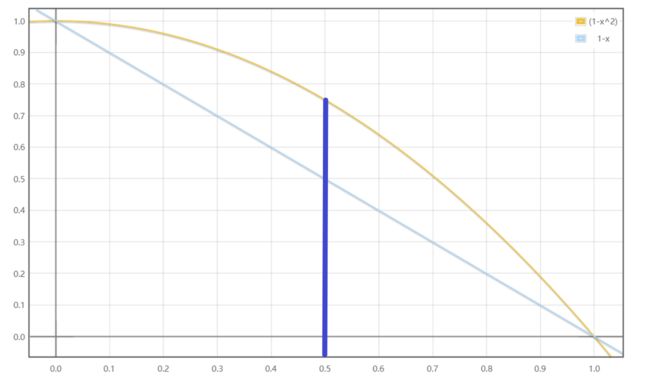
下面是常见的loss function的代码实现。
import torch
import math
import torch.nn.functional as F
# 放到编辑器里收缩每个方法,直接看main函数,然后再对应loss去看。
################################# 分类损失 ########################################
def BCE_loss(proposals, gt_boxes):
# 对所求概率进行 clamp ,不然当某一概率过小时,进行 log ,会让 loss 变为 nan
proposals = proposals.clamp(min=0.0001, max=1.0)
diff = gt_boxes * torch.log(proposals) + (1 - gt_boxes) * (torch.log(1 - proposals))
loss = -torch.mean(diff)
return loss
def CE_loss(proposals, gt_boxes_classid):
loss = 0
# 对所求概率进行 clamp ,不然当某一概率过小时,进行 log ,会让 loss 变为 nan
proposals = proposals.clamp(min=0.0001, max=1.0)
# method1:
for i in range(proposals.shape[0]):
fenzi = torch.exp(proposals[i][gt_boxes_classid[i]]) # proposals中对应真实类别的置信度
fenmu = torch.sum(torch.exp(proposals[i])) # 所有类别的置信度
loss += -torch.log(fenzi / fenmu)
# method2:
# for i in range(proposals.shape[0]):
# first=-proposals[i][gt_boxes_classid[i]]
# second=torch.log(torch.sum(torch.exp(proposals[i])))
# loss+=first+second
return loss / proposals.shape[0]
################################# 位置损失 ########################################
def L1_loss(proposals, gt_boxes):
# 优点:鲁棒性好,因为梯度各个地方都为1,所以对异常值不是那么敏感。
# 缺点:不稳定解,达不到最优解,也就是函数最低点。
# 也叫MAE,平均绝对误差,预测值和真实值之间距离的平均值
diff = torch.abs(gt_boxes - proposals)
loss = torch.mean(diff)
return loss
def L2_loss(proposals, gt_boxes):
# 优点:稳定解,能够达到最优解,也就是函数最低点。
# 缺点:鲁棒性差,对异常值敏感,容易形成梯度爆炸。
# 也叫MSE,均方误差。预测值和真实值之差的平方的平均值。
diff = torch.pow(gt_boxes - proposals, 2)
loss = torch.mean(diff)
return loss
def Smooth_l1_loss(proposals, gt_boxes):
diff = torch.abs(gt_boxes - proposals)
diff = torch.where(diff < 1, 0.5 * diff * diff, diff - 0.5)
loss = torch.mean(diff)
return loss
def IoU_loss(boxa, boxb):
"""
boxa/boxb:Tensor [x1,y1,x2,y2], x2,y2保证大于x1,y1
loss = 1 - iou
"""
inter_x1, inter_y1 = torch.maximum(boxa[:, 0], boxb[:, 0]), torch.maximum(boxa[:, 1], boxb[:, 1])
inter_x2, inter_y2 = torch.minimum(boxa[:, 2], boxb[:, 2]), torch.minimum(boxa[:, 3], boxb[:, 3])
inter_h = torch.maximum(torch.tensor([0]), inter_y2 - inter_y1)
inter_w = torch.maximum(torch.tensor([0]), inter_x2 - inter_x1)
inter_area = inter_w * inter_h
union_area = ((boxa[:, 3] - boxa[:, 1]) * (boxa[:, 2] - boxa[:, 0])) + \
((boxb[:, 3] - boxb[:, 1]) * (boxb[:, 2] - boxb[:, 0])) - inter_area + 1e-8 # + 1e-8 防止除零
iou = inter_area / union_area
iou_loss = 1 - iou
return iou_loss
def GIoU_loss(boxa, boxb):
"""
# 为了解决当两个bbox不相交时,距离远的和距离近的损失值一样大。我们认为距离近的损失应该小一点。
# 注意:划分anchor是否是正样本的时候,anchor与label不一定相交,这样giou能够起到积极的作用
# 当用正样本计算与label的iou损失时,这时候正样本与label都是相交的情况,这时候GIoU不一定起到积极的作用。
giou = iou-(|ac-u|)/|ac| ac最小闭包区域,u并集
loss = 1 - giou
"""
inter_x1, inter_y1 = torch.maximum(boxa[:, 0], boxb[:, 0]), torch.maximum(boxa[:, 1], boxb[:, 1])
inter_x2, inter_y2 = torch.minimum(boxa[:, 2], boxb[:, 2]), torch.minimum(boxa[:, 3], boxb[:, 3])
inter_h = torch.maximum(torch.tensor([0]), inter_y2 - inter_y1)
inter_w = torch.maximum(torch.tensor([0]), inter_x2 - inter_x1)
inter_area = inter_w * inter_h
union_area = ((boxa[:, 3] - boxa[:, 1]) * (boxa[:, 2] - boxa[:, 0])) + \
((boxb[:, 3] - boxb[:, 1]) * (boxb[:, 2] - boxb[:, 0])) - inter_area + 1e-8 # + 1e-8 防止除零
# 求最小闭包区域的x1,y1,x2,y2,h,w,area
ac_x1, ac_y1 = torch.minimum(boxa[:, 0], boxb[:, 0]), torch.minimum(boxa[:, 1], boxb[:, 1])
ac_x2, ac_y2 = torch.maximum(boxa[:, 2], boxb[:, 2]), torch.maximum(boxa[:, 3], boxb[:, 3])
ac_w = ac_x2 - ac_x1
ac_h = ac_y2 - ac_y1
ac_area = ac_w * ac_h
giou = (inter_area / union_area) - (torch.abs(ac_area - union_area) / ac_area)
giou_loss = 1 - giou
return giou_loss
def DIoU_loss(boxa, boxb):
"""
# 当boxes与真实box重合时,一个在中间重合,一个在边缘重合,我们认为在中间重合的是比较好的,
# 所以提出计算两个box中心点的距离,因为预测小目标的中心点box与真实值box本来距离就很小,
# 所以再除以一个最小闭包区域对角线长度,来平衡小目标和大目标的diou。都用平方不开根号减少计算量和精度损失。
diou=iou-两个box中心点距离平方/最小闭包区域对角线距离平方
loss=1-diou
"""
# 求交集
inter_x1, inter_y1 = torch.maximum(boxa[:, 0], boxb[:, 0]), torch.maximum(boxa[:, 1], boxb[:, 1])
inter_x2, inter_y2 = torch.minimum(boxa[:, 2], boxb[:, 2]), torch.minimum(boxa[:, 3], boxb[:, 3])
inter_h = torch.maximum(torch.tensor([0]), inter_y2 - inter_y1)
inter_w = torch.maximum(torch.tensor([0]), inter_x2 - inter_x1)
inter_area = inter_w * inter_h
# 求并集
union_area = ((boxa[:, 3] - boxa[:, 1]) * (boxa[:, 2] - boxa[:, 0])) + \
((boxb[:, 3] - boxb[:, 1]) * (boxb[:, 2] - boxb[:, 0])) - inter_area + 1e-8 # + 1e-8 防止除零
# 求最小闭包区域的x1,y1,x2,y2
ac_x1, ac_y1 = torch.minimum(boxa[:, 0], boxb[:, 0]), torch.minimum(boxa[:, 1], boxb[:, 1])
ac_x2, ac_y2 = torch.maximum(boxa[:, 2], boxb[:, 2]), torch.maximum(boxa[:, 3], boxb[:, 3])
# 把两个bbox的x1,y1,x2,y2转换成ctr_x,ctr_y
boxa_ctrx, boxa_ctry = boxa[:, 0] + (boxa[:, 2] - boxa[:, 0]) / 2, boxa[:, 1] + (boxa[:, 3] - boxa[:, 1]) / 2
boxb_ctrx, boxb_ctry = boxb[:, 0] + (boxb[:, 2] - boxb[:, 0]) / 2, boxb[:, 1] + (boxb[:, 3] - boxb[:, 1]) / 2
# 求两个box中心点距离平方length_box_ctr,最小闭包区域对角线距离平方length_ac,以及diou
length_box_ctr = (boxb_ctrx - boxa_ctrx) * (boxb_ctrx - boxa_ctrx) + \
(boxb_ctry - boxa_ctry) * (boxb_ctry - boxa_ctry)
length_ac = (ac_x2 - ac_x1) * (ac_x2 - ac_x1) + (ac_y2 - ac_y1) * (ac_y2 - ac_y1)
# 求平方,相乘是最快的
iou = inter_area / (union_area + 1e-8)
diou = iou - length_box_ctr / length_ac
diou_loss = 1 - diou
return diou_loss
def CIoU_loss(boxa, boxb):
"""
# 当boxes与真实box重合时,且都在在中心点重合时,一个长宽比接近真实box,一个差异很大
# 我们认为长宽比接近的是比较好的,损失应该是比较小的。所以ciou增加了对box长宽比的考虑
ciou=iou+两个box中心点距离平方/最小闭包区域对角线距离平方+alpha*v
loss=1-iou+两个box中心点距离平方/最小闭包区域对角线距离平方+alpha*v
注意loss跟上边不一样,这里不是1-ciou
v用来度量长宽比的相似性,4/(pi *pi)*(arctan(boxa_w/boxa_h)-arctan(boxb_w/boxb_h))^2
alpha是权重值,衡量ciou公式中第二项和第三项的权重,
alpha大优先考虑v,alpha小优先考虑第二项距离比,alpha = v / ((1 - iou) + v)。
"""
# 求交集
inter_x1, inter_y1 = torch.maximum(boxa[:, 0], boxb[:, 0]), torch.maximum(boxa[:, 1], boxb[:, 1])
inter_x2, inter_y2 = torch.minimum(boxa[:, 2], boxb[:, 2]), torch.minimum(boxa[:, 3], boxb[:, 3])
inter_h = torch.maximum(torch.tensor([0]), inter_y2 - inter_y1)
inter_w = torch.maximum(torch.tensor([0]), inter_x2 - inter_x1)
inter_area = inter_w * inter_h
# 求并集
union_area = ((boxa[:, 3] - boxa[:, 1]) * (boxa[:, 2] - boxa[:, 0])) + \
((boxb[:, 3] - boxb[:, 1]) * (boxb[:, 2] - boxb[:, 0])) - inter_area + 1e-8 # + 1e-8 防止除零
# 求最小闭包区域的x1,y1,x2,y2
ac_x1, ac_y1 = torch.minimum(boxa[:, 0], boxb[:, 0]), torch.minimum(boxa[:, 1], boxb[:, 1])
ac_x2, ac_y2 = torch.maximum(boxa[:, 2], boxb[:, 2]), torch.maximum(boxa[:, 3], boxb[:, 3])
# 把两个bbox的x1,y1,x2,y2转换成ctr_x,ctr_y
boxa_ctrx, boxa_ctry = boxa[:, 0] + (boxa[:, 2] - boxa[:, 0]) / 2, boxa[:, 1] + (boxa[:, 3] - boxa[:, 1]) / 2
boxb_ctrx, boxb_ctry = boxb[:, 0] + (boxb[:, 2] - boxb[:, 0]) / 2, boxb[:, 1] + (boxb[:, 3] - boxb[:, 1]) / 2
boxa_w, boxa_h = boxa[:, 2] - boxa[:, 0], boxa[:, 3] - boxa[:, 1]
boxb_w, boxb_h = boxb[:, 2] - boxb[:, 0], boxb[:, 3] - boxb[:, 1]
# 求两个box中心点距离平方length_box_ctr,最小闭包区域对角线距离平方length_ac
length_box_ctr = (boxb_ctrx - boxa_ctrx) * (boxb_ctrx - boxa_ctrx) + \
(boxb_ctry - boxa_ctry) * (boxb_ctry - boxa_ctry)
length_ac = (ac_x2 - ac_x1) * (ac_x2 - ac_x1) + (ac_y2 - ac_y1) * (ac_y2 - ac_y1)
v = (4 / (math.pi * math.pi)) * (torch.atan(boxa_w / boxa_h) - torch.atan(boxb_w / boxb_h)) \
* (torch.atan(boxa_w / boxa_h) - torch.atan(boxb_w / boxb_h))
iou = inter_area / (union_area + 1e-8)
alpha = v / ((1 - iou) + v)
# ciou = iou - length_box_ctr / length_ac - alpha * v
ciou_loss = 1 - iou + length_box_ctr / length_ac + alpha * v
return ciou_loss
def AlphaIoU_loss(boxa, boxb, alpha):
"""
# 除了alpha-iou,还有alpha-giou, alpha-diou, alpha-ciou,这里就不写了。
# alpha-iou的优点是,例如alpha取2,当iou大于0.5的时候,loss的梯度是大于1的,
# 相比iou的loss一直等于-1,收敛的更快,map0.7/map0.9有提升效果。
loss = 1 - iou^alpha alpha>0,取3效果比较好
"""
inter_x1, inter_y1 = torch.maximum(boxa[:, 0], boxb[:, 0]), torch.maximum(boxa[:, 1], boxb[:, 1])
inter_x2, inter_y2 = torch.minimum(boxa[:, 2], boxb[:, 2]), torch.minimum(boxa[:, 3], boxb[:, 3])
inter_h = torch.maximum(torch.tensor([0]), inter_y2 - inter_y1)
inter_w = torch.maximum(torch.tensor([0]), inter_x2 - inter_x1)
inter_area = inter_w * inter_h
union_area = ((boxa[:, 3] - boxa[:, 1]) * (boxa[:, 2] - boxa[:, 0])) + \
((boxb[:, 3] - boxb[:, 1]) * (boxb[:, 2] - boxb[:, 0])) - inter_area + 1e-8 # + 1e-8 防止除零
iou = inter_area / union_area
alpha_iou = torch.pow(iou, alpha)
alpha_iou_loss = 1 - alpha_iou
return alpha_iou_loss
if __name__ == '__main__':
# 定义一些输入的tensor
proposals = torch.tensor([0., 0., 2., 2.], dtype=torch.float32)
gt_boxes = torch.tensor([1., 1., 5., 5.], dtype=torch.float32)
# 专门用于bce loss的输入
bce_prop = torch.tensor([0.2, 0.7, 0.99, 0.5], dtype=torch.float32)
bce_gt = torch.tensor([0, 1, 0, 1], dtype=torch.float32)
# 专门用于ce loss的输入,4个边界框,每个边界框对应2个类别的置信度
ce_prop = torch.randn([4, 2], dtype=torch.float32)
ce_prop = F.softmax(ce_prop, dim=1) # 对每个bbox的置信度进行softmax
# 4个边界框的真实类别id
ce_gt_boxes_classid = torch.randint(0, 2, [4], dtype=torch.int64)
# 专门用于iou loss的输入
iou_proposals = torch.tensor([[0, 0, 2, 2], [0, 0, 2, 2]])
iou_gt_boxes = torch.tensor([[1, 1, 3, 3], [1, 1, 2, 4]])
########################################### our methods #############################################
# 分类损失:
bce_loss = BCE_loss(bce_prop, bce_gt)
ce_loss = CE_loss(ce_prop, ce_gt_boxes_classid)
# 位置损失:
l1_loss = L1_loss(proposals, gt_boxes) # 也叫MAE
l2_loss = L2_loss(proposals, gt_boxes) # 也叫MSE
smooth_l1_loss = Smooth_l1_loss(proposals, gt_boxes)
iou_loss = IoU_loss(iou_proposals, iou_gt_boxes)
giou_loss = GIoU_loss(iou_proposals, iou_gt_boxes)
diou_loss = DIoU_loss(iou_proposals, iou_gt_boxes)
ciou_loss = CIoU_loss(iou_proposals, iou_gt_boxes) # proposals和gt_boxes宽高比一样,所以ciou等于diou
alphaiou1_loss = AlphaIoU_loss(iou_proposals, iou_gt_boxes, alpha=1)
alphaiou3_loss = AlphaIoU_loss(iou_proposals, iou_gt_boxes, alpha=3)
########################################### official methods #############################################
# 分类损失:
bce_loss_ = F.binary_cross_entropy(bce_prop, bce_gt)
ce_loss_ = F.cross_entropy(ce_prop, ce_gt_boxes_classid)
# 位置损失:
l1_loss_ = F.l1_loss(proposals, gt_boxes) # 也叫MAE
l2_loss_ = F.mse_loss(proposals, gt_boxes) # 也叫MSE
smooth_l1_loss_ = F.smooth_l1_loss(proposals, gt_boxes)
# 输出结果对比一下:
print("bce:",bce_loss)
print("bce_:",bce_loss_)
print("ce:",ce_loss)
print("ce_:",ce_loss_)
print("l1_loss:",l1_loss)
print("l1_loss_:",l1_loss_)
print("l2_loss:",l2_loss)
print("l2_loss_:",l2_loss_)
print("smooth_l1_loss:",smooth_l1_loss)
print("smooth_l1_loss_:",smooth_l1_loss_)
# 自己计算一下,看写的iou loss函数对不对,下面是手动计算的结果:
# 下面我把并集中1e-8省略了,所以会有略微差距。下面手动计算的是[0, 0, 2, 2]与[1, 1, 3, 3]的各种iou loss
# box1 area=4, box2 area=4,inter area=1, union area=7, ac area=9, iou=1/7
print("iou loss:",iou_loss)
print("iou loss:", 1 - 1 / 7)
print("giou loss:",giou_loss)
print("giou loss:", 1 - (1 / 7 - (9 - 7) / 9))
print("diou loss:",diou_loss)
print("diou loss:", 1 - (1 / 7 - (1 * 1) / (3 * 3)))
print("ciou loss:",ciou_loss)
v = 4 / (math.pi * math.pi) * ((math.atan(2 / 2) - math.atan(2 / 2)) * (math.atan(2 / 2) - math.atan(2 / 2)))
print("ciou loss:", 1 - 1 / 7 + (1 * 1) / (3 * 3) + v / ((1 - 1 / 7) + v) * v)
print("alpha1 iou loss:",alphaiou1_loss)
print("alpha1 iou loss:", 1 - 1 / 7)
print("alpha3 iou loss:",alphaiou3_loss)
print("alpha3 iou loss:1", 1 - math.pow((1 / 7), 3))
输出结果:
bce: tensor(1.4695)
bce_: tensor(1.4695)
ce: tensor(0.9038)
ce_: tensor(0.9038)
l1_loss: tensor(2.)
l1_loss_: tensor(2.)
l2_loss: tensor(5.)
l2_loss_: tensor(5.)
smooth_l1_loss: tensor(1.5000)
smooth_l1_loss_: tensor(1.5000)
iou loss: tensor([0.8571, 0.8333])
iou loss: 0.8571428571428572
giou loss: tensor([1.0794, 1.0833])
giou loss: 1.0793650793650793
diou loss: tensor([0.9683, 0.9583])
diou loss: 0.9682539682539683
ciou loss: tensor([0.9683, 0.9666])
ciou loss: 0.9682539682539684
alpha1 iou loss: tensor([0.8571, 0.8333])
alpha1 iou loss: 0.8571428571428572
alpha3 iou loss: tensor([0.9971, 0.9954])
alpha3 iou loss:1 0.9970845481049563

