图神经网络（GNN）的基本原理

前言

本文结合一个具体的无向图来对最简单的一种GNN进行推导。本文第一部分是数据介绍，第二部分为推导过程中需要用的变量的定义，第三部分是GNN的具体推导过程，最后一部分为自己对GNN的一些看法与总结。

1. 数据

利用networkx简单生成一个无向图：

# -*- coding: utf-8 -*-
"""
@Time ： 2021/12/21 11:23
@Author ：KI 
@File ：gnn_basic.py
@Motto：Hungry And Humble

"""
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

G = nx.Graph()
node_features = [[2, 3], [4, 7], [3, 7], [4, 5], [5, 5]]
edges = [(1, 2), (1, 3), (2, 4), (2, 5), (1, 3), (3, 5), (3, 4)]
edge_features = [[1, 3], [4, 1], [1, 5], [5, 3], [5, 6], [5, 4], [4, 3]]
colors = []
edge_colors = []

# add nodes
for i in range(1, len(node_features) + 1):
    G.add_node(i, feature=str(i) + ':(' + str(node_features[i-1][0]) + ',' + str(node_features[i-1][1]) + ')')
    colors.append('#DCBB8A')

# add edges
for i in range(1, len(edge_features) + 1):
    G.add_edge(edges[i-1][0], edges[i-1][1], feature='(' + str(edge_features[i-1][0]) + ',' + str(edge_features[i-1][1]) + ')')
    edge_colors.append('#3CA9C4')

# draw
fig, ax = plt.subplots()

pos = nx.spring_layout(G)
nx.draw(G, pos=pos, node_size=2000, node_color=colors, edge_color='black')
node_labels = nx.get_node_attributes(G, 'feature')
nx.draw_networkx_labels(G, pos=pos, labels=node_labels, node_size=2000, node_color=colors, font_color='r', font_size=14)
edge_labels = nx.get_edge_attributes(G, 'feature')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=14, font_color='#7E8877')

ax.set_facecolor('deepskyblue')
ax.axis('off')
fig.set_facecolor('deepskyblue')
plt.show()

如下所示：

其中，每一个节点都有自己的一些特征，比如在社交网络中，每个节点（用户）有性别以及年龄等特征。

5个节点的特征向量依次为：

[[2, 3], [4, 7], [3, 7], [4, 5], [5, 5]]

同样，6条边的特征向量为：

[[1, 3], [4, 1], [1, 5], [5, 3], [5, 6], [5, 4], [4, 3]]

2. 变量定义

1. 节点特征向量$l_v$：节点$v$的特征向量，如$l_1=(2,3)$。
2. 节点状态向量$x_v$：节点$v$的状态向量。关于节点初始的状态向量，不同的GNN有不同的定义：循环GNN中随机初始化，NN4N中初始时为零向量，而在Gated GNN也就是门控GNN中，初始时的状态向量就为特征向量。最终的状态向量也就是我们学到的节点的高级表示。
3. 边特征向量$l_{(v,u)}$，边$(v,u)$的特征向量，如$l_{(1,2)}=(1,3)$。

特征向量实际上也就是节点或者边的标签，这个是图本身的属性，一直保持不变。

3. GNN算法

GNN算法的完整描述如下：Forward向前计算状态，Backward向后计算梯度，主函数通过向前和向后迭代调用来最小化损失。

主函数中：

1. 首先初始化参数$w$
2. 通过Forward计算出所有节点的收敛的状态向量：$x=Forward(w)$
3. 通过Backward计算：$\frac{\partial e_w}{\partial w}=Backward(x,w)$，利用梯度下降法更新参数$w$：$w=w-\lambda \cdot \frac{\partial e_w}{\partial w}$，最后利用更新后的参数$w$重新对所有节点的状态进行更新：$x=Forward(w)$。重复以上过程。
4. 最后得到的$w$就是我们的GNN了。

上述描述只是一个总体的概述，可以略过先不看。

3.1 Forward

早期的GNN都是RecGNN，即循环GNN。这种类型的GNN基于信息传播机制： GNN通过不断交换邻域信息来更新节点状态，直到达到稳定均衡。节点的状态向量$x$由以下$f_w$函数来进行周期性更新：


解析上述公式：对于节点$n$，假设为节点1，更新其状态需要以下数据参与：

1. $l_n$，节点$n$的特征向量，即：$l_1=(2,3)$。
2. $l_{co[n]}$，与$n$相连的边的特征向量，即[(1, 3), (5, 6)]
3. $x_{ne[n]}(t)$，节点$n$相邻节点（这里为2和3）$t$时刻的状态向量。
4. $l_{ne[n]}$：节点$n$相邻节点的特征向量，这里为节点2和3的特征向量。

这里的$f_w$只是形式化的定义，不同的GNN有不同的定义，如随机稳态嵌入(SSE)中定义如下：

由更新公式可知，当所有节点的状态都趋于稳定状态时，此时所有节点的状态向量都包含了其邻居节点和相连边的信息。

这与图嵌入有些类似：如果是节点嵌入，我们最终得到的是一个节点的向量表示，而这些向量是根据随机游走序列得到的，随机游走序列中又包括了节点的邻居信息， 因此节点的向量表示中包含了连接信息。

证明上述更新过程能够收敛需要用到不动点理论，这里简单描述下：

如果我们有以下更新公式：
$$x(t+1)=F_w(x(t),l)$$
只要$F_w$是压缩映射，那么最终$x$必会收敛到一个固定的点，这个点称为不动点。是否收敛可用以下公式判断：
$$||x(t)-x(t-1)||<{\epsilon }_f$$

GNN的Foward描述如下：

解释：

1. 初始化所有节点的状态向量，此时$t=0$。
2. 然后利用压缩映射$F_w$对节点状态向量进行更新：$x(t+1)=F_w(x(t),l)$，这里的$l$包含三种类型信息：节点的特征向量$l_n$，与节点相连边的特征向量 $l_{co[n]}$以及与节点相连节点的特征向量$l_{ne[n]}$。
3. 如果更新后达到了收敛条件，则停止更新，返回最终时刻所有节点的状态向量。

3.2 Backward

在节点嵌入中，我们最终得到了每个节点的表征向量，此时我们就能利用这些向量来进行聚类、节点分类、链接预测等等。

GNN中类似，得到这些节点状态向量的最终形式不是我们的目的，我们的目的是利用这些节点状态向量来做一些实际的应用，比如节点标签预测。

因此，如果想要预测的话，我们就需要一个输出函数来对节点状态进行变换，得到我们要想要的东西：

最容易想到的就是将节点状态向量经过一个前馈神经网络得到输出，也就是说$g_w$可以是一个FNN，同样的，$f_w$也可以是一个FNN：

我们利用$g_w$函数对节点$n$收敛后的状态向量$x_n$以及其特征向量$l_n$进行变换，就能得到我们想要的输出，比如某一类别，某一具体的数值等等。

在BP算法中，我们有了输出后，就能算出损失，然后利用损失反向传播算出梯度，最后再利用梯度下降法对神经网络的参数进行更新。

对于某一节点的损失（比如回归）我们可以简单定义如下：
$$los{s}_n=(o_n-t_n{)}^2$$
这里的$t_n$是节点的某一标签（比如年龄）。

因此所有节点的损失可以定义为：
$$e_w=\sum _{n\in V}(o_n-t_n{)}^2$$

因为我们要更新$w$，所以我们需要得到损失$e_w$对参数$w$的导数，即算出：
$$\frac{\partial e_w}{\partial w}$$

在GNN中，我们定义$z(t)$如下：

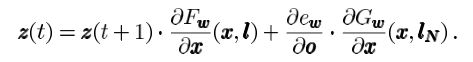
有了$z(t)$后，我们就能求导了：

$e_w={\sum }_{n\in V}(o_n-t_n{)}^2$，所以我们可以直接求$\frac{\partial e_w}{\partial o}$。$\frac{\partial G_w}{\partial w}(x,l_N)$是输出对$w$的导数，$\frac{\partial F_w}{\partial w}(x,l_N)$是状态转换函数对$w$的导数，这两个也能直接算出。

$z(t)$的求解方法在Backward中有描述：

1. 先对Forward后得到的最终节点状态向量进行转换，得到输出$o$
2. 计算状态转换函数对节点状态向量$x$的导数$A=\frac{\partial F_w}{\partial x}(x,l)$
3. 计算$b=\frac{\partial e_w}{\partial o}\cdot \frac{\partial G_w}{\partial x}(x,l_N)$
4. 初始化$z(0)$，此时为0时刻
5. 重复计算：$z(t)=z(t+1)\cdot A+b$，直至$z(t)$收敛
6. 计算$c=\frac{\partial e_w}{\partial o}\cdot \frac{\partial G_w}{\partial w}(x,l_N)$
7. 计算$d=z(t)\cdot \frac{\partial F_w}{\partial w}(x,l)$
8. 最后算出误差对要更新的$w$的导数$\frac{\partial e_w}{\partial w}=c+d$

因此，在Backward中需要计算以下导数：

1. 状态转换函数$F_w$对节点状态$x$的导数$\frac{\partial F_w}{\partial x}$
2. 输出函数$G_w$对节点状态的导数$\frac{\partial G_w}{\partial x}$
3. $G_w$和$F_w$对$w$的导数

4.总结与展望

本文所讲的GNN是最原始的GNN，此时的GNN存在着不少的问题，比如对不动点隐藏状态的更新比较低效。

由于CNN在CV领域的成功，许多重新定义图形数据卷积概念的方法被提了出来，图卷积神经网络ConvGNN也被提了出来，ConvGNN被分为两大类：频域方法（spectral-based method ）和空间域方法（spatial-based method）。2009年，Micheli在继承了来自RecGNN的消息传递思想的同时，在架构上复合非递归层，首次解决了图的相互依赖问题。在过去的几年里还开发了许多替代GNN，包括GAE和STGNN。这些学习框架可以建立在RecGNN、ConvGNN或其他用于图形建模的神经架构上。

GNN是用于图数据的深度学习架构，它将端到端学习与归纳推理相结合，业界普遍认为其有望解决深度学习无法处理的因果推理、可解释性等一系列瓶颈问题，是未来3到5年的重点方向。

因此，不仅仅是GNN，图领域的相关研究都是比较有前景的，这方面的应用也十分广泛，比如推荐系统、计算机视觉、物理/化学（生命科学）、药物发现等等。