顺序表的实现
1.概念及结构
顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存
储。在数组上完成数据的增删查改。
顺序表一般可以分为静态顺序表和动态顺序表
注:顺序表的英文是sequence list,以下简写为SL
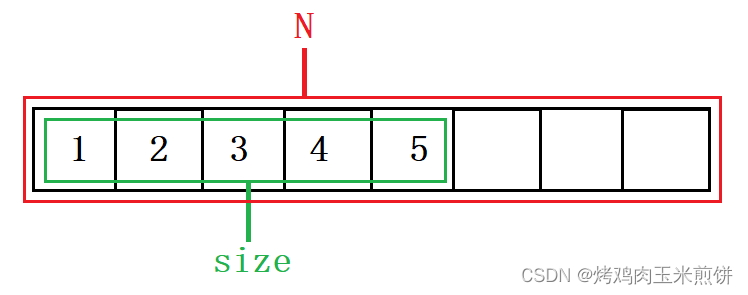
静态顺序表:使用定长数组存储元素。
#define N 8
typedef int SLDateType;
typedef struct SL
{
SLDateType a[N]; //定长数组
int size; //有效数据的个数
}SL;
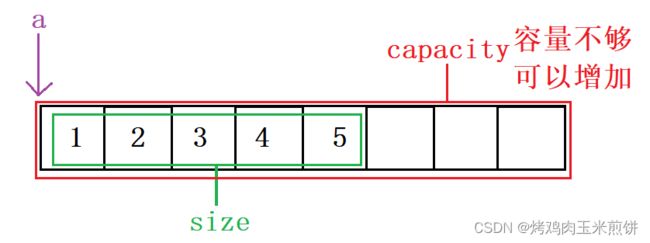
动态数据表:使用动态开辟的数组存储
#define N 8
typedef int SLDateType;
typedef struct SL
{
SLDateType* a; //指向动态开辟的数组
int size; //有效数据的个数
int capacity; //数组的容量大小
}SL;
2 接口实现
静态顺序表只适用于确定知道需要存多少数据的场景。静态顺序表的定长数组导致N定大了,空
间开多了浪费,开少了不够用。所以现实中基本都是使用动态顺序表,根据需要,动态的分配空间
大小,所以下面我们来实现动态顺序表。
分三个模块来写 (完整代码在结尾处)
SL.h用来来声明类型和声明函数,引用库文件
SL.c用来写函数的实现
test.c用来测试
这个顺序表主要实现增删查改的功能
首先在SL.h中引用头文件和完成结构类型的声明
#include
#include
#include
#define N 8
typedef int SLDateType;
typedef struct SL
{
SLDateType* a; //指向动态开辟的数组
int size; //有效数据的个数
int capacity; //数组的容量大小
}SL;
之后可以尝试往顺序表中添加数据,而在添加数据之前,需要先对其进行初始化
SL.h
//初始化
void SLInit(SL* ps);
SL.c
void SLInit(SL* ps)
{
assert(ps);
ps->a = NULL;
ps->size = 0;
ps->capacity = 0;
}
在完成初始化之后,开始往顺序表中添加数据,要检查容量是否足够,如果不够,就要对其进行扩容,首先实现在顺序表的尾部增加数据
SL.h
//尾增
void SLPushBack(SL* ps, SLDateType x);
SL.c
void SLPushBack(SL* ps, SLDateType x)
{
assert(ps);
//检查容量
if (ps->size == ps->capacity)
{
int NewCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
SLDateType* tmp = (SLDateType*)realloc(ps->a, NewCapacity * sizeof(SLDateType));
if (tmp == NULL)
{
printf("realloc fail\n");
return;
}
ps->a = tmp;
ps->capacity = NewCapacity;
}
ps->a[ps->size] = x;
ps->size++;
}
在实现了数据的增加之后,应该需要写一个函数来打印数据
SL.h
//打印
void SLPrint(SL* ps);
SL.c
void SLPrint(SL* ps)
{
assert(ps);
int i = 0;
for (i = 0; i < ps->size; i++)
{
printf("%d ", ps->a[i]);
}
printf("\n");
}
由于顺序表的数据时动态内存中存储的,所以需要释放内存,也就是销毁顺序表的数据
SL.h
//销毁
void SLDestroy(SL* ps);
SL.c
void SLDestroy(SL* ps)
{
assert(ps);
if (ps->a)
{
free(ps->a);
ps->a = NULL;
ps->size = 0;
ps->capacity = 0;
}
}
然后可以实现在数据表的尾部删除数据
SL.h
//尾删
void SLPopBack(SL* ps);
SL.c
void SLPopBack(SL* ps)
{
assert(ps);
assert(ps->size > 0);
ps->size--;
}
接着可以在头部增加数据和删除数据,由于在头部和在尾部增加数据都需要涉及到数据容量的检查,所以可以把容量检查部分的代码单独写一个函数
SL.c
void SLCapacityCheck(SL* ps)
{
if (ps->size == ps->capacity)
{
int NewCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
SLDateType* tmp = (SLDateType*)realloc(ps->a, NewCapacity * sizeof(SLDateType));
if (tmp == NULL)
{
printf("realloc fail\n");
return;
}
ps->a = tmp;
ps->capacity = NewCapacity;
}
}
SL.h
//头增
void SLPushFront(SL* ps, SLDateType x);
//头删
void SLPopFront(SL* ps);
SL.c
void SLPushFront(SL* ps, SLDateType x)
{
assert(ps);
SLCapacityCheck(ps);
int end = ps->size;
while (end > 0)
{
ps->a[end] = ps->a[end - 1];
end--;
}
ps->size++;
ps->a[0] = x;
}
void SLPopFront(SL* ps)
{
assert(ps);
assert(ps->size > 0);
int begin = 1;
while (begin < ps->size)
{
ps->a[begin - 1] = ps->a[begin];
begin++;
}
ps->size--;
}
如果要实现在任意位置增加和删除的数据,就需要在上面函数的基础上做一点改进,比如参数部分增加一个下标来定位
SL.h
//指定位置增加
void SLInsert(SL* ps, int pos, SLDateType x);
//指定位置删除
void SLErase(SL* ps, int pos);
SL.c
void SLInsert(SL* ps, int pos, SLDateType x)
{
assert(ps);
assert(pos >= 0);
SLCapacityCheck(ps);
int end = ps->size - 1;
while (end >= pos)
{
ps->a[end + 1] = ps->a[end];
end--;
}
ps->a[pos] = x;
ps->size++;
}
void SLErase(SL* ps, int pos)
{
assert(ps);
assert(pos >= 0);
assert(ps->size > 0);
int begin = pos + 1;
while (begin < ps->size)
{
ps->a[begin - 1] = ps->a[begin];
begin++;
}
ps->size--;
}
而头增和头删,尾增和尾删,都可以归类到任意位置增加和任意位置删除里面来,所以可以对头增和头删,尾增和尾删函数进行一些修改
SL.c
void SLPushBack(SL* ps, SLDateType x)
{
assert(ps);
SLInsert(ps, ps->size, x);
}
void SLPopBack(SL* ps)
{
assert(ps);
SLErase(ps, ps->size);
}
void SLPushFront(SL* ps, SLDateType x)
{
assert(ps);
SLInsert(ps, 0, x);
}
void SLPopFront(SL* ps)
{
assert(ps);
assert(ps->size > 0);
SLErase(ps, 0);
}
而顺序表的查找和修改功能的实现就比较简单了
SL.h
//查找
int SLFind(SL* ps, SLDateType x);
//修改
void SLModify(SL* ps, int pos, SLDateType x);SL.c
int SLFind(SL* ps, SLDateType x)
{
assert(ps);
int i = 0;
for (i = 0; i < ps->size; i++)
{
if (ps->a[i] == x)
{
return i;
}
}
return -1;
}
void SLModify(SL* ps, int pos, SLDateType x)
{
assert(ps);
assert(pos >= 0 && ps->size > 0);
ps->a[pos] = x;
}3.练习
1.https://leetcode.cn/problems/remove-element/
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
2.https://leetcode.cn/problems/remove-duplicates-from-sorted-array/
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。
由于在某些语言中不能改变数组的长度,所以必须将结果放在数组nums的第一部分。更规范地说,如果在删除重复项之后有 k 个元素,那么 nums 的前 k 个元素应该保存最终结果。
将最终结果插入 nums 的前 k 个位置后返回 k 。
不要使用额外的空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
3.https://leetcode.cn/problems/merge-sorted-array/
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
4.顺序表的问题
1. 中间/头部的插入删除,时间复杂度为O(N)。
2. 增容需要申请新空间,拷贝数据,释放旧空间。会有不小的消耗。
3. 增容一般是呈2倍的增长,势必会有一定的空间浪费。例如当前容量为100,满了以后增容到200,我们再继续插入了5个数据,后面没有数据插入了,那么就浪费了95个数据空间。