机器学习笔记5-0：卷积神经网络

*注:本博客参考李宏毅老师2020年机器学习课程. 视频链接

---

0 引言

CNN时卷积神经网络的简称，它被广泛用于图像和语音领域，CNN的提出大幅减少了全连接神经网络的参数量，并且性能也比全连接神经网络更高。

1 图像识别的特点

1.1 全连接神经网络的缺点

假设有一张512*512像素的图片需要被全连接神经网络处理，若网络的第一个隐藏层包含1000个神经元，那么仅仅时第一层，就需要512*512*1000=262144000个参数！

(图1)

如此庞大的参数量必然导致两种结果：模型体积巨大，计算速度极慢。然而这样庞大的参数量是必须的吗？我们知道，对于一个深层的神经网络，较浅层的神经元往往学习到图像最基本的特征，较深层的神经元又对浅层特征进行抽象，得到高维的特征。对于特征的检测，我们知道有以下三个特点：

1.2 特征的局部性

对于一张图片而言，例如图一中的猫，如果网络需要检测图片中是否是一只猫，浅层神经元可能需要检测图片中是否有眼睛、鼻子、耳朵等。在全连接神经网络中，一个神经元将连接图片的每一个像素点，然而对于这个神经元来说，即使仅仅输入了图片的一小部分，只要这一部分图像中包含着它所要检测的特征，该神经元依然可以检测出特征，因此不需要将整个图像输入给该神经元。

1.3 检测器权值共享

对于同一个特征，在不同的图像中，它可能存在于不同的位置，而不管该特征存在于哪个位置，用于检测该特征的神经元所要做的工作都是一样的，所以其参数也应该一样，这称为权值共享。

1.4 下采样

所谓的下采样，是在一张图像中，每隔一定数量的像素点，采样一次，将所有被采样的像素构成一张新的图像。这样做能够减小图像的尺寸，并且不会影响特征的检测。

2 CNN

2.1 CNN基本结构

结合上述三个特点，CNN的思想就呼之欲出了：为了共享权值，我们使用一个神经元来检测所有相同的特征；为了利用特征的局部性，我们利用一个“窗口”，每次只将图像被窗口围住的一部分传递给该神经元。同时，由于我们事前不知道特征位于图像的哪个位置，因此这个窗口必须滑过整个图像，称为“滑动窗口”，滑动窗口与神经元的运算被称为卷积。在完成一次卷积之后，由于图像与特征下采样一般都不会影响后续特征的识别，因此可以对其进行下采样。

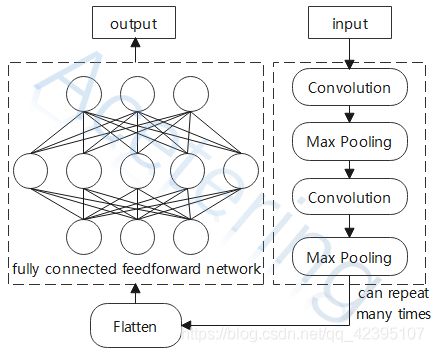
在前述过程中，图像一直是以2维的形式参与运算，运算结束后将得到一个包含高维特征的矩阵，我们先将该矩阵拉长成一个向量，最后送入全连接神经网络，由全连接神经网络结合所有的特征，决定该图像的类别。整个CNN的基本结构如图2所示：

(图2)

2.2 卷积运算

卷积运算的过程如下图：

(图3)
在卷积运算中，涉及到如下几个概念：

• 卷积核：参与卷积运算的矩阵，一般行列相等；
• 步长：每次卷积核移动的距离。

在图3中，我们使用了一个2*2的卷积核，对一个4*4的矩阵进行卷积运算，步长设置为1，计算时首先将卷积核置于被积矩阵的左上角，然后将卷积核与被积矩阵做内积（即对应位置相乘再求和），得到结果矩阵左上角的值，然后将卷积核向右移动步长所指定的距离，重复上述操作，指导卷积核掠过被积矩阵所有的位置。

一般地，假设被积矩阵为$M$阶矩阵，卷积核为$N$阶矩阵，步长为$S$，那么得到的结果矩阵的阶数为：
$$out\_size=\frac{M-N}{S}+1$$

如果我们的输入不是一个二维的矩阵，而是更高维的情况，例如一张彩色的图片，包含三个颜色通道RGB。此时我们进行卷积运算的卷积核也应该对每一个通道单独设置一个矩阵，称为filter，进行卷积运算时，不同通道的被积矩阵和filter互不影响，每个filter只对其对应的通道进行卷积运算。运算结束之后，得到的结果也应该包含3个通道，我们称该结果为Feature Map。

2.3 卷积与全连接的关系

事实上，卷积运算并不是与全连接网络的计算完全不同，卷积运算是全连接网络的一种特殊情况。我们可以将图3中的卷积运算展开，变成图4的形式：

(图4)

从图4中可以看出，所谓的卷积核，其实是神经元的一种表现形式：在图4中，我们将位于被积矩阵左上角的卷积核当作第一个神经元的参数，将向右移动一格之后的卷积核当作第二个神经元的参数……，以此类推，我们可以完整的画出一个具有9个神经元的神经网络，但是，这里的每个神经元并不与每一个输入连接，而是仅仅连接了4个输入，除此之外，所有神经元的参数其实是一样的——均等于卷积核中的值。

于是，通过使用卷积，我们共享了不同神经元之间的参数，将原本需要$9\ast 16$个参数的神经网络，参数量减小到了4个，大大缩减了网络的体积和运算量。

2.4 Max Pooling

Max Pooling（最大池化）所要做的事情是，将Feature Map中的值按k*k分组，然后取每一个组中最大的那一个值，构成一个新的矩阵，例如：

(图5)

容易发现，经过Max Pooling之后，原本较大的矩阵将会变小，这使得后续运算的输入规模变小，从而减小计算量。

2.5 Flatten

Flatten也就是将矩阵拉直成为一个向量，因为神将网络的输入是一个向量，所以在送入全连接神将网络之前，我们首先需要把原本是矩阵形式的中间输出变成向量。这一步操作在图4的第一个变形中也有体现。

3 PyTorch实现：CNN分类MNIST

在前面的章节中，我们仅仅使用了全连接神将网络来对MNIST数据集进行分类。在这一节中，我们使用CNN进一步改进这个模型。

3.1 网络结构定义

首先定义网络结构，这里使用到了两个新方法：

• nn.Conv2d方法，该方法的前两个参数分别传递卷积层的输入和输出的size，kernel_size指定卷积核的size，stride指定步长；
• nn.MaxPool2d方法，表示最大池化操作，通过参数kernel_size指定分组大小。

在本文的示例中，输入数据经过两个卷积核大小为3，步长为1的卷积层，每个卷积层之后都经过ReLU激活，并通过size为2的最大池化逐步减小尺寸。完成上述操作之后，送入一个简单的全连接神将网络，该网络包含一个隐藏层，10个神经元，输入前先进行Flatten拉伸为向量，最后经过ReLU激活，得到输出。注：在下述实现过程中，网络初始化传入一个参数x，用于自适应地调整全连接层的输入尺寸。下面给出了网络结构的定义：

import torch.nn as nn
class Model(nn.Module):
    def __init__(self, x):
        super(Model, self).__init__()
        self.layer1 = nn.Sequential(
            nn.Conv2d(1, 16, kernel_size=3, stride=1),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2)
        )
        self.layer2 = nn.Sequential(
            nn.Conv2d(16, 8, kernel_size=3),
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2)
        )
        x = self.layer1(x)
        x = self.layer2(x)
        input_size = nn.Flatten()(x).shape[1]
        self.layer_fc = nn.Sequential(
            nn.Flatten(),
            nn.Linear(input_size, 10),
            nn.ReLU()
        )

    def forward(self, x):
        x = self.layer1(x)
        x = self.layer2(x)
        y = self.layer_fc(x)
        return y

关于数据组织和训练过程的定义，与全连接神将网络一致。完整代码请参考：完整代码。

3.2 与全连接神经网络的比较

初始化模型，并打印该模型的参数总量：

# 初始化模型，并将模型移动到gpu
model = Model(next(iter(train_loader))[0]).to(device)
# 计算模型参数总量
total = sum([param.nelement() for param in model.parameters()])
print("Number of parameter: %.2fK" % (total/1e3))

Number of parameter: 3.33K

训练该网络与全连接神将网络，均只进行5个epoch的迭代，将两个模型的结果进行对比，各种对比数据如下：

网络	参数量	训练时长	测试准确率
全连接	109.39k	37.32s	78.68%
CNN	3.33k	36.95s	80.20%

尽管5个epoch两个模型都没有收敛，在准确率的对比上没有太大意义，但是我们依然可以注意到，CNN的网络参数仅是全连接网络的不到1/30，并且保持训练速度基本一致。

3.3 模型参数的可视化

我们在训练神经的过程中，常常会有这样的疑惑，经过若干次的迭代之后，网络模型每一层究竟学习到了什么内容？能不能直观地看到训练完成后的网络的参数？下面我们着手对CNN模型的第一层网络参数进行可视化。

要可视化模型的参数，我们可以这样思考：如果有这样一个输入$x$，将它送入网络，使得网络中某一个神经元的输出最大，那么这个输入$x$就是该神经元最“想看到”的输入，也就是该神经元要检测的内容。

按照上述思路，我们可以反过来，将CNN网络的参数视为定值，将输入x视为变量，利用反向传播算法，得到使得某个神经元输出最大的输入。下面给出可视化的代码：

import torch
from models.CNN_MNIST import Model
from torch.optim import SGD
import matplotlib.pyplot as plt


def visualize_loop(model, x, i, optimizer):
    # 定义损失函数为CNN模型第一层第i个神经元的输出值的和
    y = x
    for layer in model:
        y = layer(y)
    loss = -y[0, i].sum()+(y>0).type(torch.float).sum()
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    return loss


if __name__ == '__main__':
    # 读取模型参数
    model = torch.load("model_cnn_mnist.pth", map_location=torch.device('cpu'))
    # 取消模型自动求导
    model.requires_grad_(False)
    layers = [model.layer1, model.layer2, model.layer_fc]
    for i in range(1, len(layers)+1):
        figure = plt.figure(figsize=(8, 8))
        visual_xs = []
        layer = layers[:i]
        for idx in range([16, 8, 10][i-1]):
            # 初始化输入，并将其放到gpu上计算
            xs = torch.randn((1, 1, 28, 28))
            # 打开自动求导
            xs.requires_grad = True
            # 初始化优化器
            optimizer = SGD([xs], 0.05, momentum=0.5)
            for i in range(300):
                loss = visualize_loop(layer, xs, idx, optimizer)
            visual_xs.append(xs.cpu().detach().numpy()[0].reshape((28, 28)))
            figure.add_subplot(4, 4, idx+1)
            plt.title(f"No.{idx}-{loss.item():.2f}")
            plt.axis("off")
            plt.imshow(visual_xs[-1], cmap="gray")
        plt.show()